زمكان
| جزء من سلسلة عن |
| الزمكان |
|---|
 |
|
النسبية الخاصة النسبية العامة |

الزمكان (الزمان -مكان) Spacetime مصطلح حديث منحوت من كلمتي الزمان والمكان لتعبر عن الفضاء رباعي الأبعاد الذي أدخلته النظرية النسبية ليكون فضاء الحدث بدلاً من المكان المطلق الفارغ في نظرية الكم.
في هذا الفضاء الرباعي الأبعاد تميز كل نقطة برباعية (س,ع,ص,ز) حيث ترمز س,ع,ص إلى الاحداثيات المكانية و يرمز ز إلى الإحداثي الزمني.
فهو المزج بين الزمان و المكان في إطار واحد بحيث لا يتم الفصل بينهما عند إجراء الحسابات الفيزيائية.
ظهرت هذه الأطروحة بواسطة عالم الفيزياء ألبرت أينشتاين في نموذجه النسبي الخاص.
Introduction
تعريفات

التاريخ
An important example is Henri Poincaré,[1][2] who in 1898 argued that the simultaneity of two events is a matter of convention.[3][note 1] In 1900, he recognized that Lorentz's "local time" is actually what is indicated by moving clocks by applying an explicitly operational definition of clock synchronization assuming constant light speed.[note 2] In 1900 and 1904, he suggested the inherent undetectability of the aether by emphasizing the validity of what he called the principle of relativity, and in 1905/1906[4] he mathematically perfected Lorentz's theory of electrons in order to bring it into accordance with the postulate of relativity. While discussing various hypotheses on Lorentz invariant gravitation, he introduced the innovative concept of a 4-dimensional space-time by defining various four vectors, namely four-position, four-velocity, and four-force.[5][6] He did not pursue the 4-dimensional formalism in subsequent papers, however, stating that this line of research seemed to "entail great pain for limited profit", ultimately concluding "that three-dimensional language seems the best suited to the description of our world".[6] Furthermore, even as late as 1909, Poincaré continued to believe in the dynamical interpretation of the Lorentz transform.[7] For these and other reasons, most historians of science argue that Poincaré did not invent what is now called special relativity.[2][7]
When Einstein published in 1905, another of his competitors, his former mathematics professor Hermann Minkowski, had also arrived at most of the basic elements of special relativity. Max Born recounted a meeting he had made with Minkowski, seeking to be Minkowski's student/collaborator:[8]
I went to Cologne, met Minkowski and heard his celebrated lecture 'Space and Time' delivered on 2 September 1908. […] He told me later that it came to him as a great shock when Einstein published his paper in which the equivalence of the different local times of observers moving relative to each other was pronounced; for he had reached the same conclusions independently but did not publish them because he wished first to work out the mathematical structure in all its splendor. He never made a priority claim and always gave Einstein his full share in the great discovery.
Minkowski had been concerned with the state of electrodynamics after Michelson's disruptive experiments at least since the summer of 1905, when Minkowski and David Hilbert led an advanced seminar attended by notable physicists of the time to study the papers of Lorentz, Poincaré et al. However, it is not at all clear when Minkowski began to formulate the geometric formulation of special relativity that was to bear his name, or to which extent he was influenced by Poincaré's four-dimensional interpretation of the Lorentz transformation. Nor is it clear if he ever fully appreciated Einstein's critical contribution to the understanding of the Lorentz transformations, thinking of Einstein's work as being an extension of Lorentz's work.[9]
Spacetime in special relativity
Spacetime interval
In three-dimensions, the distance between two points can be defined using the Pythagorean theorem:
Although two viewers may measure the x,y, and z position of the two points using different coordinate systems, the distance between the points will be the same for both (assuming that they are measuring using the same units). The distance is "invariant".
Reference frames
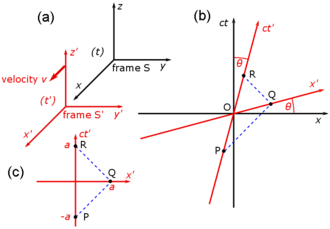
To gain insight in how spacetime coordinates measured by observers in different reference frames compare with each other, it is useful to work with a simplified setup with frames in a standard configuration. With care, this allows simplification of the math with no loss of generality in the conclusions that are reached. In Fig. 2‑2, two Galilean reference frames (i.e. conventional 3-space frames) are displayed in relative motion. Frame S belongs to a first observer O, and frame S′ (pronounced "S prime") belongs to a second observer O′.
- The x, y, z axes of frame S are oriented parallel to the respective primed axes of frame S′.
- Frame S′ moves in the x-direction of frame S with a constant velocity v as measured in frame S.
- The origins of frames S and S′ are coincident when time t = 0 for frame S and t′ = 0 for frame S′.[10]
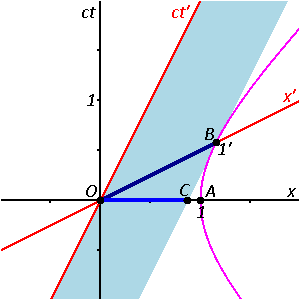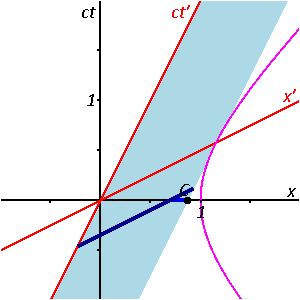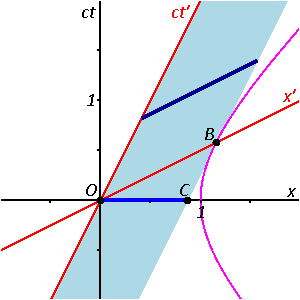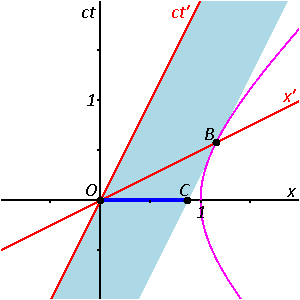
Fig. 2‑3a redraws Fig. 2‑2 in a different orientation. Fig. 2‑3b illustrates a spacetime diagram from the viewpoint of observer O. Since S and S′ are in standard configuration, their origins coincide at times t = 0 in frame S and t′ = 0 in frame S'. The ct′ axis passes through the events in frame S′ which have x′ = 0. But the points with x′ = 0 are moving in the x-direction of frame S with velocity v, so that they are not coincident with the ct axis at any time other than zero. Therefore, the ct′ axis is tilted with respect to the ct axis by an angle θ given by
The x′ axis is also tilted with respect to the x axis. To determine the angle of this tilt, we recall that the slope of the world line of a light pulse is always ±1. Fig. 2‑3c presents a spacetime diagram from the viewpoint of observer O′. Event P represents the emission of a light pulse at x′ = 0, ct′ = −a. The pulse is reflected from a mirror situated a distance a from the light source (event Q), and returns to the light source at x′ = 0, ct′ = a (event R).
The same events P, Q, R are plotted in Fig. 2‑3b in the frame of observer O. The light paths have slopes = 1 and −1 so that △PQR forms a right triangle. Since OP = OQ = OR, the angle between x′ and x must also be θ.[10]
While the rest frame has space and time axes that meet at right angles, the moving frame is drawn with axes that meet at an acute angle. The frames are actually equivalent. The asymmetry is due to unavoidable distortions in how spacetime coordinates can map onto a Cartesian plane, and should be considered no stranger than the manner in which, on a Mercator projection of the Earth, the relative sizes of land masses near the poles (Greenland and Antarctica) are highly exaggerated relative to land masses near the Equator.
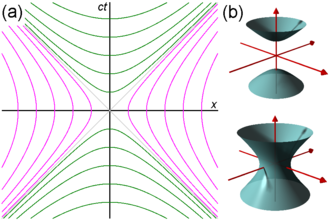
Light cone
Relativity of simultaneity
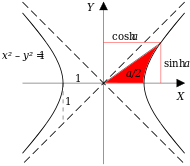
Invariant hyperbola
In Euclidean space (having spatial dimensions only), the set of points equidistant (using the Euclidean metric) from some point form a circle (in two dimensions) or a sphere (in three dimensions). In (1+1)-dimensional Minkowski spacetime (having one temporal and one spatial dimension), the points at some constant spacetime interval away from the origin (using the Minkowski metric) form curves given by the two equations
- with some positive real constant.
Time dilation and length contraction
Fig. 2-8 illustrates the invariant hyperbola for all events that can be reached from the origin in a proper time of 5 meters (approximately 1.67×10−8 s). Different world lines represent clocks moving at different speeds. A clock that is stationary with respect to the observer has a world line that is vertical, and the elapsed time measured by the observer is the same as the proper time. For a clock traveling at 0.3c, the elapsed time measured by the observer is 5.24 meters (1.75×10−8 s), while for a clock traveling at 0.7c, the elapsed time measured by the observer is 7.00 meters (2.34×10−8 s). This illustrates the phenomenon known as time dilation. Clocks that travel faster take longer (in the observer frame) to tick out the same amount of proper time, and they travel further along the x–axis than they would have without time dilation.[11] The measurement of time dilation by two observers in different inertial reference frames is mutual. If observer O measures the clocks of observer O′ as running slower in his frame, observer O′ in turn will measure the clocks of observer O as running slower.
Length contraction, like time dilation, is a manifestation of the relativity of simultaneity. Measurement of length requires measurement of the spacetime interval between two events that are simultaneous in one's frame of reference. But events that are simultaneous in one frame of reference are, in general, not simultaneous in other frames of reference.
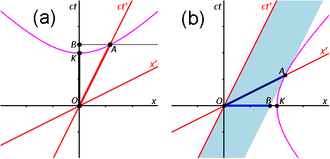
Mutual time dilation
Mutual time dilation and length contraction tend to strike beginners as inherently self-contradictory concepts. If an observer in frame S measures a clock, at rest in frame S', as running slower than his', while S' is moving at speed v in S, then the principle of relativity requires that an observer in frame S' likewise measures a clock in frame S, moving at speed −v in S', as running slower than hers. How two clocks can run both slower than the other, is an important question that "goes to the heart of understanding special relativity."[11]
Fig. 2-10 illustrates the previous discussion of mutual time dilation with Minkowski diagrams. The upper picture reflects the measurements as seen from frame S "at rest" with unprimed, rectangular axes, and frame S' "moving with v > 0", coordinatized by primed, oblique axes, slanted to the right; the lower picture shows frame S' "at rest" with primed, rectangular coordinates, and frame S "moving with −v < 0", with unprimed, oblique axes, slanted to the left.
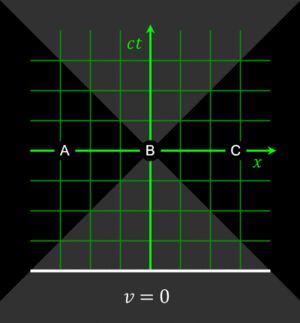
Each line drawn parallel to a spatial axis (x, x′) represents a line of simultaneity. All events on such a line have the same time value (ct, ct′). Likewise, each line drawn parallel to a temporal axis (ct, ct′) represents a line of equal spatial coordinate values (x, x′).
- One may designate in both pictures the origin O (= O′) as the event, where the respective "moving clock" is collocated with the "first clock at rest" in both comparisons. Obviously, for this event the readings on both clocks in both comparisons are zero. As a consequence, the worldlines of the moving clocks are the slanted to the right ct′-axis (upper pictures, clock W') and the slanted to the left ct-axes (lower pictures, clock W). The worldlines of W1 and W'1 are the corresponding vertical time axes (ct in the upper pictures, and ct′ in the lower pictures).
- In the upper picture the place for W2 is taken to be Ax > 0, and thus the worldline (not shown in the pictures) of this clock intersects the worldline of the moving clock (the ct′-axis) in the event labelled A, where "two clocks are simultaneously at one place". In the lower picture the place for W'2 is taken to be Cx′ < 0, and so in this measurement the moving clock W passes W'2 in the event C.
- In the upper picture the ct-coordinate At of the event A (the reading of W2) is labeled B, thus giving the elapsed time between the two events, measured with W1 and W2, as OB. For a comparison, the length of the time interval OA, measured with W', must be transformed to the scale of the ct-axis. This is done by the invariant hyperbola (see also Fig. 2-8) through A, connecting all events with the same spacetime interval from the origin as A. This yields the event C on the ct-axis, and obviously: OC < OB, the "moving" clock W' runs slower.
To show the mutual time dilation immediately in the upper picture, the event D may be constructed as the event at x′ = 0 (the location of clock W' in S'), that is simultaneous to C (OC has equal spacetime interval as OA) in S'. This shows that the time interval OD is longer than OA, showing that the "moving" clock runs slower.[10]
In the lower picture the frame S is moving with velocity -v in the frame S' at rest. The worldline of clock W is the ct-axis (slanted to the left), the worldline of W'1 is the vertical ct′-axis, and the worldline of W'2 is the vertical through event C, with ct′-coordinate D. The invariant parabola through event C scales the time interval OC to OA, which is shorter than OD; also, B is constructed (similar to D in the upper pictures) as simultaneous to A in S, at x = 0. The result OB > OC corresponds again to above.
The word "measure" is important. In classical physics an observer cannot affect an observed object, but the object's state of motion can affect the observer's observations of the object.
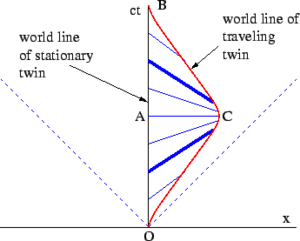
Twin paradox
Many introductions to special relativity illustrate the differences between Galilean relativity and special relativity by posing a series of "paradoxes". These paradoxes are, in fact, ill-posed problems, resulting from our unfamiliarity with velocities comparable to the speed of light. The remedy is to solve many problems in special relativity and to become familiar with its so-called counter-intuitive predictions. The geometrical approach to studying spacetime is considered one of the best methods for developing a modern intuition.[12]
Gravitation
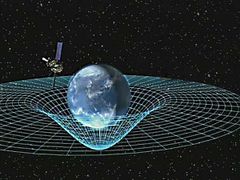
This introductory section has focused on the spacetime of special relativity, since it is the easiest to describe. Minkowski spacetime is flat, takes no account of gravity, is uniform throughout, and serves as nothing more than a static background for the events that take place in it. The presence of gravity greatly complicates the description of spacetime. In general relativity, spacetime is no longer a static background, but actively interacts with the physical systems that it contains. Spacetime curves in the presence of matter, can propagate waves, bends light, and exhibits a host of other phenomena.[11] A few of these phenomena are described in the later sections of this article.
Basic mathematics of spacetime
Galilean transformations
Relativistic composition of velocities
The composition of velocities is quite different in relativistic spacetime. To reduce the complexity of the equations slightly, we introduce a common shorthand for the ratio of the speed of an object relative to light,
Time dilation and length contraction revisited
Lorentz transformations
The Galilean transformations and their consequent commonsense law of addition of velocities work well in our ordinary low-speed world of planes, cars and balls. Beginning in the mid-1800s, however, sensitive scientific instrumentation began finding anomalies that did not fit well with the ordinary addition of velocities.
To transform the coordinates of an event from one frame to another in special relativity, we use the Lorentz transformations.
The Lorentz factor appears in the Lorentz transformations:
The inverse Lorentz transformations are:
When v ≪ c and x is small enough, the v2/c2 and vx/c2 terms approach zero, and the Lorentz transformations approximate to the Galilean transformations.
Deriving the Lorentz transformations
Energy and momentum
Extending momentum to four dimensions
Momentum of light
Total momentum
To understand how the Newtonian view of conservation of momentum needs to be modified in a relativistic context, we examine the problem of two colliding bodies limited to a single dimension.
Energy and momentum conservation
In a Newtonian analysis of interacting particles, transformation between frames is simple because all that is necessary is to apply the Galilean transformation to all velocities. Since , the momentum . If the total momentum of an interacting system of particles is observed to be conserved in one frame, it will likewise be observed to be conserved in any other frame.[13]
Newtonian momenta, calculated as , fail to behave properly under Lorentzian transformation. The linear transformation of velocities is replaced by the highly nonlinear so that a calculation demonstrating conservation of momentum in one frame will be invalid in other frames. Einstein was faced with either having to give up conservation of momentum, or to change the definition of momentum. As we have discussed in the previous section on four-momentum, this second option was what he chose.[14]
Beyond the basics
The topics in this section are of significantly greater technical difficulty than those in the preceding sections and are not essential for understanding Introduction to curved spacetime.
Rapidity
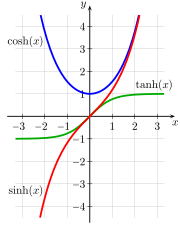
Lorentz transformations relate coordinates of events in one reference frame to those of another frame. Relativistic composition of velocities is used to add two velocities together. The formulas to perform the latter computations are nonlinear, making them more complex than the corresponding Galilean formulas.
This nonlinearity is an artifact of our choice of parameters.[15] We have previously noted that in an x–ct spacetime diagram, the points at some constant spacetime interval from the origin form an invariant hyperbola. We have also noted that the coordinate systems of two spacetime reference frames in standard configuration are hyperbolically rotated with respect to each other.
For the unit circle, the slope of the ray is given by
In the Cartesian plane, rotation of point (x, y) into point (x', y') by angle θ is given by
In a spacetime diagram, the velocity parameter is the analog of slope. The rapidity, φ, is defined by[13]
where
The rapidity defined above is very useful in special relativity because many expressions take on a considerably simpler form when expressed in terms of it. For example, rapidity is simply additive in the collinear velocity-addition formula;[15]
or in other words,
The Lorentz transformations take a simple form when expressed in terms of rapidity. The γ factor can be written as
Transformations describing relative motion with uniform velocity and without rotation of the space coordinate axes are called boosts.
Substituting γ and γβ into the transformations as previously presented and rewriting in matrix form, the Lorentz boost in the x direction may be written as
and the inverse Lorentz boost in the x direction may be written as
In other words, Lorentz boosts represent hyperbolic rotations in Minkowski spacetime.[13]
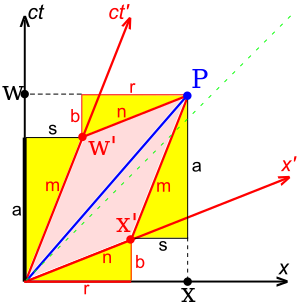
4‑vectors
Four‑vectors have been mentioned above in context of the energy-momentum 4‑vector, but without any great emphasis. Indeed, none of the elementary derivations of special relativity require them. But once understood, 4‑vectors, and more generally tensors, greatly simplify the mathematics and conceptual understanding of special relativity. Working exclusively with such objects leads to formulas that are manifestly relativistically invariant, which is a considerable advantage in non-trivial contexts. For instance, demonstrating relativistic invariance of Maxwell's equations in their usual form is not trivial, while it is merely a routine calculation (really no more than an observation) using the field strength tensor formulation. On the other hand, general relativity, from the outset, relies heavily on 4‑vectors, and more generally tensors, representing physically relevant entities. Relating these via equations that do not rely on specific coordinates requires tensors, capable of connecting such 4‑vectors even within a curved spacetime, and not just within a flat one as in special relativity. The study of tensors is outside the scope of this article, which provides only a basic discussion of spacetime.
Definition of 4-vectors
A 4-tuple, is a "4-vector" if its component A i transform between frames according to the Lorentz transformation.
If using coordinates, A is a 4–vector if it transforms (in the x-direction) according to
which comes from simply replacing ct with A0 and x with A1 in the earlier presentation of the Lorentz transformation.
As usual, when we write x, t, etc. we generally mean Δx, Δt etc.
The last three components of a 4–vector must be a standard vector in three-dimensional space. Therefore, a 4–vector must transform like under Lorentz transformations as well as rotations.[12]
Properties of 4-vectors
- Closure under linear combination: If A and B are 4-vectors, then is also a 4-vector.
- Inner-product invariance: If A and B are 4-vectors, then their inner product (scalar product) is invariant, i.e. their inner product is independent of the frame in which it is calculated. Note how the calculation of inner product differs from the calculation of the inner product of a 3-vector. In the following, and are 3-vectors:
- In addition to being invariant under Lorentz transformation, the above inner product is also invariant under rotation in 3-space.
- Two vectors are said to be orthogonal if Unlike the case with 3-vectors, orthogonal 4-vectors are not necessarily at right angles with each other. The rule is that two 4-vectors are orthogonal if they are offset by equal and opposite angles from the 45° line which is the world line of a light ray. This implies that a lightlike 4-vector is orthogonal with itself.
Examples of 4-vectors
- Displacement 4-vector: Otherwise known as the spacetime separation, this is (Δt, Δx, Δy, Δz), or for infinitesimal separations, (dt, dx, dy, dz).
- Velocity 4-vector: This results when the displacement 4-vector is divided by , where is the proper time between the two events that yield dt, dx, dy, and dz.
- The 4-velocity is tangent to the world line of a particle, and has a length equal to one unit of time in the frame of the particle.
- An accelerated particle does not have an inertial frame in which it is always at rest. However, as stated before in the earlier discussion of the transverse Doppler effect, an inertial frame can always be found which is momentarily comoving with the particle. This frame, the momentarily comoving reference frame (MCRF), enables application of special relativity to the analysis of accelerated particles.
Acceleration
In this section, we analyze several scenarios involving accelerated reference frames.
Dewan–Beran–Bell spaceship paradox
Introduction to curved spacetime
Basic propositions
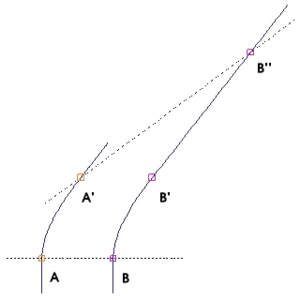
Newton's theories assumed that motion takes place against the backdrop of a rigid Euclidean reference frame that extends throughout all space and all time. Gravity is mediated by a mysterious force, acting instantaneously across a distance, whose actions are independent of the intervening space.[note 3] In contrast, Einstein denied that there is any background Euclidean reference frame that extends throughout space. Nor is there any such thing as a force of gravitation, only the structure of spacetime itself.[15]
In spacetime terms, the path of a satellite orbiting the Earth is not dictated by the distant influences of the Earth, Moon and Sun. Instead, the satellite moves through space only in response to local conditions. Since spacetime is everywhere locally flat when considered on a sufficiently small scale, the satellite is always following a straight line in its local inertial frame. We say that the satellite always follows along the path of a geodesic. No evidence of gravitation can be discovered following alongside the motions of a single particle.[15]
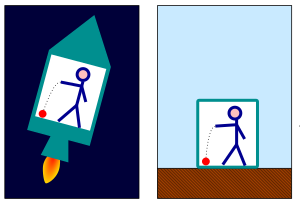
- The equivalence principle states that in any sufficiently small region of space, the effects of gravitation are the same as those from acceleration.
Instead, the focus in this section will be to explore a handful of elementary scenarios that serve to give somewhat of the flavor of general relativity.
Curvature of time
In the discussion of special relativity, forces played no more than a background role. Special relativity assumes the ability to define inertial frames that fill all of spacetime, all of whose clocks run at the same rate as the clock at the origin. Is this really possible? In a nonuniform gravitational field, experiment dictates that the answer is no. Gravitational fields make it impossible to construct a global inertial frame. In small enough regions of spacetime, local inertial frames are still possible. General relativity involves the systematic stitching together of these local frames into a more general picture of spacetime.[12]
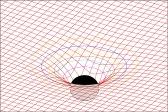
Curvature of space
The coefficient in front of describes the curvature of time in Newtonian gravitation, and this curvature completely accounts for all Newtonian gravitational effects. As expected, this correction factor is directly proportional to and , and because of the in the denominator, the correction factor increases as one approaches the gravitating body, meaning that time is curved.

Sources of spacetime curvature
In Newton's theory of gravitation, the only source of gravitational force is mass.
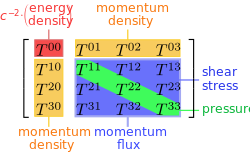
Energy-momentum
Pressure and stress
Quantities that are directly related to energy and momentum should be sources of gravity as well, namely internal pressure and stress. Taken together, mass-energy, momentum, pressure and stress all serve as sources of gravity: Collectively, they are what tells spacetime how to curve.
In general relativity,
- The equality of and is dictated by the equivalence principle.
- There is no "action and reaction" principle dictating any necessary relationship between and .[16]
• Pressure as a gravitational source
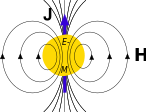
• Gravitomagnetism
The existence of gravitomagnetism was proven by Gravity Probe B (GP-B), a satellite-based mission which launched on 20 April 2004.[17] The spaceflight phase lasted until . The mission aim was to measure spacetime curvature near Earth, with particular emphasis on gravitomagnetism.
Technical topics
Is spacetime really curved?
In Poincaré's conventionalist views, the essential criteria according to which one should select a Euclidean versus non-Euclidean geometry would be economy and simplicity. A realist would say that Einstein discovered spacetime to be non-Euclidean. A conventionalist would say that Einstein merely found it more convenient to use non-Euclidean geometry. The conventionalist would maintain that Einstein's analysis said nothing about what the geometry of spacetime really is.[18]
Such being said,
- 1. Is it possible to represent general relativity in terms of flat spacetime?
- 2. Are there any situations where a flat spacetime interpretation of general relativity may be more convenient than the usual curved spacetime interpretation?
Riemannian geometry
Curved manifolds
Privileged character of 3+1 spacetime
انظر أيضاً
- Basic introduction to the mathematics of curved spacetime
- Complex spacetime
- Einstein's thought experiments
- Global spacetime structure
- Metric space
- Philosophy of space and time
- Present
ملاحظات
- ^ By stating that simultaneity is a matter of convention, Poincaré meant that to talk about time at all, one must have synchronized clocks, and the synchronization of clocks must be established by a specified, operational procedure (convention). This stance represented a fundamental philosophical break from Newton, who conceived of an absolute, true time that was independent of the workings of the inaccurate clocks of his day. This stance also represented a direct attack against the influential philosopher Henri Bergson, who argued that time, simultaneity, and duration were matters of intuitive understanding.[3]
- ^ The operational procedure adopted by Poincaré was essentially identical to what is known as Einstein synchronization, even though a variant of it was already a widely used procedure by telegraphers in the middle 19th century. Basically, to synchronize two clocks, one flashes a light signal from one to the other, and adjusts for the time that the flash takes to arrive.[3]
- ^ Newton himself was acutely aware of the inherent difficulties with these assumptions, but as a practical matter, making these assumptions was the only way that he could make progress. In 1692, he wrote to his friend Richard Bentley: "That Gravity should be innate, inherent and essential to Matter, so that one body may act upon another at a distance thro' a Vacuum, without the Mediation of any thing else, by and through which their Action and Force may be conveyed from one to another, is to me so great an Absurdity that I believe no Man who has in philosophical Matters a competent Faculty of thinking can ever fall into it."
تفاصيل اضافية
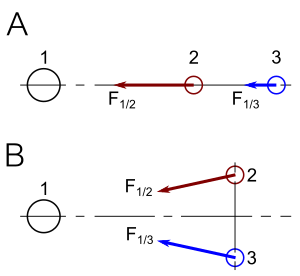
- ^ Different reporters viewing the scenarios presented in this figure interpret the scenarios differently depending on their knowledge of the situation. (i) A first reporter, at the center of mass of particles 2 and 3 but unaware of the large mass 1, concludes that a force of repulsion exists between the particles in scenario A while a force of attraction exists between the particles in scenario B. (ii) A second reporter, aware of the large mass 1, smiles at the first reporter's naiveté. This second reporter knows that in reality, the apparent forces between particles 2 and 3 really represent tidal effects resulting from their differential attraction by mass 1. (iii) A third reporter, trained in general relativity, knows that there are, in fact, no forces at all acting between the three objects. Rather, all three objects move along geodesics in spacetime.
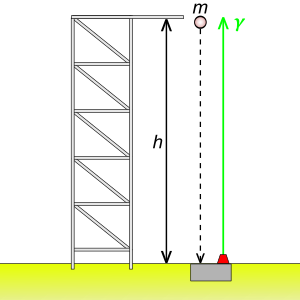
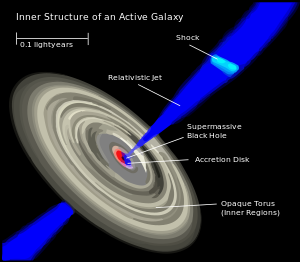
- ^ Relativistic jets are beams of ionised matter accelerated close to the speed of light. Most have been observationally associated with central black holes of some active galaxies, radio galaxies or quasars, as well as stellar black holes, neutron stars and pulsars. Beam lengths may extend from several thousand to millions of parsecs.
المراجع
- ^ Darrigol, O. (2005), "The Genesis of the theory of relativity", Séminaire Poincaré 1: 1–22, doi:, ISBN 978-3-7643-7435-8, Bibcode: 2006eins.book....1D, http://www.bourbaphy.fr/darrigol2.pdf
- ^ أ ب Miller, Arthur I. (1998). Albert Einstein's Special Theory of Relativity. New York: Springer-Verlag. ISBN 0387948708.
- ^ أ ب ت Galison, Peter (2003). Einstein's Clocks, Poincaré's Maps: Empires of Time. New York: W. W. Norton & Company, Inc. pp. 13–47. ISBN 0393020010.
- ^ Poincare, Henri (1906). "On the Dynamics of the Electron (Sur la dynamique de l'électron)". Rendiconti del Circolo Matematico di Palermo. 21: 129–176. Bibcode:1906RCMP...21..129P. doi:10.1007/bf03013466. hdl:2027/uiug.30112063899089. Retrieved 15 July 2017.
- ^ Zahar, Elie (1989), "Poincaré's Independent Discovery of the relativity principle", Einstein's Revolution: A Study in Heuristic, Chicago: Open Court Publishing Company, ISBN 0-8126-9067-2
- ^ أ ب Walter, Scott A. (2007). "Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910". In Renn, Jürgen; Schemmel, Matthias (eds.). The Genesis of General Relativity, Volume 3. Berlin: Springer. pp. 193–252. Archived from the original on 15 July 2017. Retrieved 15 July 2017.
- ^ أ ب خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةPais - ^ قالب:Cite arxiv
- ^ Galison, Peter Louis (1979). "Minkowski's space-time: From visual thinking to the absolute world". Historical Studies in the Physical Sciences. 10: 85–121. doi:10.2307/27757388. JSTOR 27757388.
- ^ أ ب ت Collier, Peter (2017). A Most Incomprehensible Thing: Notes Towards a Very Gentle Introduction to the Mathematics of Relativity (3rd ed.). Incomprehensible Books. ISBN 9780957389465.
- ^ أ ب ت خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةSchutz - ^ أ ب ت Schutz, Bernard F. (1985). A first course in general relativity. Cambridge, UK: Cambridge University Press. p. 26. ISBN 0521277035.
- ^ أ ب ت خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةMorin - ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةBais - ^ أ ب ت ث خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةTaylor - ^ Bondi, Hermann (1957). DeWitt, Cecile M.; Rickles, Dean (eds.). The Role of Gravitation in Physics: Report from the 1957 Chapel Hill Conference. Berlin: Max Planck Research Library. pp. 159–162. ISBN 9783869319636. Retrieved 1 July 2017.
- ^ "Gravity Probe B: FAQ". Retrieved 2 July 2017.
- ^ Murzi, Mauro. "Jules Henri Poincaré (1854–1912)". Internet Encyclopedia of Philosophy (ISSN 2161-0002). Retrieved 9 April 2018.
للاستزادة
- قالب:BarrowTipler1986
- George F. Ellis and Ruth M. Williams (1992) Flat and curved space–times. Oxford Univ. Press. ISBN 0-19-851164-7
- Lorentz, H. A., Einstein, Albert, Minkowski, Hermann, and Weyl, Hermann (1952) The Principle of Relativity: A Collection of Original Memoirs. Dover.
- Lucas, John Randolph (1973) A Treatise on Time and Space. London: Methuen.
- Penrose, Roger (2004). The Road to Reality. Oxford: Oxford University Press. ISBN 0-679-45443-8. Chpts. 17–18.
- Taylor, E. F.; Wheeler, John A. (1992). Spacetime Physics, Second Edition. Internet Archive: W. H. Freeman. ISBN 0-7167-2327-1.
وصلات خارجية
- Albert Einstein on space-time 13th edition Encyclopædia Britannica Historical: Albert Einstein's 1926 article
- Encyclopedia of Space-time and gravitation Scholarpedia Expert articles
- Stanford Encyclopedia of Philosophy: "Space and Time: Inertial Frames" by Robert DiSalle.