فضاء سباعي الأبعاد
في الفيزياء والرياضيات, a تسلسل الأرقام ر يمكن أن يفهم أيضا على أنه موقع في فضاء أبعاد ر. عندما ر = 7، تسمى كل مجموعة من هذه المواقع فضاء إقليدي سباعي الأبعاد. Often such a space is studied as a vector space, without any notion of distance. Seven-dimensional Euclidean space is seven-dimensional space equipped with a Euclidean metric, which is defined by the dot product.
More generally, the term may refer to a seven-dimensional vector space over any field, such as a seven-dimensional complex vector space, which has 14 real dimensions. It may also refer to a seven-dimensional manifold such as a 7-sphere, or a variety of other geometric constructions.
Seven-dimensional spaces have a number of special properties, many of them related to the octonions. An especially distinctive property is that a cross product can be defined only in three or seven dimensions. This is related to Hurwitz's theorem, which prohibits the existence of algebraic structures like the quaternions and octonions in dimensions other than 2, 4, and 8. The first exotic spheres ever discovered were seven-dimensional.
الهندسة
7-polytope
A polytope in seven dimensions is called a 7-polytope. The most studied are the regular polytopes, of which there are only three in seven dimensions: the 7-simplex, 7-cube, and 7-orthoplex. A wider family are the uniform 7-polytopes, constructed from fundamental symmetry domains of reflection, each domain defined by a Coxeter group. Each uniform polytope is defined by a ringed Coxeter-Dynkin diagram. The 7-demicube is a unique polytope from the D7 family, and 321, 231, and 132 polytopes from the E7 family.
| A6 | B7 | D7 | E7 | |||
|---|---|---|---|---|---|---|
 7-simplex {3,3,3,3,3,3} |
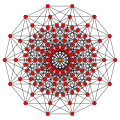 7-cube {4,3,3,3,3,3} |
 7-orthoplex {3,3,3,3,3,4} |
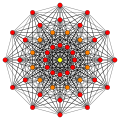 7-demicube h{4,3,3,3,3,3} = {3,34,1} |
 321 {3,3,3,32,1} |
 231 {3,3,33,1} |
 132 {3,33,2} |
6-كرة
The 6-sphere or hypersphere in seven-dimensional Euclidean space is the six-dimensional surface equidistant from a point, e.g. the origin. It has symbol S6, with formal definition for the 6-sphere with radius r of
The volume of the space bounded by this 6-sphere is
which is 4.72477 × r7, or 0.0369 of the 7-cube that contains the 6-sphere
التطبيقات
الفيزياء
جداء تقاطعي
الجداء التقاطعي، الذي هو حاصل ضرب ذو قيمة متجهية، ثنائي الخطية، لاتبديلي ومتعامد لمتجهين، مـُعرَّف في سبعة أبعاد. إلى جانب الجداء التقاطعي الأكثر شيوعاً في ثلاثة أبعاد، فهو حاصل الضرب الوحيد من هذا القبيل، ماعدا الجداءات التافهة.
Exotic spheres
In 1956, John Milnor constructed an exotic sphere in 7 dimensions and showed that there are at least 7 differentiable structures on the 7-sphere. In 1963 he showed that the exact number of such structures is 28.
انظر أيضا
- Euclidean space
- Euclidean geometry
- 7-polytope
- Polytope
- M-theory
- List of geometry topics
- List of regular polytopes
- Exotic sphere



