فضاء متجه
الفضاء المتجه (والذي يُسمى أيضاً الفضاء الخطي) هو مجموعة أدوات تسمى متجهات، والتي قد تكون مضافة معاً و مضروبة (مقاسة) بالأرقام، تسمى مقاسات. غالباً ما يتم أخذ المقاييس على أنها أعداد حقيقية، ولكن هناك أيضاً فضاءات متجهة مع مضاعفة عددية بواسطة الأعداد العقدية، الأعداد الكسرية، أو بشكل عام أي مجال. يجب أن تفي عمليات جمع المتجه والضرب العددي بمتطلبات معينة، تسمى متجهات البديهيات (المدرجة أدناه في § التعريف). لتحديد أن العدديات هي أرقام حقيقية أو عقدية، غالباً ما يتم استخدام المصطلحين فضاء المتجه الحقيقي و فضاء المتجه العقدي.
توجد مجموعات معينة من المتجهات الإقليدية وهي أمثلة شائعة لفضاء المتجه. وهي تمثل فيزيائياً كميات مثل القوى، حيث يمكن إضافة أي قوتين (من نفس النوع) للحصول على قوة ثالثة، وضرب متجهات القوى في المضاعف الحقيقي هو متجه قوة آخر. على نفس المنوال (ولكن بمعنى هندسي أكثر)، فإن المتجهات التي تمثل الإزاحة في المستوى أو الفضاء ثلاثي الأبعاد تشكل أيضاً فضاءات متجهة. لا يجب بالضرورة أن تكون المتجهات في فضاءات المتجهات أدوات تشبه الأسهم كما تظهر في الأمثلة المذكورة: يتم اعتبار المتجهات على أنها أدوات رياضياتية مجردة لها خصائص معينة، والتي يمكن تصورها في بعض الحالات على أنها أسهم.
فضاءات المتجهات هي موضوع الجبر الخطي وتتميز بـ بالبعد إلى حد بعيد، والتي، بشكل تقريبي، تحدد عدد الاتجاهات المستقلة في الفضاء. تنشأ الفضاءات المتجهية اللانهائية الأبعاد بشكل طبيعي في التحليل الرياضي مثل فضاء الدالة، والتي تكون متجهاتها عبارة عن دوال. تُزود هذه الفضاءات المتجهة عموماً ببعض الهياكل الإضافية مثل الطوبولوجيا، والتي تسمح بالنظر في قضايا التقريب و الاستمرارية. من بين هذه الهياكل، تلك التي تم تحديدها بواسطة معيار أو الجداء الداخلي الأكثر شيوعاً (كونها مجهزة بمفهوم المسافة بين متجهين). فهذه هي حالة فضاء باناخ و فضاء هلبرت، والتي تعتبر أساسية في التحليل الرياضي.
تاريخياً، يمكن تتبع الأفكار الأولى التي أدت إلى الفضاءات المتجهة إلى الهندسة التحليلية الخاصة بالقرن السابع عشر، المصفوفات، وأنظمة المعادلات الخطية والمتجهات الإقليدية. المعالجة الحديثة الأكثر تجريدية، التي صاغها لأول مرة گوزيپي پينو في عام 1888، تشمل أدوات أكثر عمومية من الفضاء الإقليدي، ولكن يمكن اعتبار الكثير من النظرية امتداداً لأفكار هندسية كلاسيكية مثل الخطوط، المستويات ونظائرها ذات الأبعاد الأعلى.
اليوم، يتم تطبيق الفضاءات المتجهة في جميع أنحاء الرياضيات و العلوم و الهندسة. إنها الفكرة الجبرية الخطية المناسبة للتعامل مع أنظمة المعادلات الخطية. إنها توفر إطار عمل لـ منشور فورييه، الذي يتم استخدامه في إجراءات ضغط الصورة، كما أنها توفر بيئة يمكن استخدامها لتقنيات الحل لـ المعادلات التفاضلية الجزئية. علاوة على ذلك، توفر فضاءات المتجهات طريقة مجردة خال الإحداثيات للتعامل مع الأشياء الهندسية والفيزيائية مثل موترات. وهذا بدوره يسمح بفحص الخصائص المحلية لـ الطيات بواسطة تقنيات الخطية. يمكن تعميم الفضاءات المتجهة بعدة طرق، مما يؤدي إلى مفاهيم أكثر تقدماً في الهندسة و الجبر المجرد.
| البنى الجبرية |
|---|
مقدمة وتعريف
سيتم شرح مفهوم الفضاء المتجه أولاً من خلال وصف مثالين معينين:
المثال الأول: الأسهم في المستوي
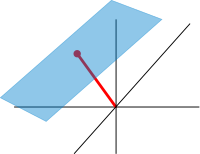
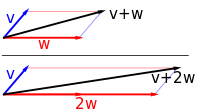
يتكون المثال الأول لفضاء المتجه من سهم في مستوى، بدءاً من نقطة ثابتة واحدة. يستخدم هذا في الفيزياء لوصف القوى أو السرعات. بالنظر إلى أي سهمين من هذا القبي ، v و w، فإن متوازي الأضلاع الممتد بهذين السهمين يحتوي على سهم قطري واحد يبدأ من الأصل أيضاً. يسمى هذا السهم الجديد مجموع السهمين، ويشار إليه v + w.[1]في الحالة الخاصة لسهمين على نفس الخط، يكون مجموعهما هو السهم الموجود على هذا الخط الذي يكون طوله هو مجموع أو فرق الأطوال، اعتماداً على ما إذا كان السهمان لهما نفس الاتجاه. عملية أخرى يمكن إجراؤها باستخدام الأسهم هي القياس: بالنظر إلى أي رقم حقيقي موجب a، السهم الذي له نفس اتجاه v، ولكنه يتوسع أو يتقلص بضرب طوله في a، ويسمى بضرب v بـ a. يتم الإشارة إليه av عندما يكون a سالب، يتم تعريف av على أنه سهم يشير في الاتجاه المعاكس بدلاً من ذلك.
فيما يلي بعض الأمثلة: إذا كان a = 2، فإن المتجه الناتج aw له نفس اتجاه w، لكنه امتد إلى الطول المضاعف لـ w (الصورة اليمنى أدناه). بشكل مكافئ، 2w هو المجموع w + w. علاوة على ذلك، (−1)v = −v لها الاتجاه المعاكس ونفس الطول مثل v (متجه أزرق يشير لأسفل في الصورة اليمنى).

|
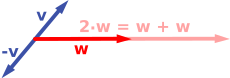
|
المثال الثاني: أزواج أرقام مرتبية
يتم توفير مثال رئيسي ثانٍ لفضاء المتجه بواسطة أزواج من الأرقام الحقيقية x و y. (يعتبر ترتيب المكونات x و y مهماً، لذلك يُطلق على هذا الزوج أيضاً باسم الزوج المرتبي.) الزوج مكتوب كـ (x, y). يتم تحديد مجموع اثنين من هذه الأزواج وضرب الزوج برقم على النحو التالي:
و
.
يختصر المثال الأول أعلاه إلى هذا المثال، إذا تم تمثيل الأسهم بواسطة زوج الإحداثيات الديكارتية لنقاط النهاية الخاصة بهم.
تعريف
في هذه المقالة، يتم تمثيل المتجهات بخط عريض لتمييزها عن العددية.[nb 1]
فضاء المتجه على المجال F هي مجموعة V جنباً إلى جنب مع عمليتين تحقق ثماني مسلمات مدرجة أدناه. يشير في ما يلي، V × V إلى الجداء الديكارتي لـ V مع نفسه و تشير → إلى تعيين من مجموعة إلى أخرى.
- تسمى العملية الأولى إضافة متجه أو ببساطة إضافة + : V × V → V، يأخذ أي متجهين v و w ويخصص لهم متجهاً ثالثاً والذي يتم كتابته بشكل شائع كـ v + w، ويسمى مجموع هذين المتجهين. (المتجه الناتج هو أيضاً عنصر من عناصر المجموعة V.)
- تسمى العملية الثانية، الضرب العددي · : F × V → V تأخذ أي عددية a وأي متجه v ويعطي متجهاً آخر av. (وبالمثل، فإن المتجه av هو عنصر من عناصر المجموعة V. يجب عدم الخلط بين الضرب العددي و الجداء العددي، يُطلق عليه أيضاً الجداء الداخلي أو الجداء النقطي، وهو عبارة عن بنية إضافية موجودة في بعض الفضاءات المتجهية المحددة، ولكن ليس جميعها. الضرب العددي هو مضاعفة متجه بواسطة عددي؛ الآخر هو مضاعفة متجهين ينتج عدداً.)
يطلق على عناصر V اسم المتجهات. يُطلق على عناصر F اسم العدديات. تشمل الرموز الشائعة للدلالة على الفضاءات المتجهة , و .[1]
في المثالين أعلاه، المجال هو حقل الأرقام الحقيقية، وتتكون مجموعة المتجهات من الأسهم المستوية بنقطة بداية ثابتة وأزواج من الأرقام الحقيقية، على التوالي.
لكي يكون فضاء متجه، يجب أن تلتزم المجموعة V وعمليات الجمع والضرب بعدد من المتطلبات تسمى البديهيات.[2]تم سردها في الجدول أدناه، حيث u و v و w تشير إلى متجهات عشوائية في V، و a و b تشير إلى العدديات في F.[3][4]
| المُسلَّمة | المعنى |
|---|---|
| تجميعية الإضافة | u + (v + w) = (u + v) + w |
| تبديلية الإضافة | u + v = v + u |
| عنصر مطابقة الإضافة | يوجد عنصر 0 ∈ V، يسمى المتجه الصفري، مثل v + 0 = v لكل v ∈ V. |
| عناصر معكوسة للإضافة | لكل v ∈ V، يوجد عنصر −v ∈ V، يسمى معكوس مضاف لـ v, مثل v + (−v) = 0. |
| التطابقية في الضرب العددي مع الضرب المجالي | a(bv) = (ab)v [nb 2] |
| عنصر مطابقة الضرب العددي | 1v = v، حيث يشير 1 إلى مطابقة مضاعفة في F. |
| توزيع الضرب العددي بالنسبة إلى إضافة المتجهات | a(u + v) = au + av |
| توزيعية الضرب العددي فيما يتعلق بالجمع المجالي | (a + b)v = av + bv |
هذه البديهيات تعمم خصائص المتجهات المقدمة في الأمثلة أعلاه. في الواقع، لا تعتمد نتيجة إضافة زوجين مرتبيين (كما في المثال الثاني أعلاه) على ترتيب المجموعات:
- (xv, yv) + (xw, yw) = (xw, yw) + (xv, yv).
وبالمثل، في المثال الهندسي للمتجهات كسهم، {v + w = w + v نظراً لأن متوازي الأضلاع الذي يحدد مجموع المتجهات مستقل عن ترتيب المتجهات. يمكن التحقق من جميع البديهيات الأخرى بطريقة مماثلة في كلا المثالين. وهكذا، من خلال تجاهل الطبيعة الملموسة لنوع معين من المتجهات، فإن التعريف يدمج هذين المثالين والعديد من الأمثلة الأخرى في مفهوم واحد عن الفضاء المتجه.
يمكن تعريف طرح متجهين والقسمة على عدد (غير صفري) على أنه
- .
عندما يكون المجال العددي F هو الأعداد الحقيقية R، يُطلق على فضاء المتجه فضاء المتجه الحقيقي. عندما يكون المجال العددي هو الأعداد العقدية C، فإن فضاء المتجه تسمى فضاء المتجه العقدي. هاتان الحالتان هما الأكثر استخداماً في الهندسة. يسمح التعريف العام لفضاء المتجه بأن تكون العدديات عناصر لأي مجال F ثابت. تُعرف الفكرة بعد ذلك باسم F - فضاء متجه أو فضاء متجه على F. المجال، في الأساس، هو مجموعة من الأرقام التي تمتلك عمليات إضافة و طرح و ضرب و قسمة.[nb 3] على سبيل المثال، تشكل الأعداد الكسرية مجالاً.
على عكس الحدس الناجم عن المتجهات في المستوى والحالات ذات الأبعاد الأعلى، في الفضاءات المتجهة العامة، لا يوجد مفهوم المقاربة، الزاويا أو المسافات. للتعامل مع مثل هذه الأمور، يتم تقديم أنواع معينة من الفضاءات المتجهة؛ راجع § فضاءات المتجهات ذات البنية الإضافية أدناه للحصول على المزيد.
الصيغ البديلة والنتائج الأولية
إضافة المتجه والضرب العددي هما عمليتان تحققان خاصية الإغلاق: u + v و av في V لكل a في F, و u, v في V. تذكر بعض المصادر القديمة هذه الخصائص كبديهيات منفصلة.[5]
بأسلوب الجبر المجرد، تكافئ البديهيات الأربع الأولى المطالبة بأن تكون مجموعة المتجهات مجموعة أبيلية تحت الإضافة. تعطي البديهيات المتبقية هذه المجموعة بنية وحدة-F. بمعنى آخر، هناك حلقة تماثل f من المجال F في حلقة التشابه من مجموعة متجهية. ثم يتم تعريف av على أنه (f(a))(v).[6]
هناك عدد من النتائج المباشرة لبديهيات الفضاء المتجه. بعضها مشتق من نظرية المجموعة الابتدائية، المطبقة على مجموعة المتجهات المضافة: على سبيل المثال، يكون المتجه الصفري 0 لـ V والمعكوس الجمعي −v لأي متجه v فريدان. يتبع المزيد من الخصائص من خلال توظيف قانون التوزيع أيضاً في الضرب العددي، على سبيل المثال av يساوي 0 إذا و فقط إذا كانت a تساوي 0 أو v تساوي 0.
تاريخ
تنبع الفضاءات المتجهة من الهندسة التآلفية، عن طريق إدخال الإحداثيات في المستوي أو الفضاء ثلاثي الأبعاد. حوالي عام 1636، أسس علماء الرياضيات الفرنسيون رينيه ديكارت و پيير دي فيرما الهندسة التحليلية من خلال تحديد حلول لمعادلة من متغيرين بنقاط على منحنى مستوي.[7]لتحقيق حلول هندسية بدون استخدام الإحداثيات، أدخل بولزانو، في عام 1804، عمليات معينة على النقاط والخطوط والمستويات، والتي سبقت المتجهات.[8]تم استخدام هذا العمل في مفهوم الإحداثيات المركزية بواسطة موبيوس في عام 1827.[9]فقد كانت أساس تعريف المتجهات هو فكرة بيلاڤيتيس عن النقطة الثنائية، وهي جزء موجه واحد من نهاياته فهو الأصل والآخر هدف. تم إعادة النظر في المتجهات مع تقديم الأعداد العقدية بواسطة أرگاند و هاملتون وابتداء الرباعية بواسطة الأخير.[10]إنها عناصر في R2 و R4; ترجع معاملتها باستخدام تركيبة خطية إلى لاگير في عام 1867، الذي قام أيضًا بتعريف أنظمة المعادلات الخطية.
في عام 1857، قام كايلي بتقديم ترميز المصفوفة الذي يسمح بمواءمة وتبسيط المخططات الخطية. في نفس الوقت تقريباً، درس گراسمان حساب التفاضل والتكامل ثنائي المحور الذي بدأه موبيوس. لقد تصور مجموعات من الأشياء المجردة التي تتمتع بالعمليات.[11] في عمله، توجد مفاهيم الاستقلال الخطي و البعد، وكذلك الجداءات العددية. في الواقع، يتجاوز عمل گراسمان لعام 1844 إطار الفضاءات المتجهية، بأخذ الضرب بعين الاعتبار أيضاً، قاده إلى ما يسمى اليوم الجبر. كان عالم الرياضيات الإيطالي پينو أول من أعطى التعريف الحديث للفضاءات المتجهة والمخططات الخطية في عام 1888.[12]
يرجع التطور المهم لفضاءات المتجهات إلى بناء فضاءات الدالة بواسطة هنري ليبيسگ. تم إضفاء الطابع الاصطلاحي على هذا لاحقاً من قبل باناخ و هلبرت، حوالي عام 1920.[13]في ذلك الوقت، بدأ الجبر والمجال الجديد للتحليل الدالي بالتفاعل، لا سيما مع المفاهيم الأساسية مثل فضاءات p - دوال قابلة للتكامل و فضاءات هلبرت.[14]في هذا الوقت أيضاً، تم إجراء الدراسات الأولى المتعلقة بالفضاءات المتجهية اللانهائية.
أمثلة
الفضاء الإحداثي
أبسط مثال على فضاء متجه على مجال F هو المجال نفسه، المجهز بجمعه وضربه القياسيين. بشكل عام، كل n-مجموعات عناصر (تسلسلات بطول n)
- (a1, a2, ..., an)
من عناصر F تشكل فضاء متجه يُشار إليها عادةً بـ Fn وتسمى الفضاء الإحداثي.[15] الحالة n = 1 هي أبسط مثال مذكور أعلاه، حيث يُنظر أيضاً إلى المجال F على أنه فضاء متجه على نفسه. تمت مناقشة الحالة F = R و n = 2 في المقدمة أعلاه.
الأعداد العقدية ومنشورات المجالات الأخرى
مجموعة الأعداد العقدية C، أي الأرقام التي يمكن كتابتها بالصيغة x + iy لـ الأعداد الحقيقية x و y حيث i هي وحدة تخيلية، شكّل فضاء المتجه على القيم الحقيقية مع الجمع والضرب المعتاد: (x + iy) + (a + ib) = (x + a) + i(y + b) و c ⋅ (x + iy) = (c ⋅ x) + i(c ⋅ y) للأعداد الحقيقية x, y, a, b و c. تنبع البديهيات المختلفة لفضاء المتجه من حقيقة أن نفس القواعد تنطبق على حساب العدد المركب.
في الواقع، فإن مثال الأعداد العقدية هو نفسه في الأساس (أي أنه متماثل) في فضاء المتجه للأزواج المرتبة من الأعداد الحقيقية المذكورة أعلاه: إذا فكرنا في العدد العقدي x + i y يمثل الزوج المرتب (x, y) في المستوى العقدي ثم نحن لاحظ أن قواعد الجمع والضرب القياسي تتوافق تماماً مع تلك الموجودة في المثال السابق.
بشكل أكثر عمومية، يقدم منشور المجال فئة أخرى من أمثلة الفضاءات المتجهة، لا سيما في الجبر و نظرية الأعداد الجبرية: مجال F الذي يحتوي على أصغر مجال E هو E - فضاء متجه، من خلال عمليات الضرب والإضافة المحددة لـF.[16]على سبيل المثال، الأرقام العقدية عبارة عن فضاء متجهي على R، ومنشور المجال هو فضاء متجه على Q..
فضاءات الدالة
تشكل الدوال من أي مجموعة ثابتة Ω إلى مجال F أيضاً فضاءات متجهة، عن طريق إجراء عمليات الجمع والضرب العددي النقطي. أي أن مجموع الدالتين f و g هو الدالة (f + g) المعطاة بواسطة
- (f + g)(w) = f(w) + g(w),
وبالمثل للضرب. تحدث فضاءات الدوال هذه في العديد من المواقف الهندسية، عندما تكون Ω هي الخط الحقيقي أو الفاصل الزمني ، أو مجموعة فرعية أخرى من R. العديد من المفاهيم في الطوبولوجيا والتحليل، مثل الاستمرارية، التكامل أو التفاضل حسنة السلوك فيما يتعلق بالخطية: المجاميع والمضاعفات العددية للدوال التي تمتلك مثل هذه الخاصية لا يزال لديهم تلك الخصائص.[17] لذلك، فإن مجموعة هذه الدوال هي فضاءات متجهة. تمت دراستها بمزيد من التفصيل باستخدام طرق التحليل الدالي، راجع أدناه.قالب:Huh تؤدي القيود الجبرية أيضاً إلى فضاءات متجهة: يتم إعطاء مسافة متجه F[x] بواسطة دوال متعددة الحدود:
المعادلات الخطية
ترتبط نظم المعادلات الخطية المتجانسة ارتباطاً وثيقاً بالفضاءات المتجهة.[19] على سبيل المثال، حلول
a + 3b + c = 0 4a + 2b + 2c = 0
مُعطاة بثلاثيات مع a و b = a/2 و c = −5a/2. إنها تشكل فضاء متجه: لا تزال المجاميع والمضاعفات العددية لمثل هذه الثلاثيات تحقق نفس نسب المتغيرات الثلاثة؛ وبالتالي فهي حلول أيضاً. يمكن استخدام المصفوفات لتكثيف المعادلات الخطية المتعددة على النحو الوارد أعلاه في معادلة متجهات واحدة، وهي
- Ax = 0,
حيث تكون A = هي المصفوفة التي تحتوي على معاملات المعادلات المحددة، x هو المتجه (a, b, c), Ax تشير إلى جداء المصفوفة، و 0 = (0, 0) هو المتجه الصفري. على نفس المنوال، فإن حلول المعادلات التفاضلية الخطية المتجانسة تشكل فضاءات متجهة. فمثلا،:f′′(x) + 2f′(x) + f(x) = 0 تعود f(x) = a e−x + bx e−x, حيث تكون a و b ثوابت عشوائية و ex هي دالة أسية طبيعية.
الأساس والأبعاد
يسمح الأساسللقواعد بتمثيل المتجهات بواسطة متسلسلة من الععديات تسمى إحداثيات أو مكونات. الأساس هو مجموعة (محدودة أو غير محدودة) B = {bi}i ∈ I من المتجهات bi، للملاءمة غالباً ما تتم فهرستها بواسطة بعض مجموعة فهرس I، الذي يمتد على كامل الفضاء وهو مستقل خطياً. يعني نشر الفضاء بكامله أن أي متجه v يمكن التعبير عنه كمجموع محدود (يسمى تركيبة خطية) لعناصر الأساس:
-
(1)
حيث تكون ak عدديات، تسمى إحداثيات (أو مكونات) المتجه v فيما يتعلق بالأساس B, و bik (k = 1, ..., n) عناصر B.الاستقلال الخطي يعني أن تكون الإحداثيات ak بشكل فريد لأي متجه في الفضاء المتجه.
على سبيل المثال، متجهات الإحداثيات e1 = (1, 0, ..., 0), e2 = (0, 1, 0, ..., 0), إلى en = (0, 0, ..., 0, 1)، تشكل أساساً لـ Fn، تسمى الأساس القياسي، عند أي متجه (x1, x2, ..., xn) يمكن التعبير عنها بشكل فريد كمجموعة خطية من هذه المتجهات:
- (x1, x2, ..., xn) = x1(1, 0, ..., 0) + x2(0, 1, 0, ..., 0) + ... + xn(0, ..., 0, 1) = x1e1 + x2e2 + ... + xnen.
الإحداثيات المقابلة x1, x2, ..., xn هي فقط الإحداثيات الديكارتية للمتجه.
كل فضاء متجه له أساس. هذا يتبع من ليما زورن، الصيغة المكافئة لـ بديهية الاختيار.[20]بالنظر إلى البديهيات الأخرى في نظرية مجموعة زرميلو-فرنكل، فإن وجود القواعد يعادل بديهية الاختيار.[21] تشير ليما للترشيح الفائق، وهي أضعف من بديهية الاختيار، إلى أن جميع قواعد فضاء متجه معين لها نفس عدد العناصر، أو عنصر أساسي (راجع. نظرية الأبعاد لفضاءات المتجهات).[22]يطلق عليه البعد لفضاء المتجه، ويُشار إليه بـ V الخافتة. إذا كان الفضاء موزعاً على العديد من المتجهات بشكل محدود، فيمكن إثبات العبارات المذكورة أعلاه بدون مثل هذه المدخلات الأساسية من نظرية المجموعة.[23]
أبعاد فضاء الإحداثيات Fn هي n، حسب الأساس الموضح أعلاه. تم تقديم أبعاد الحلقة متعددة الحدود F[x] أعلاهقالب:Huh على أنها لا حصر لها، فالأساس مُعطى بواسطة 1, x, x2, ... من باب أولي، أبعاد فضاءات الدوال الأكثر عمومية، مثل فضاء الدوال على بعض الفترات (المحددة أو غير المحدودة)، هي لانهائية.[nb 4]في ظل افتراضات الانتظام المناسبة بشأن المعاملات المتضمنة، فإن بُعد فضاء الحل في معادلة تفاضلية عادية تساوي درجة المعادلة.[24] على سبيل المثال، فضاء الحل لـ المعادلة أعلاهقالب:Huhتم إنشاؤه بواسطة e−x and xe−x. هاتان الدالتان مستقلتان خطياً على R، لذا فإن بُعد هذا الفضاء هو اثنان، كما هي درجة المعادلة.
يمكن اعتبار منشور الحقل على النسبية Q كفضاء متجه على Q (من خلال تعريف إضافة المتجه كإضافة مجال، تعريف الضرب العددي على أنه مضاعفة المجال بواسطة عناصر Q، وبخلاف ذلك تجاهل مضاعفة المجال). البعد (أو الدرجة) لنشر المجال Q(α) على Q يعتمد على α. إذا حققت α بعض المعادلات متعددة الحدود
المخططات والمصفوفات الخطية
يمكن التعبير عن العلاقة بين الفضائين المتجهين بواسطة مخطط خطي أو تحويل خطي. إنها دوال تعكس بنية الفضاء المتجه، أي أنها تحافظ على المجاميع والضرب العددي:
- و f(a · v) a · f(v) لكل v و w في V, كل a في F.[27]
يكون التماثل الشكلي مخططاً خطياً f : V → W بحيث يوجد مخطط عكسي g : W → V، وهو مخطط مثل التراكيب f ∘ g : W → W و g ∘ f : V → V هي مخططات المطابقة. بالتساوي، f هي في نفس الوقت (إدخالية) واحد لواحد وقائمة على (التنبؤية).[28] إذا كان هناك تماثل بين V و W، فإن الفضائين يقال أنهما متماثلين؛ هم بعد ذلك متطابقون بشكل أساسي كفضاءات متجهة، حيث يتم نقل جميع المطابقات الموجودة في V، عبر f، إلى مماثلة في W والعكس بالعكس عبر g.
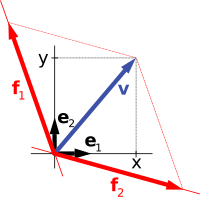
على سبيل المثال، الفضاءات المتجهة "الأسهم في المستوى" و "الأزواج المرتبة من الأرقام" في المقدمة متشابهة الشكل: سهم مستوٍ v يتجه في الأصل بعض (ثوابت) النظام الإحداثي يمكن التعبير عنه كزوج مرتبي من خلال النظر في x- و مكون-y للسهم، كما هو موضح في الصورة على اليمين. على العكس من ذلك، بالنظر إلى الزوج(x, y)، السهم يمر بـ x إلى اليمين (أو إلى اليسار، إذا كانت x سلبي)، و y لأعلى (لأسفل، إذا كانت y سالبة) تعود السهم v.
تشكل المخططات الخطية V → W بين فضائين متجهتين فضاء متجهي HomF(V, W)، يُشار إليها أيضاً بـ L(V, W).[29] يسمى فضاء المخططات الخطية من V إلى F الفضاء المتجهي الثنائي، ويشار إليها V∗.[30] عبر مخطط الإدخال الطبيعي V → V∗∗، يمكن تضمين أي فضاء متجه في ثنائية؛ يكون المخطط متشابهاً إذا وفقط إذا كان الفضاء محدود الأبعاد.[31]
بمجرد اختيار أساس V، يتم تحديد المخططات الخطية f : V → W تماماً من خلال تحديد الصور من المتجهات الأساسية، لأن أي عنصر من عناصر V يتم التعبير عنه بشكل فريد كمجموعة خطية منها.[32] إذا كان dim V = dim W، توافق 1 إلى 1 بين قواعد ثابتة لـ V و W يؤديان إلى ظهور مخطط خطي يحدد أي عنصر أساسي لـ V إلى عنصر الأساس المقابل لـ W. فهو تماثل، من خلال تعريفه ذاته.[33] لذلك، يكون الفضاءان المتجهان متشابهين إذا كانت أبعادهما متوافقة والعكس صحيح. هناك طريقة أخرى للتعبير عن ذلك وهي أن أي فضاء متجه مصنف تماماً (إلى أن يتماثل الشكل) من خلال بعده، وهو رقم واحد. على وجه الخصوص، أي n-بُعد F-فضاء متجه V متماثل بالنسبة إلى Fn. ومع ذلك، لا يوجد تماثل متعارف عليه أو مفضل؛ في الحقيقة تماثل الشكل φ : Fn → V يعادل اختيار أساس V، عن طريق تعيين الأساس القياسي لـ Fn إلى V، عبر φ. حرية اختيار الأساس المناسب مفيدة بشكل خاص في سياق الأبعاد اللانهائية ؛ انظر أدناه.قالب:Huh
المصفوفات
المصفوفات هي فكرة مفيدة لترميز المخططات الخطية.[34] وهي مكتوبة على هيئة مصفوفة مستطيلة من العدديات كما في الصورة على اليمين. أي m-ب-n المصفوفة A تؤدي إلى ظهور مخطط خطي من Fn to Fm، من خلال ما يلي
- , حيث تشير إلى الجمع،
أو، باستخدام ضرب المصفوفة للمصفوفة A مع متجه الإحداثيات x:
- x ↦ Ax.
علاوة على ذلك، بعد اختيار قواعد V و W، أي مخطط خطي f : V → W بشكل فريد بواسطة مصفوفة عبر هذه المهمة.[35]
المحدد det (A) من مصفوفة مربعة A هو مقياس يخبرك ما إذا كان المخطط المرتبط متماثل أم لا: لكي يكون الأمر كذلك، يكفي وضروري أن يكون المحدد غير صفري.[36]التحويل الخطي لمصفوفة Rn المقابل لمصفوفة حقيقية n-by-n هو الحفاظ على الاتجاه إذا وفقط إذا كان محدده موجباً.
القيم الذاتية والمتجهات الذاتية
التشابه الشكلي، المخططات الخطية f : V → V، لها أهمية خاصة لأنه في هذه الحالة المتجهات v يمكن مقارنتها بصورتها ضمن f, f(v). أي متجه غير صفريv يحقق λv = f(v)، حيث أن λ عددية، يسمى المتجه الذاتي لـ of f مع القيمة الذاتية λ.[nb 5][37]بالتساوي، v هو عنصر من النواة للاختلاف f − λ · Id (حيث المعرف هو مخطط المطابقة V → V). إذا كانت V ذات بُعد محدود، فيمكن إعادة صياغة هذا باستخدام المحددات: f ذات قيمة ذاتية λ مكافئة إلى
- det(f − λ · Id) = 0.
بتهجئة تعريف المحدد، يمكن اعتبار التعبير الموجود على الجانب الأيسر دالة كثيرة الحدود في λ، تسمى مميزة كثير الحدود لـ f.[38] إذا كان المجال F كبيراً بما يكفي لاحتواء صفر من كثير الحدود هذا (والذي يحدث تلقائياً لـ F المغلق جبرياً، مثل F = C) أي مخطط خطي له متجه واحد على الأقل. قد يمتلك أو لا يمتلك فضاء المتجه V الأساس الذاتي، وهو أساس يتكون من متجهات ذاتية. هذه الظاهرة تحكمها صيغة جوردان القانونية للمخطط.[39][nb 6]تشكل مجموعة جميع المتجهات الذاتية المقابلة لقيمة ذاتية معينة لـ f فضاء متجه يُعرف باسم الفضاء الذاتي المقابل للقيمة الذاتية (و f) في السؤال. لتحقيق النظرية الطيفية، التعبير المقابل في الحالة اللانهائية الأبعاد، هناك حاجة إلى آلية التحليل الدالي، see أدناه.قالب:Huh
البناء الأساسي
بالإضافة إلى الأمثلة الملموسة أعلاه، هناك عدد من البنى الجبرية الخطية المعيارية التي تنتج فضاءات متجهة مرتبطة بأخرى معينة. بالإضافة إلى التعريفات الواردة أدناه، فهي تتميز أيضًا بـ الخصائص الشاملة، والتي تحدد أداة X عن طريق تحديد المخططات الخطية من {X إلى أي فضاء متجهي آخر.
الفضاءات الفرعية وفضاءات حاصل القسمة
تسمى المجموعة الفرعية الغير فارغة W لفضاء متجه V بالمغلقة تحت عملية الجمع والضرب العددي (وبالتالي تحتوي على0- متجه V) يُطلق عليه الفضاء الجزئي الخطي لـV، أو ببساطة الفضاء الجزئي لـ V، عندما يكون الفضاء المحيط بشكل لا لبس فيه عبارة عن فضاء متجه.[40][nb 7]الفضاءات الفرعية لـV هي فضاءات متجهة (فوق نفس المجال) في حد ذاتها. يُطلق على تقاطع جميع الفضاءات الفرعية التي تحتوي على مجموعة معينة من المتجهات S من المتجهات بامتدادها، وهي أصغر فضاء فرعيلـV يحتوي على المجموعة S. معبراً عنه من حيث العناصر، فإن الامتداد هو الفضاء الفرعي الذي يتكون من جميع التركيبات الخطية لعناصر S.[41]
الفضاء الفرعي الخطي للبعد 1 هو خط متجه. الفضاء الفرعي الخطي للبعد 2 هو مستوى متجه. الفضاء الفرعي الخطي الذي يحتوي على جميع العناصر باستثناء أحد أسس الفضاء المحيط هو المستوى الفائق المتجه. في فضاء متجه ذي بُعد محدود n، فإن المستوي المتجهي الفائق بالتالي فضاء فرعي للبعد n – 1.
يكون النظير إلى الفضاءات الجزئية هو فضاء متجه حاصل القسمة.[42] بالنظر إلى أي فضاء فرعي W ⊂ V، يتم تعريف فضاء حاصل القسمة V/W ("V المعياري W") كالتالي: كمجموعة، مكونة من v + W = {v + w : w ∈ W}, حيث يكون v متجهاً عشوائياً في V.مجموع هذين العنصرين v1 + W و v2 + W يكون (v1 + v2) + W, و يعطى الضرب العددي بواسطة a · (v + W) = (a · v) + W. النقطة الأساسية في هذا التعريف أن v1 + W = v2 + W إذا وفقط إذا وقع الاختلاف بين v1 و v2 lies في W.[nb 8] وبهذه الطريقة، فإن فضاء حاصل القسمة "تنسى" المعلومات الموجودة في الفضاء الفرعي W.
تتكون نواة ker(f) للمخطط الخطي f : V → W من متجهات v التي تم تعيينها إلى 0 في W.[43] تكون النواة و صورة im(f) = {f(v) : v ∈ V} هي فضءات فرعية لـV و W، على التوالي.[44]يعد وجود النوى والصور جزءاً من العبارة القائلة بأن تصنيف فضاءات المتجهات (على مجال ثابت F) هي تصنيف تآلفي، أي مجموعة من الكائنات الرياضية و المخططات التي تحافظ على البنية بينهما ( التصنيف) الذي يشبه إلى حد كبير تصنيف مجموعات تآلفية.[45]وبسبب هذا، فإن العديد من العبارات مثل نظرية التماثل الأولى (تسمى أيضاً نظرية الرتبة - العدم في المصطلحات المتعلقة بالمصفوفة)
- V / ker(f) ≡ im(f).
ويمكن صياغة وإثبات نظرية تماثل الشكل الثانية والثالثة بطريقة تشبه إلى حد بعيد العبارات المقابلة لـ المجموعات.
أحد الأمثلة المهمة هو نواة المخطط الخطي x ↦ Ax لبعض المصفوفات الثابتة A، مثل أعلاه.قالب:Huh تكون نواة هذه الخريطة هي الفضاء الفرعي للمتجهات x مثل أن Ax = 0، وهي بالضبط مجموعة الحلول لـ نظام المعادلات الخطية المتجانسة التي تنتمي إلى A. يمتد هذا المفهوم أيضًا إلى المعادلات التفاضلية الخطية
- ، حيث المعاملات ai هي دوال في x أيضاً.
في المخطط المقابل
- ,
تظهر مشتقات الدالة f خطياً (على سبيل المثال، f′′(x)2). نظراً لأن التفاضل إجراء خطي (أي (f + g)′ = f′ + g ′ و (c·f)′ = c·f′ لثابت c) هذا التخصيص خطي، ويسمى عامل التفاضل الخطي. على وجه الخصوص، تشكل حلول المعادلة التفاضلية D(f) = 0 فضاءً متجهياً (على R أو C)..
الجداء المباشر والمجموع المباشر
يعد الجداء المباشر لفضاءات المتجه و المجموع المباشر لفضاءات المتجهات طريقتين لدمج عائلة مفهرسة من فضاءات المتجهات في فضاء متجهي جديد.
الجداء المباشر لعائلة من الفضاءات المتجه Vi المكون من مجموعة من جميع مجموعات العناصر (vi)i ∈ I،التي تحدد لكل مؤشر i في بعض مجموعة الفهرس I عنصر vi من Vi.[46] يتم تنفيذ عمليات الجمع والضرب العددي بشكل مكون. أحد أشكال هذا البناء هو المجموع المباشر (يُسمى أيضاً الجداء المشترك ويشار إليه بـ )، حيث يُسمح فقط بمجموعات العناصر التي تحتوي على متجهات غير صفرية كثيرة. إذا كانت مجموعة الفهرس I محدودة، يتفق البناءان، لكنهما مختلفان بشكل عام.
جداء الموتر
جداء الموتر V ⊗F W، أو ببساطة V ⊗ W، لفضائين متجهتين V و W هي واحدة من المفاهيم المركزية لـ الجبر متعدد الخطية التي تتعامل مع توسيع المفاهيم مثل المخططات الخطية إلى عدة متغيرات. يسمى المخطط g : V × W → X ثنائي الخطية إذا كانت g خطية في كلا المتغيرين v و w. وهذا يعني، بالنسبة للمخطط الثابت w يكون v ↦ g(v, w) خطي بالمعنى الوارد أعلاه وبالمثل بالنسبة لـ v الثابتة.
جداء الموتر هو فضاء متجهي معين، وهي مستقبل شامل للمخططات ثنائية الخطية g، على النحو التالي. يتم تعريفه على أنه فضاء متجه يتكون من مجموعات محدودة (اصطلاحية) من الرموز تسمى الموترات
- v1 ⊗ w1 + v2 ⊗ w2 + ... + vn ⊗ wn,
تخضع للقواعد
- a · (v ⊗ w) = (a · v) ⊗ w = v ⊗ (a · w), حيث تكون a عددية،
- (v1 + v2) ⊗ w = v1 ⊗ w + v2 ⊗ w, و
- v ⊗ (w1 + w2) = v ⊗ w1 + v ⊗ w2.[47]

تضمن هذه القواعد أن المخطط f من V × W إلى V ⊗ W التي تعين مجموعة عناصر (v, w) إلى v ⊗ w ثنائية الخطية. تنص الحالة الشاملة على أن أي فضاء متجهي X و أي مخطط ثنائي الخطية g : V × W → X، يوجد مخطط فريد u، موضح في الرسم التخطيطي بسهم منقط، التكوين مع f يساوي g: u(v ⊗ w) = g(v, w).[48] وهذا ما يسمى الخاصية الشاملة لجداء الموتر، وهو مثال للطريقة - المستخدمة كثيراً في الجبر المجرد المتقدم - لتعريف الأدوات بشكل غير مباشر عن طريق تحديد مخططات من أو إلى هذه الأداة.
الفضاءات المتجهية مع بنية إضافية
من وجهة نظر الجبر الخطي، تُفهم الفضاءات المتجهية تماماً بقدر ما تتميز أي فضاء متجه، حتى تماثل الشكل، بأبعاده. ومع ذلك، لا تقدم فضاءات المتجهات في حد ذاتها إطاراً للتعامل مع السؤال - المهم في التحليل - ما إذا كانت سلسلة من تقارب الدوال مع دالة أخرى. وبالمثل، لا يتم تكييف الجبر الخطي للتعامل مع متسلسلة لانهائية، لأن عملية الإضافة تسمح فقط بإضافة عدد محدود من المصطلحات. لذلك، تتطلب احتياجات التحليل الدالي النظر في بنى إضافية.
يمكن إعطاء فضاء متجه ترتيب جزئي ≤، يمكن بموجبه مقارنة بعض المتجهات.[49] على سبيل المثال ، n - فضاء حقيقي ذو أبعاد Rn يمكن ترتيبها بمقارنة متجهاتها بشكل مكون. يعتبر ترتيب الفضاء المتجه، على سبيل المثال فضاء ريز، أساسياً لـ تكامل لبگ، والذي يعتمد على القدرة على التعبير عن دالة كفرق بين دالتين إيجابيتين
- f = f+ − f−,
حيث تشير f+ إلى الجزء الموجب من f و f− الجزء السلبي.[50]
الفضاءات المتجهة المعيارية وفضاءات الجداء الداخلي
يتم إجراء "قياس" المتجهات عن طريق تحديد معيار، معطى يقيس أطوال المتجهات، أو بواسطة جداء داخلي، والذي يقيس الزوايا بين المتجهات. يتم الإشارة إلى المعايير والجداءات الداخلية d و ، على التوالي. يستلزم معطى الجداء الداخلي أنه يمكن تحديد أطوال المتجهات أيضاً، من خلال تحديد المعيار المرتبط . تُعرف فضاءات المتجهات الممنوحة بمثل هذه البيانات باسم فضاءات المتجهات المعيارية و فضاءات الجداء الداخلي، على التوالي.[51]
يمكن تجهيز الفضاء الإحداثي Fn بالجداء النقطي القياسي:
في R2، وهذا ما يعكس المفهوم المشترك للزاوية بين متجهين x و y، بواسطة قانون جيب التمام:
وبسبب هذا، تسمى اثنين من المتجهات المحققة بالمتعامدة. يتم استخدام نوع مهم من الجداء النقطي القياسي في فضاء منكوڤسكي: R4 الممنوح بجداء لورنتز
على عكس الحداء النقطي القياسي، فهو ليس تعريف إيجابي: ولكنه يأخذ أيضاً قيماً سالبة، على سبيل المثال . إن تحديد الإحداثي- المطابق للزمن الرابع، بدلاً من الأبعاد المكانية الثلاثة - مما يجعله مفيداً في المعالجة الرياضية لـ النسبية الخاصة.
فضاءات المتجهات الطوبولوجية
يتم التعامل مع أسئلة التقارب من خلال النظر في فضاءات المتجه V التي تحمل طوبولوجيا ملائمة، وهي بنية تسمح للمرء بالتحدث عن العناصر التي تكون قريبة من بعضها البعض.[53][54] يعني التوافق هنا أن الجمع والضرب العددي يجب أن يكون مخططاً مستمراً. تقريباً، إذا اختلفت 'x و y في V, و a في F بمقدار محدد، فإن x + y و ax.[nb 9] لفهم تحديد المقدار الذي يتغير فيه العدد، يجب أن يحمل المجال F أيضاً طوبولوجيا في هذا السياق؛ الاختيار الشائع هو الأعداد الحقيقيو أو العقدية. في مثل هذه الفضاءات المتجهية الطوبولوجية يمكن للمرء أن يأخذ في الاعتبار متسلسلة من المتجهات. يشير المجموع اللانهائي: إلى نهاية المجاميع الجزئية المنتهية المقابلة من التسلسل (fi)i∈N لعناصر V. على سبيل المثال، يمكن أن تكون fi تواابع (حقيقية أو عقدية) تنتمي إلى بعض فضاء الدالة V، وفي هذه الحالة تكون المتسلسلة متسلسلة دالية. يعتمد وضع التقارب للمتسلسلة على الهيكل المفروض على فضاء الدالة. في مثل هذه الحالات، يعد التقارب النقطي و التقارب المنتظم مثالين شهيرين.
تتمثل إحدى طرق ضمان وجود نهايات لمتسلسلة لانهائية معينة في حصر الانتباه على الفضاءات حيث يكون لأي متسلسلة كوشي نهاية؛ يسمى هذا الفضاء المتجه كاملاً. تقريباً، يكون فضاء المتجه كاملاً بشرط أن يحتوي على جميع النهايات اللازمة. على سبيل المثال، يكون فضاء المتجه للعديد من الحدود على فاصل الوحدة [0،1]، المزود بـ طوبولوجيا التقارب المنتظم غير مكتملاً لأن أي دالة مستمرة على [0،1] يمكن تقريبها بشكل موحد من خلال تسلسل كثيرات الحدود، من خلال نظرية تقريب ويرشتراس.[55]في المقابل، يكتمل فضاء جميع الدوال المستمرة على [0،1] بنفس الهيكل.[56] تؤدي القاعدة إلى ظهور طوبولوجيا من خلال تحديد أن متسلسلة من المتجهاتvn تتقارب إلى v إذا وفقط إذا
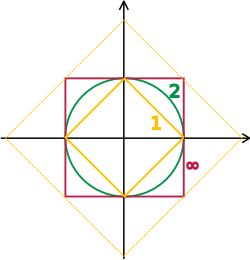
تكون فضاءات باناخ و هلبرت عبارة عن فضاءات متجهية طوبولوجية كاملة تُعطى طبولوجيا، على التوالي، بواسطة معيار وجداء داخلي. تركز دراستهم - وهي جزء أساسي من التحليل الدالي - على الفضاءات المتجهية اللانهائية الأبعاد، نظرًا لأن جميع المعايير على الفضاءات المتجهية الطوبولوجية ذات الأبعاد المحدودة تؤدي إلى نفس مفهوم التقارب.[57] تُظهر الصورة الموجودة على اليمين تكافؤ معيار-1 و معيار-∞ على R2: نظراً لأن كرات الوحدة تحيط ببعضها البعض، يتقارب التسلسل إلى الصفر في معيار واحد فقط إذا كان كذلك في المعيار الآخر. ومع ذلك، في حالة الأبعاد اللانهائية، سيكون هناك عموماً طبولوجيا غير متكافئة، مما يجعل دراسة الفضاءات المتجهية الطوبولوجية أكثر ثراءً من دراسة الفضاءات المتجهية بدون بيانات إضافية.
من وجهة نظر مفاهيمية، يجب أن تتطابق جميع المفاهيم المتعلقة بفضاءات المتجهات الطوبولوجية مع الطوبولوجيا. على سبيل المثال، بدلاً من النظر في جميع المخططات الخطية (تسمى أيضاً V → W الدالية)، فإن المخططات بين فضاءات المتجهات الطوبولوجية مطلوبة من أجل تكون مستمرة.[58]على وجه الخصوص، يتكون (الفضاء المزدوج (الطبولوجي)V∗ من دوال مستمرة V → R (أو إلى C). تهتم نظرية هان – باناخ الأساسية بفصل الفضاءات الفرعية لفضاءات المتجهات الطوبولوجية المناسبة بدوال مستمرة.[59]
فضاءات باناخ
فضاءات باناخ، التي قدمها ستيفان باناخ، هي فضاءات متجهية معيارية كاملة.[60]
يتكون المثال الأول فضاء المتجه من متجهات لا حصر لها مع مداخل حقيقية الذي يعطى -norm بواسطة
- من أجل and .
تكون الطبولوجيا على الفضاء اللامتناهي الأبعاد متكافئة مع اختلاف . على سبيل المثال، تسلسل المتجهات , حيث تكون مكونات الأولى والمكونات التالية ، متقاربة مع المتجه الصفري من أجل , ولكن ليس لأجل :
- , لكن
بشكل عام أكثر من تسلسلات الأرقام الحقيقية، تكون الدوال مزودة بمعيار يحل محل المجموع أعلاه بواسطة تكامل ليبزگ
يسمى فضاء دالة قابلة للتكامل على المجال (على سبيل المثال فاصل زمني) محققاً , ومزودة بهذا المعيار بفضاءات ليبزگ، يشار إليها .[nb 10]
تكون هذه الفضاءات مكتملة.[61] (إذا استخدم المرء تكامل ريمن بدلاً من ذلك، فإن الفضاء "ليس" كاملاً، والذي قد يُنظر إليه على أنه مبرر لنظرية تكامل ليبزگ.[nb 11]) وهذا يعني بشكل ملموس أنه بالنسبة لأي تسلسل من دوال ليبزگ القابلة للتكامل with , تحقق الشرط
توجد دالة تنتمي إلى فضاء المتجه مثل
يؤدي فرض شروط التقييد ليس فقط على الدالة، ولكن أيضاً على مشتقاتها إلى فضاء سوبوليڤ.[62]
فضاءات هلبرت
تُعرف فضاءات الجداء الداخلي الكاملة باسم فضاءات هلبرت، تكريماً لـ ديڤد هلبرت.[63] يعطى فضاء هلبرت L2(Ω)، مع الجداء الداخلي بواسطة
حيث تشير إلى المرافق العقدي لـ g(x),[64][nb 12] وهي حالة أساسية.
بحكم التعريف، في فضاء هلبرت، تتقارب أي من متسلسلة كوشي إلى نهاية. على العكس من ذلك، فإن العثور على تسلسل من الدوال fn ذات الخصائص المرغوبة التي تقترب من دالة حد معينة، أمر بالغ الأهمية أيضاً. أنشأ التحليل الأولي، تحت ستار تقريب تايلر، تقديراً تقريبياً لـ الدوال لبقابلة للتفاضل و f بواسطة كثيرات الحدود.[65]من خلال نظرية ستون-ويرشتراس، يمكن تقريب كل دالة مستمرة في [a, b] كما هو مطلوب بواسطة كثير الحدود.[66]يُطلق على تقنية تقريب مماثلة بواسطة الدالة المثلثية بشكل شائع منشور فورييه، ويتم تطبيقها كثيراً في الهندسة، راجع أدناه.قالب:Huh بشكل أكثر عمومية، ومن الناحية المفاهيمية أكثر، تنتج النظرية وصفاً بسيطاً لماهية الدوال الأساسية، أو، في فضاءات هلبرت المجردة، ما هي المتجهات الأساسية الكافية لتوليد فضاء هلبرت H، بمعنى أن غالق امتدادها (أي، مجموعات خطية محدودة وحدود تلك) هي الفضاء الكامل. تسمى هذه المجموعة من الوظائف بـ أساس لـ H، وتُعرف أصلها باسم بُعد فضاء هلبرت.[nb 13]لا تعرض النظرية دوال الأساس المناسبة فقط باعتبارها كافية لأغراض التقريب، ولكن أيضاً مع عملية گرام-شميت، فهي تمكن المرء من بناء أساس المتجهات المتعامدة.[67]هذه القواعد المتعامدة هي تعميم فضاء هلبرت لمحاور الإحداثيات في الأبعاد المحدودة للفضاء الإقليدي.
يمكن تفسير حلول المعادلات التفاضلية المختلفة من حيث فضاءات هلبرت. على سبيل المثال، يؤدي عدد كبير جداً من المجالات في الفيزياء والهندسة إلى مثل هذه المعادلات وغالباً ما يتم استخدام الحلول ذات الخصائص الفيزيائية المعينة كدوال أساسية، وغالباً ما تكون متعامدة.[68]كمثال من الفيزياء، تصف معادلة شرودنگر المعتمدة على الزمن في ميكانيكا الكم تغير الخصائص الفيزيائية في الزمن عن طريق معادلة تفاضلية جزئية، والتي تسمى حلولها الدوال الموجية.[69] تتوافق القيم المحددة للخصائص الفيزيائية مثل الطاقة أو القوة الدافعة مع القيم الذاتية المعينة لعامل تفاضلي (خطي) وتسمى دوال الموجة المرتبطة بالحالات الذاتية. تحلل النظرية الطيفية عامل دمج خطي يعمل على دوال من حيث هذه الدوال الذاتية وقيمها الذاتية.[70]
الجبر على المجالات

لا تمتلك الفضاءات المتجهة العامة عملية ضرب بين المتجهات. فضاء المتجه المجهز بـ عامل ثنائي الخطية المحدد لمضاعفة متجهين هو الجبر على المجال.[71] تنبع العديد من الجبر من الدوال على أداة هندسية: بما أن الدوال ذات القيم في مجال معين يمكن أن تتضاعف نقطياً، فإن هذه الكيانات تشكل الجبر. على سبيل المثال، تعتمد نظرية ستون-ويرشتراس على جبر باناخ والذي يمثل فضاءات وجبر باناخ.
يستفيد الجبر التبديلي بشكل كبير من حلقات كثيرة الحدود في متغير واحد أو عدة متغيرات، مقدمةabove.قالب:Huh يكون ضربهم تبديلياً و ترابطياً. تشكل هذه الحلقات و حاصل القسمة أساس الهندسة الجبرية لأنها حلقات الدوال الهندسية الجبرية.[72]
مثال آخر مهم هو جبر لي، وهو ليست تبادلياً ولا ترابطياً، لكن الخطأ في أن يكون ذلك محدوداً بالقيود ([x, y] يشير جداء x و y):
- [x, y] = −[y, x] (اللاتبديلية)، و
- [x, [y, z]] + [y, [z, x]] + [z, [x, y]] = 0 (لمطابقة جاكوبي).[73]
تتضمن الأمثلة فضاء متجه لمصفوفات n-by-n، مع [x, y] = xy − yx، المبدل لمصفوفتين، و R3، تم منحهما الجداء المتقاطع.
الجبر الموتر T(V) هي طريقة اصطلاحية لإضافة الجداءات إلى أي فضاء متجه V للحصول على الجبر.[74] كفضاء متجهي، فهو يمتد برموز تسمى موترات بسيطة
- v1 ⊗ v2 ⊗ ⋯ ⊗ vn، حيث تختلف درجة n.
يُعطى الضرب من خلال تسلسل هذه الرموز، وفرض القانون التوزيعي تحت الإضافة، وطلب بأن يتنقل الضرب العددي مع جداء الموتر ⊗، تماماً كما هو الحال مع جداء الموتر لفضائين متجهتين أعلاه.قالب:Huh بشكل عام، لا توجد علاقات بين v1 ⊗ v2 و v2 ⊗ v1. يؤدي إجبار هذين العنصرين على التساوي إلى الجبر المتماثل، في حين يعود تأثير v1 ⊗ v2 = − v2 ⊗ v1 the إلى الجبر الخارجي.[75]
عندما يتم ذكر مجال F صراحةً، فإن المصطلح الشائع المستخدم هو جبر-F.
التطبيقات
تحتوي فضاءات المتجهات على العديد من التطبيقات لأنها تحدث بشكل متكرر في ظروف مشتركة، أي في أي مكان تشارك فيه دوال ذات قيم في بعض المجالات. فهي توفر إطاراً للتعامل مع المشكلات التحليلية والهندسية، أو تُستخدم في تحويل فورييه. هذه القائمة ليست شاملة: يوجد العديد من التطبيقات الأخرى، على سبيل المثال في التحسين. يمكن صياغة مبرهنة تصغير الأعظم لـ نظرية الألعاب التي تنص على وجود نتيجة فريدة عندما يلعب جميع اللاعبين على النحو الأمثل وإثباتها باستخدام أساليب فضاءات المتجهات.[76]تنقل نظرية التمثيل بشكل مثمر الفهم الجيد للجبر الخطي والفضاءات المتجهة إلى المجالات الرياضية الأخرى مثل نظرية المجموعات.[77]
Distributions
A distribution (or generalized function) is a linear map assigning a number to each "test" function, typically a smooth function with compact support, in a continuous way: in the aboveقالب:Huh terminology the space of distributions is the (continuous) dual of the test function space.[78] The latter space is endowed with a topology that takes into account not only f itself, but also all its higher derivatives. A standard example is the result of integrating a test function f over some domain Ω:
When Ω = {p}, the set consisting of a single point, this reduces to the Dirac distribution, denoted by δ, which associates to a test function f its value at the p: δ(f) = f(p). Distributions are a powerful instrument to solve differential equations. Since all standard analytic notions such as derivatives are linear, they extend naturally to the space of distributions. Therefore, the equation in question can be transferred to a distribution space, which is bigger than the underlying function space, so that more flexible methods are available for solving the equation. For example, Green's functions and fundamental solutions are usually distributions rather than proper functions, and can then be used to find solutions of the equation with prescribed boundary conditions. The found solution can then in some cases be proven to be actually a true function, and a solution to the original equation (for example, using the Lax–Milgram theorem, a consequence of the Riesz representation theorem).[79]
تحليل فورييه
يشكل حل الدالة الدورية في مجموع الدوال المثلثية متسلسلة فورييه، وهي تقنية مستخدمة كثيراً في الفيزياء والهندسة.[nb 14][80] عادةً ما يكون فضاء المتجه الأساسي هو فضاء هلبرتL2(0, 2π)، والتي لها دالات mx و cos mx (m عدد صحيح) والذي يشكل أساساً متعامداً.[81]يكون منشور فورييه للدالة f L2 هو
يُطلق على المعاملات am و bm بمعاملات فورييه من f ويتم حسابها بواسطة الصيغ[82]
- ,
من الناحية الفيزيائية، يتم تمثيل الدالة على أنها تراكب من أمواج جيبية وتعطي المعاملات معلومات حول الطيف الترددي الخاص بالدالة.[83] يشيع أيضاً استخدام شكل رقم عقدي من متسلسلة فورييه.[82] الصيغ الملموسة أعلاه هي نتائج ثنائية رياضية أكثر عمومية تسمى ثنائية پونترياجن.[84]بالتطبيق على المجموعة R، ينتج تحويل فورييه الكلاسيكي؛ أحد التطبيقات في الفيزياء هو شبكة تبادلية، حيث تكون المجموعة الأساسية عبارة عن فضاء متجه حقيقي ذي أبعاد محدودة ومزود بمعطى إضافي لـ شبكة مواقع ترميز الذرات في البلورات.[85]
تُستخدم متسلسلات فورييه لحل مشاكل القيمة الحدية في المعادلات التفاضلية الجزئية.[86]في عام 1822، استخدم فورييه هذه التقنية لأول مرة لحل معادلة الحرارة.[87] يمكن استخدام نسخة منفصلة من سلسلة فورييه في تطبيقات أخذ العينات حيث تُعرف قيمة الدالة فقط عند عدد محدود من النقاط المتباعدة بشكل متساوٍ. في هذه الحالة، تكون سلسلة فورييه محدودة وقيمتها تساوي قيم العينة في جميع النقاط.[88] تُعرف مجموعة المعاملات باسم تحويل فورييه المتقطع (DFT) لتتابع العينة المحدد. DFT هو أحد الأدوات الرئيسية لـ معالجة الإشارات الرقمية، وهو مجال تشمل تطبيقاته الرادار، ترميز الكلام، ضغط الصور.[89] تنسيق الصورة JPEG هو تطبيق لـ تحويل جيب التمام المتقطع.[90]
تحويل فورييه السريع عبارة عن خوارزمية لحساب تحويل فورييه المتقطع بسرعة.[91]لا يستخدم فقط لحساب معاملات فورييه ولكن أيضاً باستخدام نظرية الالتفاف لحساب الالتفاف لمتتابعين محددين.[92] يتم تطبيقها بدورها في المرشحات الرقمية[93]وكخوارزمية الضرب السريعة للعديد من الحدود والأعداد الصحيحة الكبيرة (خوارزمية شونهگ-شتڠاسن).[94][95]
الهندسة التفاضلية

المستوي المماسي على سطح عند نقطة ما هو بطبيعة الحال فضاء متجه يتم تحديد أصله بنقطة الاتصال. المستوى المماس هو أفضل تقريب خطي، أو خطية، لسطح عند نقطة.[nb 15]حتى في الفضاء الإقليدي ثلاثي الأبعاد، لا توجد عادة طريقة طبيعية لوصف أساس المستوى المماسي، وبالتالي يُنظر إليه على أنه فضاء متجهي مجرد بدلاً من فضاء إحداثي حقيقي. الفضاء المماسي هو التعميم لأبعاد أعلى طية تفاضلية.[96]
تكون الطيات الريمانية عبارة عن طيات ذات فضاءات مماسية مُنحت مع جداء داخلي مناسب.[97]يرمز المشتق من ذلك، موتر انحناء ريمن كل الانحناءات لطية في أداة واحدة، والذي يجد تطبيقات في النسبية العامة، على سبيل المثال، حيث يصف موتر انحناء أينشتاين محتوى المادة والطاقة في الزمكان.[98][99]يمكن إعطاء الفضاء المماسي لمجموعة لي بشكل طبيعي بنية جبر لي ويمكن استخدامها لتصنيف مجموعة لي المدمجة.[100]
Generalizations
Vector bundles
A vector bundle is a family of vector spaces parametrized continuously by a topological space X.[96] More precisely, a vector bundle over X is a topological space E equipped with a continuous map
- π : E → X
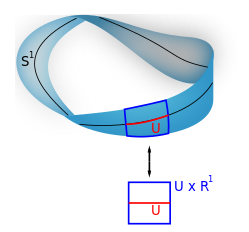
such that for every x in X, the fiber π−1(x) is a vector space. The case dim V = 1 is called a line bundle. For any vector space V, the projection X × V → X makes the product X × V into a "trivial" vector bundle. Vector bundles over X are required to be locally a product of X and some (fixed) vector space V: for every x in X, there is a neighborhood U of x such that the restriction of π to π−1(U) is isomorphic[nb 16] to the trivial bundle U × V → U. Despite their locally trivial character, vector bundles may (depending on the shape of the underlying space X) be "twisted" in the large (that is, the bundle need not be (globally isomorphic to) the trivial bundle X × V). For example, the Möbius strip can be seen as a line bundle over the circle S1 (by identifying open intervals with the real line). It is, however, different from the cylinder S1 × R, because the latter is orientable whereas the former is not.[101]
Properties of certain vector bundles provide information about the underlying topological space. For example, the tangent bundle consists of the collection of tangent spaces parametrized by the points of a differentiable manifold. The tangent bundle of the circle S1 is globally isomorphic to S1 × R, since there is a global nonzero vector field on S1.[nb 17] In contrast, by the hairy ball theorem, there is no (tangent) vector field on the 2-sphere S2 which is everywhere nonzero.[102] K-theory studies the isomorphism classes of all vector bundles over some topological space.[103] In addition to deepening topological and geometrical insight, it has purely algebraic consequences, such as the classification of finite-dimensional real division algebras: R, C, the quaternions H and the octonions O.
The cotangent bundle of a differentiable manifold consists, at every point of the manifold, of the dual of the tangent space, the cotangent space. Sections of that bundle are known as differential one-forms.
Modules
Modules are to rings what vector spaces are to fields: the same axioms, applied to a ring R instead of a field F, yield modules.[104] The theory of modules, compared to that of vector spaces, is complicated by the presence of ring elements that do not have multiplicative inverses. For example, modules need not have bases, as the Z-module (that is, abelian group) Z/2Z shows; those modules that do (including all vector spaces) are known as free modules. Nevertheless, a vector space can be compactly defined as a module over a ring which is a field, with the elements being called vectors. Some authors use the term vector space to mean modules over a division ring.[105] The algebro-geometric interpretation of commutative rings via their spectrum allows the development of concepts such as locally free modules, the algebraic counterpart to vector bundles.
Affine and projective spaces
Roughly, affine spaces are vector spaces whose origins are not specified.[106] More precisely, an affine space is a set with a free transitive vector space action. In particular, a vector space is an affine space over itself, by the map
- V × V → V, (v, a) ↦ a + v.
If W is a vector space, then an affine subspace is a subset of W obtained by translating a linear subspace V by a fixed vector x ∈ W; this space is denoted by x + V (it is a coset of V in W) and consists of all vectors of the form x + v for v ∈ V. An important example is the space of solutions of a system of inhomogeneous linear equations
- Ax = b
generalizing the homogeneous case b = 0 above.قالب:Huh[107] The space of solutions is the affine subspace x + V where x is a particular solution of the equation, and V is the space of solutions of the homogeneous equation (the nullspace of A).
The set of one-dimensional subspaces of a fixed finite-dimensional vector space V is known as projective space; it may be used to formalize the idea of parallel lines intersecting at infinity.[108] Grassmannians and flag manifolds generalize this by parametrizing linear subspaces of fixed dimension k and flags of subspaces, respectively.
See also
- Vector (mathematics and physics), for a list of various kinds of vectors
|
|
Notes
- ^ It is also common, especially in physics, to denote vectors with an arrow on top: v←.
- ^ This axiom and the next refer to two different operations: scalar multiplication: bv; and field multiplication: ab. They do not assert the associativity of either operation. More formally, scalar multiplication is a monoid action of the multiplicative monoid of the field F on the vector space V.
- ^ Some authors (such as Brown 1991) restrict attention to the fields R or C, but most of the theory is unchanged for an arbitrary field.
- ^ The indicator functions of intervals (of which there are infinitely many) are linearly independent, for example.
- ^ The nomenclature derives from German "eigen", which means own or proper.
- ^ See also Jordan–Chevalley decomposition.
- ^ This is typically the case when a vector space is also considered as an affine space. In this case, a linear subspace contains the zero vector, while an affine subspace does not necessarily contain it.
- ^ Some authors (such as Roman 2005) choose to start with this equivalence relation and derive the concrete shape of V/W from this.
- ^ This requirement implies that the topology gives rise to a uniform structure, Bourbaki 1989, ch. II
- ^ بالتباين المثلثي ل يتم توفيره من خلال متباينة منكوڤسكي. لأسباب فنية، في سياق الدوال، يتعين على المرء تحديد الدوال التي توافق في كل مكان تقريباً للحصول على معيار، وليس فقط شبه معيار.
- ^ "Many functions in of Lebesgue measure, being unbounded, cannot be integrated with the classical Riemann integral. So spaces of Riemann integrable functions would not be complete in the norm, and the orthogonal decomposition would not apply to them. This shows one of the advantages of Lebesgue integration.", Dudley 1989, §5.3, p. 125
- ^ For p ≠2, Lp(Ω) is not a Hilbert space.
- ^ A basis of a Hilbert space is not the same thing as a basis in the sense of linear algebra above.قالب:Huh For distinction, the latter is then called a Hamel basis.
- ^ Although the Fourier series is periodic, the technique can be applied to any L2 function on an interval by considering the function to be continued periodically outside the interval. See Kreyszig 1988, p. 601
- ^ That is to say (BSE-3 2001), the plane passing through the point of contact P such that the distance from a point P1 on the surface to the plane is infinitesimally small compared to the distance from P1 to P in the limit as P1 approaches P along the surface.
- ^ That is, there is a homeomorphism from π−1(U) to V × U which restricts to linear isomorphisms between fibers.
- ^ A line bundle, such as the tangent bundle of S1 is trivial if and only if there is a section that vanishes nowhere, see Husemoller 1994, Corollary 8.3. The sections of the tangent bundle are just vector fields.
Citations
- ^ أ ب "Comprehensive List of Algebra Symbols". Math Vault (in الإنجليزية الأمريكية). 2020-03-25. Retrieved 2020-08-23.
- ^ Roman 2005, ch. 1, p. 27
- ^ "5: Vector Spaces". Mathematics LibreTexts (in الإنجليزية). 2016-02-29. Retrieved 2020-08-23.
- ^ Weisstein, Eric W. "Vector Space". mathworld.wolfram.com (in الإنجليزية). Retrieved 2020-08-23.
- ^ van der Waerden 1993, Ch. 19
- ^ Bourbaki 1998, §II.1.1. Bourbaki calls the group homomorphisms f(a) homotheties.
- ^ Bourbaki 1969, ch. "Algèbre linéaire et algèbre multilinéaire", pp. 78–91.
- ^ Bolzano 1804.
- ^ Möbius 1827.
- ^ Hamilton 1853.
- ^ Grassmann 2000.
- ^ Peano 1888, ch. IX.
- ^ Banach 1922.
- ^ Dorier 1995, Moore 1995.
- ^ Lang 1987, ch. I.1
- ^ Lang 2002, ch. V.1
- ^ Lang 1993, ch. XII.3., p. 335
- ^ Lang 1987, ch. IX.1
- ^ Lang 1987, ch. VI.3.
- ^ Roman 2005, Theorem 1.9, p. 43
- ^ Blass 1984
- ^ Halpern 1966, pp. 670–673
- ^ Artin 1991, Theorem 3.3.13
- ^ Braun 1993, Th. 3.4.5, p. 291
- ^ Stewart 1975, Proposition 4.3, p. 52
- ^ Stewart 1975, Theorem 6.5, p. 74
- ^ Roman 2005, ch. 2, p. 45
- ^ Lang 1987, ch. IV.4, Corollary, p. 106
- ^ Lang 1987, Example IV.2.6
- ^ Lang 1987, ch. VI.6
- ^ Halmos 1974, p. 28, Ex. 9
- ^ Lang 1987, Theorem IV.2.1, p. 95
- ^ Roman 2005, Th. 2.5 and 2.6, p. 49
- ^ Lang 1987, ch. V.1
- ^ Lang 1987, ch. V.3., Corollary, p. 106
- ^ Lang 1987, Theorem VII.9.8, p. 198
- ^ Roman 2005, ch. 8, p. 135–156
- ^ Lang 1987, ch. IX.4
- ^ Roman 2005, ch. 8, p. 140.
- ^ Roman 2005, ch. 1, p. 29
- ^ Roman 2005, ch. 1, p. 35
- ^ Roman 2005, ch. 3, p. 64
- ^ Lang 1987, ch. IV.3.
- ^ Roman 2005, ch. 2, p. 48
- ^ Mac Lane 1998
- ^ Roman 2005, ch. 1, pp. 31–32
- ^ Lang 2002, ch. XVI.1
- ^ Roman 2005, Th. 14.3. انظر أيضاً Yoneda lemma.
- ^ Schaefer & Wolff 1999, pp. 204–205
- ^ Bourbaki 2004, ch. 2, p. 48
- ^ Roman 2005, ch. 9
- ^ Naber 2003, ch. 1.2
- ^ Treves 1967
- ^ Bourbaki 1987
- ^ Kreyszig 1989, §4.11-5
- ^ Kreyszig 1989, §1.5-5
- ^ Choquet 1966, Proposition III.7.2
- ^ Treves 1967, p. 34–36
- ^ Lang 1983, Cor. 4.1.2, p. 69
- ^ Treves 1967, ch. 11
- ^ Treves 1967, Theorem 11.2, p. 102
- ^ Evans 1998, ch. 5
- ^ Treves 1967, ch. 12
- ^ Dennery & Krzywicki 1996, p.190
- ^ Lang 1993, Th. XIII.6, p. 349
- ^ Lang 1993, Th. III.1.1
- ^ Choquet 1966, Lemma III.16.11
- ^ Kreyszig 1999, Chapter 11
- ^ Griffiths 1995, Chapter 1
- ^ Lang 1993, ch. XVII.3
- ^ Lang 2002, ch. III.1, p. 121
- ^ Eisenbud 1995, ch. 1.6
- ^ Varadarajan 1974
- ^ Lang 2002, ch. XVI.7
- ^ Lang 2002, ch. XVI.8
- ^ Luenberger 1997, §7.13
- ^ See representation theory and group representation.
- ^ Lang 1993, Ch. XI.1
- ^ Evans 1998, Th. 6.2.1
- ^ Folland 1992, p. 349 ff
- ^ Gasquet & Witomski 1999, p. 150
- ^ أ ب Gasquet & Witomski 1999, §4.5
- ^ Gasquet & Witomski 1999, p. 57
- ^ Loomis 1953, Ch. VII
- ^ Ashcroft & Mermin 1976, Ch. 5
- ^ Kreyszig 1988, p. 667
- ^ Fourier 1822
- ^ Gasquet & Witomski 1999, p. 67
- ^ Ifeachor & Jervis 2001, pp. 3–4, 11
- ^ Wallace 1992
- ^ Ifeachor & Jervis 2001, p. 132
- ^ Gasquet & Witomski 1999, §10.2
- ^ Ifeachor & Jervis 2001, pp. 307–310
- ^ Gasquet & Witomski 1999, §10.3
- ^ Schönhage & Strassen 1971
- ^ أ ب Spivak 1999, ch. 3
- ^ Jost 2005. See also Lorentzian manifold.
- ^ Misner, Thorne & Wheeler 1973, ch. 1.8.7, p. 222 and ch. 2.13.5, p. 325
- ^ Jost 2005, ch. 3.1
- ^ Varadarajan 1974, ch. 4.3, Theorem 4.3.27
- ^ Kreyszig 1991, §34, p. 108
- ^ Eisenberg & Guy 1979
- ^ Atiyah 1989
- ^ Artin 1991, ch. 12
- ^ Grillet, Pierre Antoine. Abstract algebra. Vol. 242. Springer Science & Business Media, 2007.
- ^ Meyer 2000, Example 5.13.5, p. 436
- ^ Meyer 2000, Exercise 5.13.15–17, p. 442
- ^ Coxeter 1987
References
Algebra
- Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-89871-510-1
- Blass, Andreas (1984), "Existence of bases implies the axiom of choice", Axiomatic set theory (Boulder, Colorado, 1983), Contemporary Mathematics, 31, Providence, R.I.: American Mathematical Society, pp. 31–33
- Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5, https://archive.org/details/matricesvectorsp0000brow
- Lang, Serge (1987), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6
- قالب:Lang Algebra
- Mac Lane, Saunders (1999), Algebra (3rd ed.), pp. 193–222, ISBN 978-0-8218-1646-2
- Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra, SIAM, ISBN 978-0-89871-454-8, http://www.matrixanalysis.com/
- Roman, Steven (2005), Advanced Linear Algebra, Graduate Texts in Mathematics, 135 (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-24766-3
- Spindler, Karlheinz (1993), Abstract Algebra with Applications: Volume 1: Vector spaces and groups, CRC, ISBN 978-0-8247-9144-5
- van der Waerden, Bartel Leendert (1993) (in de), Algebra (9th ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-56799-8
Analysis
- Bourbaki, Nicolas (1987), Topological vector spaces, Elements of mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-13627-9
- Bourbaki, Nicolas (2004), Integration I, Berlin, New York: Springer-Verlag, ISBN 978-3-540-41129-1
- Braun, Martin (1993), Differential equations and their applications: an introduction to applied mathematics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-97894-9
- BSE-3 (2001), "Tangent plane", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Choquet, Gustave (1966), Topology, Boston, MA: Academic Press
- Dennery, Philippe; Krzywicki, Andre (1996), Mathematics for Physicists, Courier Dover Publications, ISBN 978-0-486-69193-0
- Dudley, Richard M. (1989), Real analysis and probability, The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-10050-6
- Dunham, William (2005), The Calculus Gallery, Princeton University Press, ISBN 978-0-691-09565-3
- Evans, Lawrence C. (1998), Partial differential equations, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0772-9
- Folland, Gerald B. (1992), Fourier Analysis and Its Applications, Brooks-Cole, ISBN 978-0-534-17094-3
- Gasquet, Claude; Witomski, Patrick (1999), Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets, Texts in Applied Mathematics, New York: Springer-Verlag, ISBN 978-0-387-98485-8
- Ifeachor, Emmanuel C.; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach (2nd ed.), Harlow, Essex, England: Prentice-Hall (published 2002), ISBN 978-0-201-59619-9
- Krantz, Steven G. (1999), A Panorama of Harmonic Analysis, Carus Mathematical Monographs, Washington, DC: Mathematical Association of America, ISBN 978-0-88385-031-2
- Kreyszig, Erwin (1988), Advanced Engineering Mathematics (6th ed.), New York: John Wiley & Sons, ISBN 978-0-471-85824-9
- Kreyszig, Erwin (1989), Introductory functional analysis with applications, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-50459-7
- Lang, Serge (1983), Real analysis, Addison-Wesley, ISBN 978-0-201-14179-5
- Lang, Serge (1993), Real and functional analysis, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94001-4
- Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis, Toronto-New York–London: D. Van Nostrand Company, Inc., pp. x+190
- قالب:Narici Beckenstein Topological Vector Spaces
- قالب:Schaefer Wolff Topological Vector Spaces
- Treves, François (1967), Topological vector spaces, distributions and kernels, Boston, MA: Academic Press
Historical references
- Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)" (in fr), Fundamenta Mathematicae 3: 133–181, doi:, ISSN 0016-2736, http://matwbn.icm.edu.pl/ksiazki/fm/fm3/fm3120.pdf
- Bolzano, Bernard (1804) (in de), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry), http://dml.cz/handle/10338.dmlcz/400338
- Bourbaki, Nicolas (1969) (in fr), Éléments d'histoire des mathématiques (Elements of history of mathematics), Paris: Hermann
- Dorier, Jean-Luc (1995), "A general outline of the genesis of vector space theory", Historia Mathematica 22 (3): 227–261, doi:, http://archive-ouverte.unige.ch/unige:16642
- Fourier, Jean Baptiste Joseph (1822) (in fr), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, https://books.google.com/books?id=TDQJAAAAIAAJ
- Grassmann, Hermann (1844) (in de), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik, O. Wigand, https://books.google.com/books?id=bKgAAAAAMAAJ&pg=PA1, reprint: Grassmann, Hermann (2000), Kannenberg, L.C., ed., Extension Theory, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5
- Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy, http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=05230001&seq=9
- Möbius, August Ferdinand (1827) (in de), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry), http://mathdoc.emath.fr/cgi-bin/oeitem?id=OE_MOBIUS__1_1_0
- Moore, Gregory H. (1995), "The axiomatization of linear algebra: 1875–1940", Historia Mathematica 22 (3): 262–303, doi:
- Peano, Giuseppe (1888) (in it), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva, Turin
- Peano, G. (1901) Formulario mathematico: vct axioms via Internet Archive
Further references
- Ashcroft, Neil; Mermin, N. David (1976), Solid State Physics, Toronto: Thomson Learning, ISBN 978-0-03-083993-1, https://archive.org/details/solidstatephysic00ashc
- Atiyah, Michael Francis (1989), K-theory, Advanced Book Classics (2nd ed.), Addison-Wesley, ISBN 978-0-201-09394-0
- Bourbaki, Nicolas (1998), Elements of Mathematics : Algebra I Chapters 1-3, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64243-5
- Bourbaki, Nicolas (1989), General Topology. Chapters 1-4, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64241-1
- Coxeter, Harold Scott MacDonald (1987), Projective Geometry (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96532-1
- Eisenberg, Murray; Guy, Robert (1979), "A proof of the hairy ball theorem", The American Mathematical Monthly 86 (7): 572–574, doi:
- Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94269-8
- Goldrei, Derek (1996), Classic Set Theory: A guided independent study (1st ed.), London: Chapman and Hall, ISBN 978-0-412-60610-6
- Griffiths, David J. (1995), Introduction to Quantum Mechanics, Upper Saddle River, NJ: Prentice Hall, ISBN 978-0-13-124405-4
- Halmos, Paul R. (1974), Finite-dimensional vector spaces, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90093-3
- Halpern, James D. (Jun 1966), "Bases in Vector Spaces and the Axiom of Choice", Proceedings of the American Mathematical Society 17 (3): 670–673, doi:
- Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013), Calculus : Single and Multivariable (6 ed.), John Wiley & Sons, ISBN 978-0470-88861-2
- Husemoller, Dale (1994), Fibre Bundles (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94087-8
- Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (4th ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-25907-7
- Kreyszig, Erwin (1991), Differential geometry, New York: Dover Publications, pp. xiv+352, ISBN 978-0-486-66721-8
- Kreyszig, Erwin (1999), Advanced Engineering Mathematics (8th ed.), New York: John Wiley & Sons, ISBN 978-0-471-15496-9, https://archive.org/details/advancedengineer0008krey
- Luenberger, David (1997), Optimization by vector space methods, New York: John Wiley & Sons, ISBN 978-0-471-18117-0
- Mac Lane, Saunders (1998), Categories for the Working Mathematician (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-98403-2
- Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald (1973), Gravitation, W. H. Freeman, ISBN 978-0-7167-0344-0
- Naber, Gregory L. (2003), The geometry of Minkowski spacetime, New York: Dover Publications, ISBN 978-0-486-43235-9
- Schönhage, A.; Strassen, Volker (1971), "Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)" (in de), Computing 7 (3–4): 281–292, doi:, ISSN 0010-485X
- Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two), Houston, TX: Publish or Perish
- Stewart, Ian (1975), Galois Theory, Chapman and Hall Mathematics Series, London: Chapman and Hall, ISBN 978-0-412-10800-6, https://archive.org/details/galoistheory0000stew
- Varadarajan, V. S. (1974), Lie groups, Lie algebras, and their representations, Prentice Hall, ISBN 978-0-13-535732-3
- Wallace, G.K. (Feb 1992), "The JPEG still picture compression standard", IEEE Transactions on Consumer Electronics 38 (1): xviii–xxxiv, doi:, ISSN 0098-3063, http://www.csc.ncsu.edu/faculty/rhee/export/papers/TheJPEGStillPictureCompressionStandard.pdf, retrieved on 2017-10-25
- قالب:Weibel IHA
External links
- Hazewinkel, Michiel, ed. (2001), "Vector space", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104















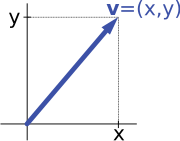



















































![{\displaystyle {\frac {a_{0}}{2}}+\sum _{m=1}^{\infty }\left[a_{m}\cos \left(mx\right)+b_{m}\sin \left(mx\right)\right].}](https://www.marefa.org/api/rest_v1/media/math/render/svg/b02fb26ebada4babaa1d88e20bb63e3b370c13b3)