مجموعة (رياضيات)
في الرياضيات، المجموعة (group)، هي فئة with an operation that satisfies the following constraints: the operation is associative and has an identity element, and every element of the set has an inverse element.
Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called (these properties characterize the integers in a unique way).
The concept of a group was elaborated for handling, in a unified way, many mathematical structures such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics.[1][2]
In geometry, groups arise naturally in the study of symmetries and geometric transformations: The symmetries of an object form a group, called the symmetry group of the object, and the transformations of a given type form a general group. Lie groups appear in symmetry groups in geometry, and also in the Standard Model of particle physics. The Poincaré group is a Lie group consisting of the symmetries of spacetime in special relativity. Point groups describe symmetry in molecular chemistry.
The concept of a group arose in the study of polynomial equations, starting with Évariste Galois in the 1830s, who introduced the term group (French: groupe) for the symmetry group of the roots of an equation, now called a Galois group. After contributions from other fields such as number theory and geometry, the group notion was generalized and firmly established around 1870. Modern group theory—an active mathematical discipline—studies groups in their own right. To explore groups, mathematicians have devised various notions to break groups into smaller, better-understandable pieces, such as subgroups, quotient groups and simple groups. In addition to their abstract properties, group theorists also study the different ways in which a group can be expressed concretely, both from a point of view of representation theory (that is, through the representations of the group) and of computational group theory. A theory has been developed for finite groups, which culminated with the classification of finite simple groups, completed in 2004. Since the mid-1980s, geometric group theory, which studies finitely generated groups as geometric objects, has become an active area in group theory.
| البنية الجبرية ← نظرية المجموعات نظرية المجموعات |
|---|
 |
| البنى الجبرية |
|---|
التعريف والتبيان
المثال الأول: الأعداد الصحيحة
One of the more familiar groups is the set of integers
- For all integers , and , one has . Expressed in words, adding to first, and then adding the result to gives the same final result as adding to the sum of and . This property is known as associativity.
- If is any integer, then and . Zero is called the identity element of addition because adding it to any integer returns the same integer.
- For every integer , there is an integer such that and . The integer is called the inverse element of the integer and is denoted .
The integers, together with the operation , form a mathematical object belonging to a broad class sharing similar structural aspects. To appropriately understand these structures as a collective, the following definition is developed.
التعريف
Richard Borcherds, Mathematicians: An Outer View of the Inner World[4]
A group is a non-empty set together with a binary operation on , here denoted "", that combines any two elements and of to form an element of , denoted , such that the following three requirements, known as group axioms, are satisfied:[5][6][7][أ]
- Associativity
- For all , , in , one has .
- Identity element
- There exists an element in such that, for every in , one has and .
- Such an element is unique (see below). It is called the identity element (or sometimes neutral element) of the group.
- Inverse element
- For each in , there exists an element in such that and , where is the identity element.
- For each , the element is unique (see below); it is called the inverse of and is commonly denoted .
التدوين والمصطلحات
Formally, a group is an ordered pair of a set and a binary operation on this set that satisfies the group axioms. The set is called the underlying set of the group, and the operation is called the group operation or the group law.
A group and its underlying set are thus two different mathematical objects. To avoid cumbersome notation, it is common to abuse notation by using the same symbol to denote both. This reflects also an informal way of thinking: that the group is the same as the set except that it has been enriched by additional structure provided by the operation.
For example, consider the set of real numbers , which has the operations of addition and multiplication . Formally, is a set, is a group, and is a field. But it is common to write to denote any of these three objects.
The additive group of the field is the group whose underlying set is and whose operation is addition. The multiplicative group of the field is the group whose underlying set is the set of nonzero real numbers and whose operation is multiplication.
More generally, one speaks of an additive group whenever the group operation is notated as addition; in this case, the identity is typically denoted , and the inverse of an element is denoted . Similarly, one speaks of a multiplicative group whenever the group operation is notated as multiplication; in this case, the identity is typically denoted , and the inverse of an element is denoted . In a multiplicative group, the operation symbol is usually omitted entirely, so that the operation is denoted by juxtaposition, instead of .
The definition of a group does not require that for all elements and in . If this additional condition holds, then the operation is said to be commutative, and the group is called an abelian group. It is a common convention that for an abelian group either additive or multiplicative notation may be used, but for a nonabelian group only multiplicative notation is used.
Several other notations are commonly used for groups whose elements are not numbers. For a group whose elements are functions, the operation is often function composition ; then the identity may be denoted id. In the more specific cases of geometric transformation groups, symmetry groups, permutation groups, and automorphism groups, the symbol is often omitted, as for multiplicative groups. Many other variants of notation may be encountered.
المثال الثاني: مجموعة تماثل
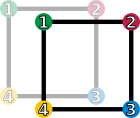
Two figures in the plane are congruent if one can be changed into the other using a combination of rotations, reflections, and translations. Any figure is congruent to itself. However, some figures are congruent to themselves in more than one way, and these extra congruences are called symmetries. A square has eight symmetries. These are:
- the identity operation leaving everything unchanged, denoted id;
- rotations of the square around its center by 90°, 180°, and 270° clockwise, denoted by , and , respectively;
- reflections about the horizontal and vertical middle line ( and ), or through the two diagonals ( and ).
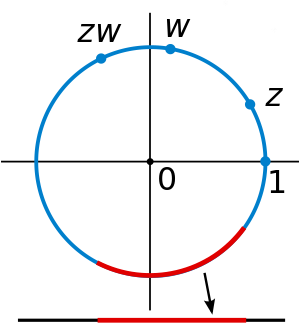
These symmetries are functions. Each sends a point in the square to the corresponding point under the symmetry. For example, sends a point to its rotation 90° clockwise around the square's center, and sends a point to its reflection across the square's vertical middle line. Composing two of these symmetries gives another symmetry. These symmetries determine a group called the dihedral group of degree four, denoted . The underlying set of the group is the above set of symmetries, and the group operation is function composition.[8] Two symmetries are combined by composing them as functions, that is, applying the first one to the square, and the second one to the result of the first application. The result of performing first and then is written symbolically from right to left as ("apply the symmetry after performing the symmetry "). This is the usual notation for composition of functions.
A Cayley table lists the results of all such compositions possible. For example, rotating by 270° clockwise () and then reflecting horizontally () is the same as performing a reflection along the diagonal (). Using the above symbols, highlighted in blue in the Cayley table:
| العناصر , , , and form a subgroup whose Cayley table is highlighted in red (upper left region). A left and right coset of this subgroup are highlighted in green (in the last row) and yellow (last column), respectively. The result of the composition , the symmetry , is highlighted in blue (below table center). | ||||||||
Given this set of symmetries and the described operation, the group axioms can be understood as follows.
Binary operation: Composition is a binary operation. That is, is a symmetry for any two symmetries and . For example,
Associativity: The associativity axiom deals with composing more than two symmetries: Starting with three elements , and of , there are two possible ways of using these three symmetries in this order to determine a symmetry of the square. One of these ways is to first compose and into a single symmetry, then to compose that symmetry with . The other way is to first compose and , then to compose the resulting symmetry with . These two ways must give always the same result, that is,
Identity element: The identity element is , as it does not change any symmetry when composed with it either on the left or on the right.
Inverse element: Each symmetry has an inverse: , the reflections , , , and the 180° rotation are their own inverse, because performing them twice brings the square back to its original orientation. The rotations and are each other's inverses, because rotating 90° and then rotation 270° (or vice versa) yields a rotation over 360° which leaves the square unchanged. This is easily verified on the table.
In contrast to the group of integers above, where the order of the operation is immaterial, it does matter in , as, for example, but . In other words, is not abelian.
التاريخ
The modern concept of an abstract group developed out of several fields of mathematics.[9][10][11] The original motivation for group theory was the quest for solutions of polynomial equations of degree higher than 4. The 19th-century French mathematician Évariste Galois, extending prior work of Paolo Ruffini and Joseph-Louis Lagrange, gave a criterion for the solvability of a particular polynomial equation in terms of the symmetry group of its roots (solutions). The elements of such a Galois group correspond to certain permutations of the roots. At first, Galois's ideas were rejected by his contemporaries, and published only posthumously.[12][13] More general permutation groups were investigated in particular by Augustin Louis Cauchy. Arthur Cayley's On the theory of groups, as depending on the symbolic equation (1854) gives the first abstract definition of a finite group.[14]
Geometry was a second field in which groups were used systematically, especially symmetry groups as part of Felix Klein's 1872 Erlangen program.[15] After novel geometries such as hyperbolic and projective geometry had emerged, Klein used group theory to organize them in a more coherent way. Further advancing these ideas, Sophus Lie founded the study of Lie groups in 1884.[16]
The third field contributing to group theory was number theory. Certain abelian group structures had been used implicitly in Carl Friedrich Gauss's number-theoretical work Disquisitiones Arithmeticae (1798), and more explicitly by Leopold Kronecker.[17] In 1847, Ernst Kummer made early attempts to prove Fermat's Last Theorem by developing groups describing factorization into prime numbers.[18]
The convergence of these various sources into a uniform theory of groups started with Camille Jordan's Traité des substitutions et des équations algébriques (1870).[19] Walther von Dyck (1882) introduced the idea of specifying a group by means of generators and relations, and was also the first to give an axiomatic definition of an "abstract group", in the terminology of the time.[20] As of the 20th century, groups gained wide recognition by the pioneering work of Ferdinand Georg Frobenius and William Burnside (who worked on representation theory of finite groups), Richard Brauer's modular representation theory and Issai Schur's papers.[21] The theory of Lie groups, and more generally locally compact groups was studied by Hermann Weyl, Élie Cartan and many others.[22] Its algebraic counterpart, the theory of algebraic groups, was first shaped by Claude Chevalley (from the late 1930s) and later by the work of Armand Borel and Jacques Tits.[23]
The University of Chicago's 1960–61 Group Theory Year brought together group theorists such as Daniel Gorenstein, John G. Thompson and Walter Feit, laying the foundation of a collaboration that, with input from numerous other mathematicians, led to the classification of finite simple groups, with the final step taken by Aschbacher and Smith in 2004. This project exceeded previous mathematical endeavours by its sheer size, in both length of proof and number of researchers. Research concerning this classification proof is ongoing.[24] Group theory remains a highly active mathematical branch,[ب] impacting many other fields, as the examples below illustrate.
Elementary consequences of the group axioms
Basic facts about all groups that can be obtained directly from the group axioms are commonly subsumed under elementary group theory.[25] For example, repeated applications of the associativity axiom show that the unambiguity of
Uniqueness of identity element
The group axioms imply that the identity element is unique; that is, there exists only one identity element: any two identity elements and of a group are equal, because the group axioms imply . It is thus customary to speak of the identity element of the group.[27]
Uniqueness of inverses
The group axioms also imply that the inverse of each element is unique: Let a group element have both and as inverses. Then
Therefore, it is customary to speak of the inverse of an element.[27]
Division
Given elements and of a group , there is a unique solution in to the equation , namely .[ت][28] It follows that for each in , the function that maps each to is a bijection; it is called left multiplication by or left translation by .
Similarly, given and , the unique solution to is . For each , the function that maps each to is a bijection called right multiplication by or right translation by .
Equivalent definition with relaxed axioms
The group axioms for identity and inverses may be "weakened" to assert only the existence of a left identity and left inverses. From these one-sided axioms, one can prove that the left identity is also a right identity and a left inverse is also a right inverse for the same element. Since they define exactly the same structures as groups, collectively the axioms are not weaker.[29]
In particular, assuming associativity and the existence of a left identity (that is, ) and a left inverse for each element (that is, ), one can show that every left inverse is also a right inverse of the same element as follows.[29] Indeed, one has
Similarly, the left identity is also a right identity:[29]
These proofs require all three axioms (associativity, existence of left identity and existence of left inverse). For a structure with a looser definition (like a semigroup) one may have, for example, that a left identity is not necessarily a right identity.
The same result can be obtained by only assuming the existence of a right identity and a right inverse.
However, only assuming the existence of a left identity and a right inverse (or vice versa) is not sufficient to define a group. For example, consider the set with the operator satisfying and . This structure does have a left identity (namely, ), and each element has a right inverse (which is for both elements). Furthermore, this operation is associative (since the product of any number of elements is always equal to the rightmost element in that product, regardless of the order in which these operations are done). However, is not a group, since it lacks a right identity.
Basic concepts
When studying sets, one uses concepts such as subset, function, and quotient by an equivalence relation. When studying groups, one uses instead subgroups, homomorphisms, and quotient groups. These are the analogues that take the group structure into account.[ث]
Group homomorphisms
Group homomorphisms[ج] are functions that respect group structure; they may be used to relate two groups. A homomorphism from a group to a group is a function such that
It would be natural to require also that respect identities, , and inverses, for all in . However, these additional requirements need not be included in the definition of homomorphisms, because they are already implied by the requirement of respecting the group operation.[30]
The identity homomorphism of a group is the homomorphism that maps each element of to itself. An inverse homomorphism of a homomorphism is a homomorphism such that and , that is, such that for all in and such that for all in . An isomorphism is a homomorphism that has an inverse homomorphism; equivalently, it is a bijective homomorphism. Groups and are called isomorphic if there exists an isomorphism . In this case, can be obtained from simply by renaming its elements according to the function ; then any statement true for is true for , provided that any specific elements mentioned in the statement are also renamed.
The collection of all groups, together with the homomorphisms between them, form a category, the category of groups.[31]
An injective homomorphism factors canonically as an isomorphism followed by an inclusion, for some subgroup of . Injective homomorphisms are the monomorphisms in the category of groups.
Subgroups
Informally, a subgroup is a group contained within a bigger one, : it has a subset of the elements of , with the same operation.[32] Concretely, this means that the identity element of must be contained in , and whenever and are both in , then so are and , so the elements of , equipped with the group operation on restricted to , indeed form a group. In this case, the inclusion map is a homomorphism.
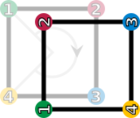
In the example of symmetries of a square, the identity and the rotations constitute a subgroup , highlighted in red in the Cayley table of the example: any two rotations composed are still a rotation, and a rotation can be undone by (i.e., is inverse to) the complementary rotations 270° for 90°, 180° for 180°, and 90° for 270°. The subgroup test provides a necessary and sufficient condition for a nonempty subset of a group to be a subgroup: it is sufficient to check that for all elements and in . Knowing a group's subgroups is important in understanding the group as a whole.[ح]
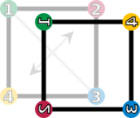
Given any subset of a group , the subgroup generated by consists of all products of elements of and their inverses. It is the smallest subgroup of containing .[33] In the example of symmetries of a square, the subgroup generated by and consists of these two elements, the identity element , and the element . Again, this is a subgroup, because combining any two of these four elements or their inverses (which are, in this particular case, these same elements) yields an element of this subgroup.
Cosets
In many situations it is desirable to consider two group elements the same if they differ by an element of a given subgroup. For example, in the symmetry group of a square, once any reflection is performed, rotations alone cannot return the square to its original position, so one can think of the reflected positions of the square as all being equivalent to each other, and as inequivalent to the unreflected positions; the rotation operations are irrelevant to the question whether a reflection has been performed. Cosets are used to formalize this insight: a subgroup determines left and right cosets, which can be thought of as translations of by an arbitrary group element . In symbolic terms, the left and right cosets of , containing an element , are
The left cosets of any subgroup form a partition of ; that is, the union of all left cosets is equal to and two left cosets are either equal or have an empty intersection.[35] The first case happens precisely when , i.e., when the two elements differ by an element of . Similar considerations apply to the right cosets of . The left cosets of may or may not be the same as its right cosets. If they are (that is, if all in satisfy ), then is said to be a normal subgroup.
In , the group of symmetries of a square, with its subgroup of rotations, the left cosets are either equal to , if is an element of itself, or otherwise equal to (highlighted in green in the Cayley table of ). The subgroup is normal, because and similarly for the other elements of the group. (In fact, in the case of , the cosets generated by reflections are all equal: .)
Quotient groups
Suppose that is a normal subgroup of a group , and
The elements of the quotient group are and . The group operation on the quotient is shown in the table. For example, . Both the subgroup and the quotient are abelian, but is not. Sometimes a group can be reconstructed from a subgroup and quotient (plus some additional data), by the semidirect product construction; is an example.
The first isomorphism theorem implies that any surjective homomorphism factors canonically as a quotient homomorphism followed by an isomorphism: . Surjective homomorphisms are the epimorphisms in the category of groups.
Presentations
Every group is isomorphic to a quotient of a free group, in many ways.
For example, the dihedral group is generated by the right rotation and the reflection in a vertical line (every element of is a finite product of copies of these and their inverses). Hence there is a surjective homomorphism from the free group on two generators to sending to and to . Elements in are called relations; examples include . In fact, it turns out that is the smallest normal subgroup of containing these three elements; in other words, all relations are consequences of these three. The quotient of the free group by this normal subgroup is denoted . This is called a presentation of by generators and relations, because the first isomorphism theorem for yields an isomorphism .[37]
A presentation of a group can be used to construct the Cayley graph, a graphical depiction of a discrete group.[38]
Examples and applications

Examples and applications of groups abound. A starting point is the group of integers with addition as group operation, introduced above. If instead of addition multiplication is considered, one obtains multiplicative groups. These groups are predecessors of important constructions in abstract algebra.
Groups are also applied in many other mathematical areas. Mathematical objects are often examined by associating groups to them and studying the properties of the corresponding groups. For example, Henri Poincaré founded what is now called algebraic topology by introducing the fundamental group.[39] By means of this connection, topological properties such as proximity and continuity translate into properties of groups.[خ]
Elements of the fundamental group of a topological space are equivalence classes of loops, where loops are considered equivalent if one can be smoothly deformed into another, and the group operation is "concatenation" (tracing one loop then the other). For example, as shown in the figure, if the topological space is the plane with one point removed, then loops which do not wrap around the missing point (blue) can be smoothly contracted to a single point and are the identity element of the fundamental group. A loop which wraps around the missing point times cannot be deformed into a loop which wraps times (with ), because the loop cannot be smoothly deformed across the hole, so each class of loops is characterized by its winding number around the missing point. The resulting group is isomorphic to the integers under addition.
In more recent applications, the influence has also been reversed to motivate geometric constructions by a group-theoretical background.[د] In a similar vein, geometric group theory employs geometric concepts, for example in the study of hyperbolic groups.[40] Further branches crucially applying groups include algebraic geometry and number theory.[41]
In addition to the above theoretical applications, many practical applications of groups exist. Cryptography relies on the combination of the abstract group theory approach together with algorithmical knowledge obtained in computational group theory, in particular when implemented for finite groups.[42] Applications of group theory are not restricted to mathematics; sciences such as physics, chemistry and computer science benefit from the concept.
Numbers
Many number systems, such as the integers and the rationals, enjoy a naturally given group structure. In some cases, such as with the rationals, both addition and multiplication operations give rise to group structures. Such number systems are predecessors to more general algebraic structures known as rings and fields. Further abstract algebraic concepts such as modules, vector spaces and algebras also form groups.
Integers
The group of integers under addition, denoted , has been described above. The integers, with the operation of multiplication instead of addition, do not form a group. The associativity and identity axioms are satisfied, but inverses do not exist: for example, is an integer, but the only solution to the equation in this case is , which is a rational number, but not an integer. Hence not every element of has a (multiplicative) inverse.[ذ]
Rationals
The desire for the existence of multiplicative inverses suggests considering fractions
Fractions of integers (with nonzero) are known as rational numbers.[ر] The set of all such irreducible fractions is commonly denoted . There is still a minor obstacle for , the rationals with multiplication, being a group: because zero does not have a multiplicative inverse (i.e., there is no such that ), is still not a group.
However, the set of all nonzero rational numbers does form an abelian group under multiplication, also denoted .[ز] Associativity and identity element axioms follow from the properties of integers. The closure requirement still holds true after removing zero, because the product of two nonzero rationals is never zero. Finally, the inverse of is , therefore the axiom of the inverse element is satisfied.
The rational numbers (including zero) also form a group under addition. Intertwining addition and multiplication operations yields more complicated structures called rings and – if division by other than zero is possible, such as in – fields, which occupy a central position in abstract algebra. Group theoretic arguments therefore underlie parts of the theory of those entities.[س]
Modular arithmetic
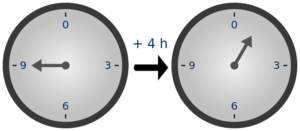
Modular arithmetic for a modulus defines any two elements and that differ by a multiple of to be equivalent, denoted by . Every integer is equivalent to one of the integers from to , and the operations of modular arithmetic modify normal arithmetic by replacing the result of any operation by its equivalent representative. Modular addition, defined in this way for the integers from to , forms a group, denoted as or , with as the identity element and as the inverse element of .
A familiar example is addition of hours on the face of a clock, where 12 rather than 0 is chosen as the representative of the identity. If the hour hand is on and is advanced hours, it ends up on , as shown in the illustration. This is expressed by saying that is congruent to "modulo " or, in symbols,
For any prime number , there is also the multiplicative group of integers modulo .[43] Its elements can be represented by to . The group operation, multiplication modulo , replaces the usual product by its representative, the remainder of division by . For example, for , the four group elements can be represented by . In this group, , because the usual product is equivalent to : when divided by it yields a remainder of . The primality of ensures that the usual product of two representatives is not divisible by , and therefore that the modular product is nonzero.[ش] The identity element is represented by , and associativity follows from the corresponding property of the integers. Finally, the inverse element axiom requires that given an integer not divisible by , there exists an integer such that
Cyclic groups
A cyclic group is a group all of whose elements are powers of a particular element .[46] In multiplicative notation, the elements of the group are
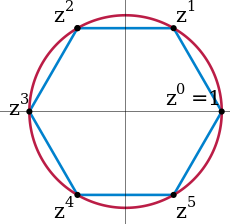
In the groups introduced above, the element is primitive, so these groups are cyclic. Indeed, each element is expressible as a sum all of whose terms are . Any cyclic group with elements is isomorphic to this group. A second example for cyclic groups is the group of th complex roots of unity, given by complex numbers satisfying . These numbers can be visualized as the vertices on a regular -gon, as shown in blue in the image for . The group operation is multiplication of complex numbers. In the picture, multiplying with corresponds to a counter-clockwise rotation by 60°.[47] From field theory, the group is cyclic for prime : for example, if , is a generator since , , , and .
Some cyclic groups have an infinite number of elements. In these groups, for every non-zero element , all the powers of are distinct; despite the name "cyclic group", the powers of the elements do not cycle. An infinite cyclic group is isomorphic to , the group of integers under addition introduced above.[48] As these two prototypes are both abelian, so are all cyclic groups.
The study of finitely generated abelian groups is quite mature, including the fundamental theorem of finitely generated abelian groups; and reflecting this state of affairs, many group-related notions, such as center and commutator, describe the extent to which a given group is not abelian.[49]
Symmetry groups

Symmetry groups are groups consisting of symmetries of given mathematical objects, principally geometric entities, such as the symmetry group of the square given as an introductory example above, although they also arise in algebra such as the symmetries among the roots of polynomial equations dealt with in Galois theory (see below).[51] Conceptually, group theory can be thought of as the study of symmetry.[ط] Symmetries in mathematics greatly simplify the study of geometrical or analytical objects. A group is said to act on another mathematical object if every group element can be associated to some operation on and the composition of these operations follows the group law. For example, an element of the (2,3,7) triangle group acts on a triangular tiling of the hyperbolic plane by permuting the triangles.[50] By a group action, the group pattern is connected to the structure of the object being acted on.
In chemistry, point groups describe molecular symmetries, while space groups describe crystal symmetries in crystallography. These symmetries underlie the chemical and physical behavior of these systems, and group theory enables simplification of quantum mechanical analysis of these properties.[52] For example, group theory is used to show that optical transitions between certain quantum levels cannot occur simply because of the symmetry of the states involved.[53]
Group theory helps predict the changes in physical properties that occur when a material undergoes a phase transition, for example, from a cubic to a tetrahedral crystalline form. An example is ferroelectric materials, where the change from a paraelectric to a ferroelectric state occurs at the Curie temperature and is related to a change from the high-symmetry paraelectric state to the lower symmetry ferroelectric state, accompanied by a so-called soft phonon mode, a vibrational lattice mode that goes to zero frequency at the transition.[54]
Such spontaneous symmetry breaking has found further application in elementary particle physics, where its occurrence is related to the appearance of Goldstone bosons.[55]
|

|

|
|
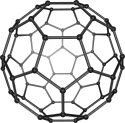
| Buckminsterfullerene displays icosahedral symmetry[56] |
Ammonia, NH3. Its symmetry group is of order 6, generated by a 120° rotation and a reflection.[57] | Cubane C8H8 features octahedral symmetry.[58] |
The tetrachloroplatinate(II) ion, [PtCl4]2− exhibits square-planar geometry |
Finite symmetry groups such as the Mathieu groups are used in coding theory, which is in turn applied in error correction of transmitted data, and in CD players.[59] Another application is differential Galois theory, which characterizes functions having antiderivatives of a prescribed form, giving group-theoretic criteria for when solutions of certain differential equations are well-behaved.[ظ] Geometric properties that remain stable under group actions are investigated in (geometric) invariant theory.[60]
General linear group and representation theory
Matrix groups consist of matrices together with matrix multiplication. The general linear group consists of all invertible -by- matrices with real entries.[61] Its subgroups are referred to as matrix groups or linear groups. The dihedral group example mentioned above can be viewed as a (very small) matrix group. Another important matrix group is the special orthogonal group . It describes all possible rotations in dimensions. Rotation matrices in this group are used in computer graphics.[62]
Representation theory is both an application of the group concept and important for a deeper understanding of groups.[63][64] It studies the group by its group actions on other spaces. A broad class of group representations are linear representations in which the group acts on a vector space, such as the three-dimensional Euclidean space . A representation of a group on an -dimensional real vector space is simply a group homomorphism from the group to the general linear group. This way, the group operation, which may be abstractly given, translates to the multiplication of matrices making it accessible to explicit computations.[ع]
A group action gives further means to study the object being acted on.[غ] On the other hand, it also yields information about the group. Group representations are an organizing principle in the theory of finite groups, Lie groups, algebraic groups and topological groups, especially (locally) compact groups.[63][65]
Galois groups
Galois groups were developed to help solve polynomial equations by capturing their symmetry features.[66][67] For example, the solutions of the quadratic equation are given by
Modern Galois theory generalizes the above type of Galois groups by shifting to field theory and considering field extensions formed as the splitting field of a polynomial. This theory establishes—via the fundamental theorem of Galois theory—a precise relationship between fields and groups, underlining once again the ubiquity of groups in mathematics.[70]
Finite groups
A group is called finite if it has a finite number of elements. The number of elements is called the order of the group.[71] An important class is the symmetric groups , the groups of permutations of objects. For example, the symmetric group on 3 letters is the group of all possible reorderings of the objects. The three letters ABC can be reordered into ABC, ACB, BAC, BCA, CAB, CBA, forming in total 6 (factorial of 3) elements. The group operation is composition of these reorderings, and the identity element is the reordering operation that leaves the order unchanged. This class is fundamental insofar as any finite group can be expressed as a subgroup of a symmetric group for a suitable integer , according to Cayley's theorem. Parallel to the group of symmetries of the square above, can also be interpreted as the group of symmetries of an equilateral triangle.
The order of an element in a group is the least positive integer such that , where represents
More sophisticated counting techniques, for example, counting cosets, yield more precise statements about finite groups: Lagrange's Theorem states that for a finite group the order of any finite subgroup divides the order of . The Sylow theorems give a partial converse.
The dihedral group of symmetries of a square is a finite group of order 8. In this group, the order of is 4, as is the order of the subgroup that this element generates. The order of the reflection elements etc. is 2. Both orders divide 8, as predicted by Lagrange's theorem. The groups of multiplication modulo a prime have order .
Finite abelian groups
Any finite abelian group is isomorphic to a product of finite cyclic groups; this statement is part of the fundamental theorem of finitely generated abelian groups.
Any group of prime order is isomorphic to the cyclic group (a consequence of Lagrange's theorem). Any group of order is abelian, isomorphic to or . But there exist nonabelian groups of order ; the dihedral group of order above is an example.[72]
Simple groups
When a group has a normal subgroup other than and itself, questions about can sometimes be reduced to questions about and . A nontrivial group is called simple if it has no such normal subgroup. Finite simple groups are to finite groups as prime numbers are to positive integers: they serve as building blocks, in a sense made precise by the Jordan–Hölder theorem.
Classification of finite simple groups
Computer algebra systems have been used to list all groups of order up to 2000.[ف] But classifying all finite groups is a problem considered too hard to be solved.
The classification of all finite simple groups was a major achievement in contemporary group theory. There are several infinite families of such groups, as well as 26 "sporadic groups" that do not belong to any of the families. The largest sporadic group is called the monster group. The monstrous moonshine conjectures, proved by Richard Borcherds, relate the monster group to certain modular functions.[73]
The gap between the classification of simple groups and the classification of all groups lies in the extension problem.[74]
Groups with additional structure
An equivalent definition of group consists of replacing the "there exist" part of the group axioms by operations whose result is the element that must exist. So, a group is a set equipped with a binary operation (the group operation), a unary operation (which provides the inverse) and a nullary operation, which has no operand and results in the identity element. Otherwise, the group axioms are exactly the same. This variant of the definition avoids existential quantifiers and is used in computing with groups and for computer-aided proofs.
This way of defining groups lends itself to generalizations such as the notion of group object in a category. Briefly, this is an object with morphisms that mimic the group axioms.[75]
Topological groups
Some topological spaces may be endowed with a group law. In order for the group law and the topology to interweave well, the group operations must be continuous functions; informally, and must not vary wildly if and vary only a little. Such groups are called topological groups, and they are the group objects in the category of topological spaces.[76] The most basic examples are the group of real numbers under addition and the group of nonzero real numbers under multiplication. Similar examples can be formed from any other topological field, such as the field of complex numbers or the field of p-adic numbers. These examples are locally compact, so they have Haar measures and can be studied via harmonic analysis. Other locally compact topological groups include the group of points of an algebraic group over a local field or adele ring; these are basic to number theory[77] Galois groups of infinite algebraic field extensions are equipped with the Krull topology, which plays a role in infinite Galois theory.[78] A generalization used in algebraic geometry is the étale fundamental group.[79]
Lie groups
A Lie group is a group that also has the structure of a differentiable manifold; informally, this means that it looks locally like a Euclidean space of some fixed dimension.[80] Again, the definition requires the additional structure, here the manifold structure, to be compatible: the multiplication and inverse maps are required to be smooth.
A standard example is the general linear group introduced above: it is an open subset of the space of all -by- matrices, because it is given by the inequality
Lie groups are of fundamental importance in modern physics: Noether's theorem links continuous symmetries to conserved quantities.[82] Rotation, as well as translations in space and time, are basic symmetries of the laws of mechanics. They can, for instance, be used to construct simple models—imposing, say, axial symmetry on a situation will typically lead to significant simplification in the equations one needs to solve to provide a physical description.[ق] Another example is the group of Lorentz transformations, which relate measurements of time and velocity of two observers in motion relative to each other. They can be deduced in a purely group-theoretical way, by expressing the transformations as a rotational symmetry of Minkowski space. The latter serves—in the absence of significant gravitation—as a model of spacetime in special relativity.[83] The full symmetry group of Minkowski space, i.e., including translations, is known as the Poincaré group. By the above, it plays a pivotal role in special relativity and, by implication, for quantum field theories.[84] Symmetries that vary with location are central to the modern description of physical interactions with the help of gauge theory. An important example of a gauge theory is the Standard Model, which describes three of the four known fundamental forces and classifies all known elementary particles.[85]
Generalizations
| بنى شبيهة الزمرة | |||||
|---|---|---|---|---|---|
| Totality[1] | Associativity | حيادي | Divisibility | Commutativity | |
| Semicategory | غير مطلوب | مطلوب | غير مطلوب | غير مطلوب | غير مطلوب |
| Category | غير مطلوب | مطلوب | مطلوب | غير مطلوب | غير مطلوب |
| Groupoid | غير مطلوب | مطلوب | مطلوب | مطلوب | غير مطلوب |
| Magma | مطلوب | غير مطلوب | غير مطلوب | غير مطلوب | غير مطلوب |
| Quasigroup | مطلوب | غير مطلوب | غير مطلوب | مطلوب | غير مطلوب |
| Loop | مطلوب | غير مطلوب | مطلوب | مطلوب | غير مطلوب |
| شبه زمرة | مطلوب | مطلوب | غير مطلوب | غير مطلوب | غير مطلوب |
| مونويد | مطلوب | مطلوب | مطلوب | غير مطلوب | غير مطلوب |
| زمرة | مطلوب | مطلوب | مطلوب | مطلوب | غير مطلوب |
| زمرة أبيلية | مطلوب | مطلوب | مطلوب | مطلوب | مطلوب |
| ^α Closure, which is used in many sources, is an equivalent axiom to totality, though defined differently. | |||||
More general structures may be defined by relaxing some of the axioms defining a group.[31][86][87] The table gives a list of several structures generalizing groups.
For example, if the requirement that every element has an inverse is eliminated, the resulting algebraic structure is called a monoid. The natural numbers (including zero) under addition form a monoid, as do the nonzero integers under multiplication . Adjoining inverses of all elements of the monoid produces a group , and likewise adjoining inverses to any (abelian) monoid produces a group known as the Grothendieck group of .
A group can be thought of as a small category with one object in which every morphism is an isomorphism: given such a category, the set is a group; conversely, given a group , one can build a small category with one object in which . More generally, a groupoid is any small category in which every morphism is an isomorphism. In a groupoid, the set of all morphisms in the category is usually not a group, because the composition is only partially defined: is defined only when the source of matches the target of . Groupoids arise in topology (for instance, the fundamental groupoid) and in the theory of stacks.
Finally, it is possible to generalize any of these concepts by replacing the binary operation with an n-ary operation (i.e., an operation taking n arguments, for some nonnegative integer n). With the proper generalization of the group axioms, this gives a notion of n-ary group.[88]
| Set | Natural numbers | Integers | Rational numbers Real numbers Complex numbers |
Integers modulo 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Operation | + | × | + | × | + | − | × | ÷ | + | × |
| Closed | Yes | Yes | Yes | Yes | Yes | Yes | Yes | No | Yes | Yes |
| Identity | 0 | 1 | 0 | 1 | 0 | N/A | 1 | N/A | 0 | 1 |
| Inverse | N/A | N/A | N/A | N/A | () |
N/A | 0, 2, 1, respectively | N/A, 1, 2, respectively | ||
| Associative | Yes | Yes | Yes | Yes | Yes | No | Yes | No | Yes | Yes |
| Commutative | Yes | Yes | Yes | Yes | Yes | No | Yes | No | Yes | Yes |
| Structure | monoid | monoid | abelian group | monoid | abelian group | quasi-group | monoid | quasi-group | abelian group | monoid |
انظر أيضاً
الهوامش
- ^ Some authors include an additional axiom referred to as the closure under the operation "⋅", which means that a ⋅ b is an element of G for every a and b in G. This condition is subsumed by requiring "⋅" to be a binary operation on G. See Lang 2002.
- ^ The MathSciNet database of mathematics publications lists 1,779 research papers on group theory and its generalizations written in 2020 alone. See MathSciNet 2021.
- ^ One usually avoids using fraction notation b/a unless G is abelian, because of the ambiguity of whether it means a−1 ⋅ b or b ⋅ a−1.)
- ^ See, for example, Lang 2002, Lang 2005, Herstein 1996 and Herstein 1975.
- ^ The word homomorphism derives from Greek ὁμός—the same and μορφή—structure. See Schwartzman 1994, p. 108.
- ^ However, a group is not determined by its lattice of subgroups. See Suzuki 1951.
- ^ See the Seifert–Van Kampen theorem for an example.
- ^ An example is group cohomology of a group which equals the singular cohomology of its classifying space, see Weibel 1994, §8.2.
- ^ Elements which do have multiplicative inverses are called units, see Lang 2002, §II.1.
- ^ The transition from the integers to the rationals by including fractions is generalized by the field of fractions.
- ^ The same is true for any field F instead of Q. See Lang 2005, §III.1.
- ^ For example, a finite subgroup of the multiplicative group of a field is necessarily cyclic. See Lang 2002, Theorem IV.1.9. The notions of torsion of a module and simple algebras are other instances of this principle.
- ^ The stated property is a possible definition of prime numbers. See Prime element.
- ^ For example, the Diffie–Hellman protocol uses the discrete logarithm. See Gollmann 2011, §15.3.2.
- ^ The additive notation for elements of a cyclic group would be t ⋅ a, where t is in Z.
- ^ More rigorously, every group is the symmetry group of some graph; see Frucht's theorem, Frucht 1939.
- ^ More precisely, the monodromy action on the vector space of solutions of the differential equations is considered. See Kuga 1993, pp. 105–113.
- ^ This was crucial to the classification of finite simple groups, for example. See Aschbacher 2004.
- ^ See, for example, Schur's Lemma for the impact of a group action on simple modules. A more involved example is the action of an absolute Galois group on étale cohomology.
- ^ Up to isomorphism, there are about 49 billion groups of order up to 2000. See Besche, Eick & O'Brien 2001.
- ^ See Schwarzschild metric for an example where symmetry greatly reduces the complexity of physical systems.
المصادر
- ^ Herstein 1975, §2.
- ^ Hall 1967, §1.1: "The idea of a group is one which pervades the whole of mathematics both pure and applied.".
- ^ Lang 2005, App. 2.
- ^ Cook 2009, p. 24.
- ^ Artin 2018, §2.2.
- ^ Lang 2002, p. 3, I.§1 and p. 7, I.§2.
- ^ Lang 2005, II.§1.
- ^ Herstein 1975, §2.6.
- ^ Wussing 2007.
- ^ Kleiner 1986.
- ^ Smith 1906.
- ^ Galois 1908.
- ^ Kleiner 1986, p. 202.
- ^ Cayley 1889.
- ^ Wussing 2007, §III.2.
- ^ Lie 1973.
- ^ Kleiner 1986, p. 204.
- ^ Wussing 2007, §I.3.4.
- ^ Jordan 1870.
- ^ von Dyck 1882.
- ^ Curtis 2003.
- ^ Mackey 1976.
- ^ Borel 2001.
- ^ Solomon 2018.
- ^ Ledermann 1953, §1.2.
- ^ Ledermann 1973, §I.1.
- ^ أ ب Lang 2005, §II.1.
- ^ Artin 2018, p. 40.
- ^ أ ب ت Lang 2002, §I.2.
- ^ Lang 2005, §II.3.
- ^ أ ب Mac Lane 1998.
- ^ Lang 2005, §II.1.
- ^ Ledermann 1973, §II.12.
- ^ Lang 2005, §II.4.
- ^ Lang 2002, §I.2.
- ^ Lang 2005, §II.4.
- ^ Lang 2002, §I.2.
- ^ Magnus, Karrass & Solitar 2004, §1.6.
- ^ Hatcher 2002, Chapter I.
- ^ Coornaert, Delzant & Papadopoulos 1990.
- ^ For example, class groups and Picard groups; see Neukirch 1999, in particular §§I.12 and I.13
- ^ Seress 1997.
- ^ Lang 2005, Chapter VII.
- ^ Rosen 2000, (Theorem 2.1).
- ^ Lang 2005, §VIII.1.
- ^ Lang 2005, §II.1.
- ^ Lang 2005, §II.2.
- ^ Lang 2005, §II.1 (example 11).
- ^ Lang 2002, §I.5.
- ^ أ ب Ellis 2019.
- ^ Weyl 1952.
- ^ Conway et al. 2001. See also Bishop 1993
- ^ Weyl 1950, pp. 197–202.
- ^ Dove 2003.
- ^ Zee 2010, p. 228.
- ^ Chancey & O'Brien 2021, pp. 15, 16.
- ^ Simons 2003, §4.2.1.
- ^ Eliel, Wilen & Mander 1994, p. 82.
- ^ Welsh 1989.
- ^ Mumford, Fogarty & Kirwan 1994.
- ^ Lay 2003.
- ^ Kuipers 1999.
- ^ أ ب Fulton & Harris 1991.
- ^ Serre 1977.
- ^ Rudin 1990.
- ^ Robinson 1996, p. viii.
- ^ Artin 1998.
- ^ Lang 2002, Chapter VI (see in particular p. 273 for concrete examples).
- ^ Lang 2002, (Theorem VI.7.2).
- ^ Stewart 2015, §12.1.
- ^ Kurzweil & Stellmacher 2004, p. 3.
- ^ Artin 2018, Proposition 6.4.3. See also Lang 2002, p. 77 for similar results.
- ^ Ronan 2007.
- ^ Aschbacher 2004, p. 737.
- ^ Awodey 2010, §4.1.
- ^ Husain 1966.
- ^ Neukirch 1999.
- ^ Shatz 1972.
- ^ Milne 1980.
- ^ Warner 1983.
- ^ Borel 1991.
- ^ Goldstein 1980.
- ^ Weinberg 1972.
- ^ Naber 2003.
- ^ Zee 2010.
- ^ Denecke & Wismath 2002.
- ^ Romanowska & Smith 2002.
- ^ Dudek 2001.
المراجع
مراجع عامة
- Artin, Michael (2018), Algebra, Prentice Hall, ISBN 978-0-13-468960-9, Chapter 2 contains an undergraduate-level exposition of the notions covered in this article.
- Cook, Mariana R. (2009), Mathematicians: An Outer View of the Inner World, Princeton, N.J.: Princeton University Press, ISBN 978-0-691-13951-7, https://books.google.com/books?id=06h8NT77OgMC&q=Richard+Ewen+Borcherds&pg=PA24
- Hall, G. G. (1967), Applied Group Theory, American Elsevier Publishing Co., Inc., New York, an elementary introduction.
- Herstein, Israel Nathan (1996), Abstract Algebra (3rd ed.), Upper Saddle River, NJ: Prentice Hall Inc., ISBN 978-0-13-374562-7.
- Herstein, Israel Nathan (1975), Topics in Algebra (2nd ed.), Lexington, Mass.: Xerox College Publishing.
- قالب:Lang Algebra
- Lang, Serge (2005), Undergraduate Algebra (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-22025-3.
- Ledermann, Walter (1953), Introduction to the Theory of Finite Groups, Oliver and Boyd, Edinburgh and London.
- Ledermann, Walter (1973), Introduction to Group Theory, New York: Barnes and Noble, OCLC 795613.
- Robinson, Derek John Scott (1996), A Course in the Theory of Groups, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94461-6.
مراجع متخصصة
- Artin, Emil (1998), Galois Theory, New York: Dover Publications, ISBN 978-0-486-62342-9.
- Aschbacher, Michael (2004), "The status of the classification of the finite simple groups", Notices of the American Mathematical Society 51 (7): 736–740, https://www.ams.org/notices/200407/fea-aschbacher.pdf.
- Awodey, Steve (2010), Category Theory, Oxford University Press, ISBN 978-0-19-958736-0
- Behler, Florian; Wickleder, Mathias S.; Christoffers, Jens (2014), "Biphenyl and bimesityl tetrasulfonic acid – new linker molecules for coordination polymers", Arkivoc 2015 (2): 64–75, doi:
- Bersuker, Isaac (2006), The Jahn–Teller Effect, Cambridge University Press, ISBN 0-521-82212-2, https://archive.org/details/jahntellereffect0000bers/page/2.
- Besche, Hans Ulrich; Eick, Bettina; O'Brien, E. A. (2001), "The groups of order at most 2000", Electronic Research Announcements of the American Mathematical Society 7: 1–4, doi:, https://www.ams.org/era/2001-07-01/S1079-6762-01-00087-7/home.html.
- Bishop, David H. L. (1993), Group Theory and Chemistry, New York: Dover Publications, ISBN 978-0-486-67355-4.
- Borel, Armand (1991), Linear Algebraic Groups, Graduate Texts in Mathematics, 126 (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-97370-8.
- Carter, Roger W. (1989), Simple Groups of Lie Type, New York: John Wiley & Sons, ISBN 978-0-471-50683-6.
- Chancey, C. C.; O'Brien, M. C. M. (2021), The Jahn–Teller Effect in C60 and Other Icosahedral Complexes, Princeton University Press, ISBN 978-0-691-22534-0
- Conway, John Horton; Delgado Friedrichs, Olaf; Huson, Daniel H.; Thurston, William P. (2001), "On three-dimensional space groups", Beiträge zur Algebra und Geometrie 42 (2): 475–507.
- Coornaert, M.; Delzant, T.; Papadopoulos, A. (1990) (in fr), Géométrie et théorie des groupes [Geometry and Group Theory], Lecture Notes in Mathematics, 1441, Berlin, New York: Springer-Verlag, ISBN 978-3-540-52977-4.
- Denecke, Klaus; Wismath, Shelly L. (2002), Universal Algebra and Applications in Theoretical Computer Science, London: CRC Press, ISBN 978-1-58488-254-1.
- Dove, Martin T (2003), Structure and Dynamics: An Atomic View of Materials, Oxford University Press, p. 265, ISBN 0-19-850678-3.
- Dudek, Wiesław A. (2001), "On some old and new problems in n-ary groups", Quasigroups and Related Systems 8: 15–36, https://ibn.idsi.md/sites/default/files/imag_file/15-36_On%20some%20old%20and%20new%20problems%20in%20n-ary%20groups.pdf.
- Eliel, Ernest; Wilen, Samuel; Mander, Lewis (1994), Stereochemistry of Organic Compounds, Wiley, ISBN 978-0-471-01670-0
- Ellis, Graham (2019), "6.4 Triangle groups", An Invitation to Computational Homotopy, Oxford University Press, pp. 441–444, doi:, ISBN 978-0-19-883298-0.
- Frucht, R. (1939), "Herstellung von Graphen mit vorgegebener abstrakter Gruppe [Construction of graphs with prescribed group]" (in de), Compositio Mathematica 6: 239–50, http://www.numdam.org/numdam-bin/fitem?id=CM_1939__6__239_0.
- Fulton, William; Harris, Joe (1991), Representation Theory: A First Course, Graduate Texts in Mathematics, Readings in Mathematics, 129, New York: Springer-Verlag, ISBN 978-0-387-97495-8
- Goldstein, Herbert (1980), Classical Mechanics (2nd ed.), Reading, MA: Addison-Wesley Publishing, pp. 588–596, ISBN 0-201-02918-9.
- Gollmann, Dieter (2011), Computer Security (2nd ed.), West Sussex, England: John Wiley & Sons, Ltd., ISBN 978-0-470-74115-3
- Hatcher, Allen (2002), Algebraic Topology, Cambridge University Press, ISBN 978-0-521-79540-1, http://www.math.cornell.edu/~hatcher/AT/ATpage.html.
- Husain, Taqdir (1966), Introduction to Topological Groups, Philadelphia: W.B. Saunders Company, ISBN 978-0-89874-193-3
- Jahn, H.; Teller, E. (1937), "Stability of polyatomic molecules in degenerate electronic states. I. Orbital degeneracy", Proceedings of the Royal Society A 161 (905): 220–235, doi:, Bibcode: 1937RSPSA.161..220J.
- Kuipers, Jack B. (1999), Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace, and Virtual Reality, Princeton University Press, ISBN 978-0-691-05872-6, Bibcode: 1999qrsp.book.....K.
- Kuga, Michio (1993), Galois' Dream: Group Theory and Differential Equations, Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-3688-3, https://archive.org/details/galoisdreamgroup0000kuga.
- Kurzweil, Hans; Stellmacher, Bernd (2004), The Theory of Finite Groups, Universitext, Berlin, New York: Springer-Verlag, ISBN 978-0-387-40510-0.
- Lay, David (2003), Linear Algebra and Its Applications, Addison-Wesley, ISBN 978-0-201-70970-4.
- Mac Lane, Saunders (1998), Categories for the Working Mathematician (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-98403-2.
- Magnus, Wilhelm; Karrass, Abraham; Solitar, Donald (2004), Combinatorial Group Theory: Presentations of Groups in Terms of Generators and Relations, Courier, ISBN 978-0-486-43830-6, https://books.google.com/books?id=1LW4s1RDRHQC&pg=PR2
- MathSciNet (2021), List of papers reviewed on MathSciNet on "Group theory and its generalizations" (MSC code 20), published in 2020, https://mathscinet.ams.org/mathscinet/search/publications.html?pg4=AUCN&s4=&co4=AND&pg5=TI&s5=&co5=AND&pg6=PC&s6=20&co6=AND&pg7=ALLF&s7=&co7=AND&dr=pubyear&yrop=eq&arg3=2020&yearRangeFirst=&yearRangeSecond=&pg8=ET&s8=All&review_format=html&Submit=Suche, retrieved on 14 May 2021
- Michler, Gerhard (2006), Theory of Finite Simple Groups, Cambridge University Press, ISBN 978-0-521-86625-5.
- Milne, James S. (1980), Étale Cohomology, Princeton University Press, ISBN 978-0-691-08238-7, https://archive.org/details/etalecohomology00miln
- Mumford, David; Fogarty, J.; Kirwan, F. (1994), Geometric Invariant Theory, 34 (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-56963-3.
- Naber, Gregory L. (2003), The Geometry of Minkowski Spacetime, New York: Dover Publications, ISBN 978-0-486-43235-9.
- Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften, 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8
- Romanowska, A. B.; Smith, J. D. H. (2002), Modes, World Scientific, ISBN 978-981-02-4942-7.
- Ronan, Mark (2007), Symmetry and the Monster: The Story of One of the Greatest Quests of Mathematics, Oxford University Press, ISBN 978-0-19-280723-6.
- Rosen, Kenneth H. (2000), Elementary Number Theory and its Applications (4th ed.), Addison-Wesley, ISBN 978-0-201-87073-2.
- Rudin, Walter (1990), Fourier Analysis on Groups, Wiley Classics, Wiley-Blackwell, ISBN 0-471-52364-X.
- Seress, Ákos (1997), "An Introduction to Computational Group Theory", Notices of the American Mathematical Society 44 (6): 671–679, https://www.ams.org/notices/199706/seress.pdf.
- Serre, Jean-Pierre (1977), Linear Representations of Finite Groups, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90190-9, https://archive.org/details/linearrepresenta1977serr.
- Schwartzman, Steven (1994), The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English, Mathematical Association of America, ISBN 978-0-88385-511-9.
- Shatz, Stephen S. (1972), Profinite Groups, Arithmetic, and Geometry, Princeton University Press, ISBN 978-0-691-08017-8
- Simons, Jack (2003), An Introduction to Theoretical Chemistry, Cambridge University Press, ISBN 978-0-521-53047-7
- Solomon, Ronald (2018), "The classification of finite simple groups: A progress report", Notices of the AMS 65 (6): 1, doi:
- Stewart, Ian (2015), Galois Theory (4th ed.), CRC Press, ISBN 978-1-4822-4582-0
- Suzuki, Michio (1951), "On the lattice of subgroups of finite groups", Transactions of the American Mathematical Society 70 (2): 345–371, doi:.
- Warner, Frank (1983), Foundations of Differentiable Manifolds and Lie Groups, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90894-6.
- قالب:Weibel IHA
- Weinberg, Steven (1972), Gravitation and Cosmology, New York: John Wiley & Sons, ISBN 0-471-92567-5, https://archive.org/details/gravitationcosmo00stev_0.
- Welsh, Dominic (1989), Codes and Cryptography, Oxford: Clarendon Press, ISBN 978-0-19-853287-3.
- Weyl, Hermann (1952), Symmetry, Princeton University Press, ISBN 978-0-691-02374-8.
- Zee, A. (2010), Quantum Field Theory in a Nutshell (second ed.), Princeton, N.J.: Princeton University Press, ISBN 978-0-691-14034-6, OCLC 768477138
مراجع تاريخية
- Borel, Armand (2001), Essays in the History of Lie Groups and Algebraic Groups, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0288-5
- Cayley, Arthur (1889), The Collected Mathematical Papers of Arthur Cayley, II (1851–1860), Cambridge University Press, http://www.hti.umich.edu/cgi/t/text/pageviewer-idx?c=umhistmath;cc=umhistmath;rgn=full%20text;idno=ABS3153.0001.001;didno=ABS3153.0001.001;view=image;seq=00000140.
- O'Connor, John J.; Robertson, Edmund F., "The development of group theory", MacTutor History of Mathematics archive, University of St Andrews.
- Curtis, Charles W. (2003), Pioneers of Representation Theory: Frobenius, Burnside, Schur, and Brauer, History of Mathematics, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2677-5.
- von Dyck, Walther (1882), "Gruppentheoretische Studien (Group-theoretical studies)" (in de), Mathematische Annalen 20 (1): 1–44, doi:, http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0020&DMDID=DMDLOG_0007&L=1.
- Galois, Évariste (1908), Tannery, Jules, ed. (in fr), Manuscrits de Évariste Galois [Évariste Galois' Manuscripts], Paris: Gauthier-Villars, http://quod.lib.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=AAN9280 (Galois work was first published by Joseph Liouville in 1843).
- Jordan, Camille (1870) (in fr), Traité des substitutions et des équations algébriques [Study of Substitutions and Algebraic Equations], Paris: Gauthier-Villars, https://archive.org/details/traitdessubstit00jordgoog.
- Kleiner, Israel (1986), "The evolution of group theory: A brief survey", Mathematics Magazine 59 (4): 195–215, doi:.
- Lie, Sophus (1973) (in de), Gesammelte Abhandlungen. Band 1 [Collected papers. Volume 1], New York: Johnson Reprint Corp..
- Mackey, George Whitelaw (1976), The Theory of Unitary Group Representations, University of Chicago Press
- Smith, David Eugene (1906), History of Modern Mathematics, Mathematical Monographs, No. 1, https://www.gutenberg.org/ebooks/8746.
- Weyl, Hermann (1950), The Theory of Groups and Quantum Mechanics, Dover, ISBN 978-0-486-60269-1.
- Wussing, Hans (2007), The Genesis of the Abstract Group Concept: A Contribution to the History of the Origin of Abstract Group Theory, New York: Dover Publications, ISBN 978-0-486-45868-7.