جذر دالة
- هذه المقالة عن جذور التوابع. لجذور الأعداد اطلع على جذر عدد.
في الرياضيات، يعرف جذر دالة f على أنه العنصر x من المجال الذي يحقق المعادلة التي تنعدم فيها الدالة f كما يلي:
مثلاً التابع المعطى بالصيغة التالية:
له جذر يساوي 3 لأن .
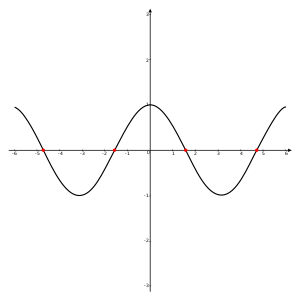
إذا كان التابع ممثل بمجموعة الأعداد الحقيقية، فإن جذوره هي نقاط تقاطع مخطط التابع مع محور السينات x، وهو ما يطلق عليه نقطة قطع محور السينات.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
