تطبيق خطي

"Linear transformation" تحوّل إلى هنا. لمطالعة fractional linear transformations، انظر Möbius transformation.

يجب ألا يـُخلـَط بينها وبين linear function.

في الرياضيات، التطبيق الخطي linear map (المسمى أيضاً التعيين الخطي، أو التحويل الخطي، أو تشاكل فضاء متجه، أو في بعض السياقات دالة خطية) هي تعيين $V\to W$ بين فضائين متجهين للحفاظ على عمليات إضافة المتجهات و الضرب العددي. يتم استخدام نفس الأسماء ونفس التعريف أيضاً للحالة الأكثر عمومية لـ الوحدات على الحلقات؛ انظر تشاكل وحدة.

إذا كان التطبيق الخطي عبارة عن تقابل فإنها تسمى تساوي الشكل. في الحالة التي يكون فيها $V=W$، يسمى التطبيق الخطي (خطياً) إندومورفية. أحياناً يشير المصطلح العامل الخطي إلى هذه الحالة، ولكن يمكن أن يكون لمصطلح "العامل الخطي" معانٍ مختلفة لمصطلحات مختلفة: على سبيل المثال، يمكن استخدامه للتأكيد على أن $V$ و$W$ هما مسافات متجهة حقيقية (ليس بالضرورة مع $V=W$), أو يمكن استخدامها للتأكيد على أن $V$ هو فضاء دالة، وهو اصطلاح شائع في التحليل الدالي.أحيانًا يكون للمصطلح نظم خطية نفس معنى التطبيق الخطي، بينما في التحليل ليس كذلك.

تطبيق خطي من V إلى W دائماً تعين أصل V إلى أصل W. علاوة على ذلك، فإنه يقوم بتعيين فضاء خطي جزئي في V على فضاءات فرعية خطية في W (ربما ذات بعد أقل);على سبيل المثال، تقوم بتعيين المستوى من خلال الأصل في V إلى إما مستوى من خلال الأصل في W، و خط من خلال الأصل في W، أو مجرد الأصل في W. غالباً ما يمكن تمثيل التطبيق الخطي على أنه مصفوفات، وتشمل الأمثلة البسيطة الدوران والانعكاس في التحويلات الخطية.

في لغة نظرية التصنيفات، التطبيق الخطي هو انحفاظ الشكل في الفضاءات المتجهة.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 Definition and first consequences

Let $V$ and $W$ be vector spaces over the same field $K$. A function $f:V\to W$ is said to be a linear map if for any two vectors ${\textstyle \mathbf {u} ,\mathbf {v} \in V}$ and any scalar $c\in K$ the following two conditions are satisfied:

Additivity / operation of addition

$f(\mathbf {u} +\mathbf {v} )=f(\mathbf {u} )+f(\mathbf {v} )$

Homogeneity of degree 1 / operation of scalar multiplication

$f(c\mathbf {u} )=cf(\mathbf {u} )$

Thus, a linear map is said to be operation preserving. In other words, it does not matter whether the linear map is applied before (the right hand sides of the above examples) or after (the left hand sides of the examples) the operations of addition and scalar multiplication.

By the associativity of the addition operation denoted as +, for any vectors ${\textstyle \mathbf {u} _{1},\ldots ,\mathbf {u} _{n}\in V}$ and scalars ${\textstyle c_{1},\ldots ,c_{n}\in K,}$ the following equality holds:

$$f(c_{1}\mathbf {u} _{1}+\cdots +c_{n}\mathbf {u} _{n})=c_{1}f(\mathbf {u} _{1})+\cdots +c_{n}f(\mathbf {u} _{n}).$$

Denoting the zero elements of the vector spaces $V$ and $W$ by ${\textstyle \mathbf {0} _{V}}$ and ${\textstyle \mathbf {0} _{W}}$ respectively, it follows that ${\textstyle f(\mathbf {0} _{V})=\mathbf {0} _{W}.}$ Let $c=0$ and ${\textstyle \mathbf {v} \in V}$ in the equation for homogeneity of degree 1:

$$f(\mathbf {0} _{V})=f(0\mathbf {v} )=0f(\mathbf {v} )=\mathbf {0} _{W}.$$

Occasionally, $V$ and $W$ can be vector spaces over different fields. It is then necessary to specify which of these ground fields is being used in the definition of "linear". If $V$ and $W$ are spaces over the same field $K$ as above, then we talk about $K$-linear maps. For example, the conjugation of complex numbers is an $\mathbb {R}$-linear map $\mathbb {C} \to \mathbb {C}$, but it is not $\mathbb {C}$-linear, where $\mathbb {R}$ and $\mathbb {C}$ are symbols representing the sets of real numbers and complex numbers, respectively.

A linear map $V\to K$ with $K$ viewed as a one-dimensional vector space over itself is called a linear functional.

These statements generalize to any left-module ${\textstyle {}_{R}M}$ over a ring $R$ without modification, and to any right-module upon reversing of the scalar multiplication.

 Examples

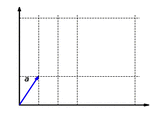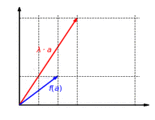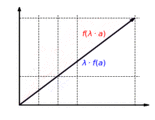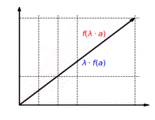
• A prototypical example that gives linear maps their name is a function $f:\mathbb {R} \to \mathbb {R} :x\mapsto cx$, of which the graph is a line through the origin.
• More generally, any homothety ${\textstyle \mathbf {v} \mapsto c\mathbf {v} }$ where $c$ centered in the origin of a vector space is a linear map.
• The zero map ${\textstyle \mathbf {x} \mapsto \mathbf {0} }$ between two vector spaces (over the same field) is linear.
• The identity map on any module is a linear operator.
• For real numbers, the map ${\textstyle x\mapsto x^{2}}$ is not linear.
• For real numbers, the map ${\textstyle x\mapsto x+1}$ is not linear (but is an affine transformation).
• If $A$ is a $m\times n$ real matrix, then $A$ defines a linear map from $\mathbb {R} ^{n}$ to $\mathbb {R} ^{m}$ by sending a column vector $\mathbf {x} \in \mathbb {R} ^{n}$ to the column vector $A\mathbf {x} \in \mathbb {R} ^{m}$. Conversely, any linear map between finite-dimensional vector spaces can be represented in this manner; see the § Matrices, below.
• If ${\textstyle f:V\to W}$ is an isometry between real normed spaces such that ${\textstyle f(0)=0}$ then $f$ is a linear map. This result is not necessarily true for complex normed space.
• Differentiation defines a linear map from the space of all differentiable functions to the space of all functions. It also defines a linear operator on the space of all smooth functions (a linear operator is a linear endomorphism, that is a linear map where the domain and codomain of it is the same). An example is
  $${\frac {d}{dx}}\left(c_{1}f_{1}(x)+c_{2}f_{2}(x)+\cdots +c_{n}f_{n}(x)\right)=c_{1}{\frac {df_{1}(x)}{dx}}+c_{2}{\frac {df_{2}(x)}{dx}}+\cdots +c_{n}{\frac {df_{n}(x)}{dx}}.$$
• A definite integral over some interval I is a linear map from the space of all real-valued integrable functions on I to $\mathbb {R}$. For example,
  $$\int _{a}^{b}{\left[c_{1}f_{1}(x)+c_{2}f_{2}(x)+\dots +c_{n}f_{n}(x)\right]dx}={c_{1}\int _{a}^{b}f_{1}(x)\,dx}+{c_{2}\int _{a}^{b}f_{2}(x)\,dx}+\cdots +{c_{n}\int _{a}^{b}f_{n}(x)\,dx}.$$
• An indefinite integral (or antiderivative) with a fixed integration starting point defines a linear map from the space of all real-valued integrable functions on $\mathbb {R}$ to the space of all real-valued, differentiable functions on $\mathbb {R}$. Without a fixed starting point, the antiderivative maps to the quotient space of the differentiable functions by the linear space of constant functions.
• If $V$ and $W$ are finite-dimensional vector spaces over a field F, of respective dimensions m and n, then the function that maps linear maps ${\textstyle f:V\to W}$ to n × m matrices in the way described in § Matrices (below) is a linear map, and even a linear isomorphism.
• The expected value of a random variable (which is in fact a function, and as such a element of a vector space) is linear, as for random variables $X$ and $Y$ we have $E[X+Y]=E[X]+E[Y]$ and $E[aX]=aE[X]$, but the variance of a random variable is not linear.

• 

  The function ${\textstyle f:\mathbb {R} ^{2}\to \mathbb {R} ^{2}}$ with ${\textstyle f(x,y)=(2x,y)}$ is a linear map. This function scales the ${\textstyle x}$ component of a vector by the factor ${\textstyle 2}$.

• 

  The function ${\textstyle f(x,y)=(2x,y)}$ is additive: It doesn't matter whether vectors are first added and then mapped or whether they are mapped and finally added: ${\textstyle f(\mathbf {a} +\mathbf {b} )=f(\mathbf {a} )+f(\mathbf {b} )}$

• 

  The function ${\textstyle f(x,y)=(2x,y)}$ is homogeneous: It doesn't matter whether a vector is first scaled and then mapped or first mapped and then scaled: ${\textstyle f(\lambda \mathbf {a} )=\lambda f(\mathbf {a} )}$

 Matrices

المقالة الرئيسية: Transformation matrix

If $V$ and $W$ are finite-dimensional vector spaces and a basis is defined for each vector space, then every linear map from $V$ to $W$ can be represented by a matrix. This is useful because it allows concrete calculations. Matrices yield examples of linear maps: if $A$ is a real $m\times n$ matrix, then $f(\mathbf {x} )=A\mathbf {x}$ describes a linear map $\mathbb {R} ^{n}\to \mathbb {R} ^{m}$ (see Euclidean space).

Let $\{{\mathbf {v}}_{1},\ldots ,{\mathbf {v}}_{n}\}$ be a basis for $V$. Then every vector ${\mathbf {v}}\in V$ is uniquely determined by the coefficients ${\mathbf {c}}_{1},\ldots ,{\mathbf {c}}_{n}$ in the field $\mathbb {R} ^{n}$:

$$c_{1}\mathbf {v} _{1}+\cdots +c_{n}\mathbf {v} _{n}.$$

If ${\textstyle f:V\to W}$ is a linear map,

$$f\left(c_{1}\mathbf {v} _{1}+\cdots +c_{n}\mathbf {v} _{n}\right)=c_{1}f\left(\mathbf {v} _{1}\right)+\cdots +c_{n}f\left(\mathbf {v} _{n}\right),$$

which implies that the function f is entirely determined by the vectors $f({\mathbf {v}}_{1}),\ldots ,f({\mathbf {v}}_{n})$. Now let $\{{\mathbf {w}}_{1},\ldots ,{\mathbf {w}}_{m}\}$ be a basis for $W$. Then we can represent each vector $f({\mathbf {v}}_{j})$ as

$$f\left(\mathbf {v} _{j}\right)=a_{1j}\mathbf {w} _{1}+\cdots +a_{mj}\mathbf {w} _{m}.$$

Thus, the function $f$ is entirely determined by the values of $a_{ij}$. If we put these values into an $m\times n$ matrix $M$, then we can conveniently use it to compute the vector output of $f$ for any vector in $V$. To get $M$, every column $j$ of $M$ is a vector

$${\begin{pmatrix}a_{1j}\\\vdots \\a_{mj}\end{pmatrix}}$$

corresponding to $f({\mathbf {v}}_{j})$ as defined above. To define it more clearly, for some column $j$ that corresponds to the mapping $f({\mathbf {v}}_{j})$,

$$\mathbf {M} ={\begin{pmatrix}\ \cdots &a_{1j}&\cdots \ \\&\vdots &\\&a_{mj}&\end{pmatrix}}$$

where $M$ is the matrix of $f$. In other words, every column $j=1,\ldots ,n$ has a corresponding vector $f({\mathbf {v}}_{j})$ whose coordinates $a_{1j}+\cdots +a_{mj}$ are the elements of column $j$. A single linear map may be represented by many matrices. This is because the values of the elements of a matrix depend on the bases chosen.

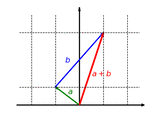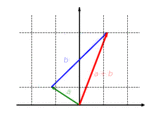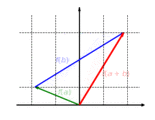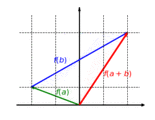
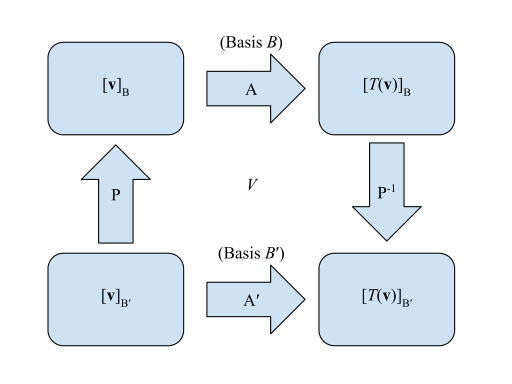
The matrices of a linear transformation can be represented visually:

1. Matrix for ${\textstyle T}$ relative to ${\textstyle B}$: ${\textstyle A}$
2. Matrix for ${\textstyle T}$ relative to ${\textstyle B'}$: ${\textstyle A'}$
3. Transition matrix from ${\textstyle B'}$ to ${\textstyle B}$: ${\textstyle P}$
4. Transition matrix from ${\textstyle B}$ to ${\textstyle B'}$: ${\textstyle P^{-1}}$

The relationship between matrices in a linear transformation

Such that starting in the bottom left corner ${\textstyle \left[\mathbf {v} \right]_{B'}}$ and looking for the bottom right corner ${\textstyle \left[T\left(\mathbf {v} \right)\right]_{B'}}$, one would left-multiply—that is, ${\textstyle A'\left[\mathbf {v} \right]_{B'}=\left[T\left(\mathbf {v} \right)\right]_{B'}}$. The equivalent method would be the "longer" method going clockwise from the same point such that ${\textstyle \left[\mathbf {v} \right]_{B'}}$ is left-multiplied with ${\textstyle P^{-1}AP}$, or ${\textstyle P^{-1}AP\left[\mathbf {v} \right]_{B'}=\left[T\left(\mathbf {v} \right)\right]_{B'}}$.

 Examples in two dimensions

In two-dimensional space R² linear maps are described by 2 × 2 matrices. These are some examples:

• rotation
  • by 90 degrees counterclockwise:
    $$\mathbf {A} ={\begin{pmatrix}0&-1\\1&0\end{pmatrix}}$$
  • by an angle θ counterclockwise:
    $$\mathbf {A} ={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}}$$
• reflection
  • through the x axis:
    $$\mathbf {A} ={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}$$
  • through the y axis:
    $$\mathbf {A} ={\begin{pmatrix}-1&0\\0&1\end{pmatrix}}$$
  • through a line making an angle θ with the origin:
    $$\mathbf {A} ={\begin{pmatrix}\cos {2\theta }&\sin {2\theta }\\\sin {2\theta }&-\cos {2\theta }\end{pmatrix}}$$
• scaling by 2 in all directions:
  $$\mathbf {A} ={\begin{pmatrix}2&0\\0&2\end{pmatrix}}=2\mathbf {I}$$
• horizontal shear mapping:
  $$\mathbf {A} ={\begin{pmatrix}1&m\\0&1\end{pmatrix}}$$
• squeeze mapping:
  $$\mathbf {A} ={\begin{pmatrix}k&0\\0&{\frac {1}{k}}\end{pmatrix}}$$
• projection onto the y axis:
  $$\mathbf {A} ={\begin{pmatrix}0&0\\0&1\end{pmatrix}}.$$

 Vector space of linear maps

The composition of linear maps is linear: if $f:V\to W$ and ${\textstyle g:W\to Z}$ are linear, then so is their composition ${\textstyle g\circ f:V\to Z}$. It follows from this that the class of all vector spaces over a given field K, together with K-linear maps as morphisms, forms a category.

The inverse of a linear map, when defined, is again a linear map.

If ${\textstyle f_{1}:V\to W}$ and ${\textstyle f_{2}:V\to W}$ are linear, then so is their pointwise sum $f_{1}+f_{2}$, which is defined by $(f_{1}+f_{2})(\mathbf {x} )=f_{1}(\mathbf {x} )+f_{2}(\mathbf {x} )$.

If ${\textstyle f:V\to W}$ is linear and ${\textstyle \alpha }$ is an element of the ground field ${\textstyle K}$, then the map ${\textstyle \alpha f}$, defined by ${\textstyle (\alpha f)(\mathbf {x} )=\alpha (f(\mathbf {x} ))}$, is also linear.

Thus the set ${\textstyle {\mathcal {L}}(V,W)}$ of linear maps from ${\textstyle V}$ to ${\textstyle W}$ itself forms a vector space over ${\textstyle K}$, sometimes denoted ${\textstyle \operatorname {Hom} (V,W)}$. Furthermore, in the case that ${\textstyle V=W}$, this vector space, denoted ${\textstyle \operatorname {End} (V)}$, is an associative algebra under composition of maps, since the composition of two linear maps is again a linear map, and the composition of maps is always associative. This case is discussed in more detail below.

Given again the finite-dimensional case, if bases have been chosen, then the composition of linear maps corresponds to the matrix multiplication, the addition of linear maps corresponds to the matrix addition, and the multiplication of linear maps with scalars corresponds to the multiplication of matrices with scalars.

 Endomorphisms and automorphisms

المقالة الرئيسية: Endomorphism and Automorphism

A linear transformation ${\textstyle f:V\to V}$ is an endomorphism of ${\textstyle V}$; the set of all such endomorphisms ${\textstyle \operatorname {End} (V)}$ together with addition, composition and scalar multiplication as defined above forms an associative algebra with identity element over the field ${\textstyle K}$ (and in particular a ring). The multiplicative identity element of this algebra is the identity map ${\textstyle \operatorname {id} :V\to V}$.

An endomorphism of ${\textstyle V}$ that is also an isomorphism is called an automorphism of ${\textstyle V}$. The composition of two automorphisms is again an automorphism, and the set of all automorphisms of ${\textstyle V}$ forms a group, the automorphism group of ${\textstyle V}$ which is denoted by ${\textstyle \operatorname {Aut} (V)}$ or ${\textstyle \operatorname {GL} (V)}$. Since the automorphisms are precisely those endomorphisms which possess inverses under composition, ${\textstyle \operatorname {Aut} (V)}$ is the group of units in the ring ${\textstyle \operatorname {End} (V)}$.

If ${\textstyle V}$ has finite dimension ${\textstyle n}$, then ${\textstyle \operatorname {End} (V)}$ is isomorphic to the associative algebra of all ${\textstyle n\times n}$ matrices with entries in ${\textstyle K}$. The automorphism group of ${\textstyle V}$ is isomorphic to the general linear group ${\textstyle \operatorname {GL} (n,K)}$ of all ${\textstyle n\times n}$ invertible matrices with entries in ${\textstyle K}$.

 Kernel, image and the rank–nullity theorem

المقالة الرئيسية: Kernel (linear algebra), Image (mathematics), and Rank of a matrix

If ${\textstyle f:V\to W}$ is linear, we define the kernel and the image or range of ${\textstyle f}$ by

$${\begin{aligned}\ker(f)&=\{\,\mathbf {x} \in V:f(\mathbf {x} )=\mathbf {0} \,\}\\\operatorname {im} (f)&=\{\,\mathbf {w} \in W:\mathbf {w} =f(\mathbf {x} ),\mathbf {x} \in V\,\}\end{aligned}}$$

${\textstyle \ker(f)}$ is a subspace of ${\textstyle V}$ and ${\textstyle \operatorname {im} (f)}$ is a subspace of ${\textstyle W}$. The following dimension formula is known as the rank–nullity theorem:

$$\dim(\ker(f))+\dim(\operatorname {im} (f))=\dim(V).$$

The number ${\textstyle \dim(\operatorname {im} (f))}$ is also called the rank of ${\textstyle f}$ and written as ${\textstyle \operatorname {rank} (f)}$, or sometimes, ${\textstyle \rho (f)}$; the number ${\textstyle \dim(\ker(f))}$ is called the nullity of ${\textstyle f}$ and written as ${\textstyle \operatorname {null} (f)}$ or ${\textstyle \nu (f)}$. If ${\textstyle V}$ and ${\textstyle W}$ are finite-dimensional, bases have been chosen and ${\textstyle f}$ is represented by the matrix ${\textstyle A}$, then the rank and nullity of ${\textstyle f}$ are equal to the rank and nullity of the matrix ${\textstyle A}$, respectively.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 Cokernel

المقالة الرئيسية: Cokernel

A subtler invariant of a linear transformation ${\textstyle f:V\to W}$ is the cokernel, which is defined as

$$\operatorname {coker} (f):=W/f(V)=W/\operatorname {im} (f).$$

This is the dual notion to the kernel: just as the kernel is a subspace of the domain, the co-kernel is a quotient space of the target. Formally, one has the exact sequence

$$0\to \ker(f)\to V\to W\to \operatorname {coker} (f)\to 0.$$

These can be interpreted thus: given a linear equation f(v) = w to solve,

• the kernel is the space of solutions to the homogeneous equation f(v) = 0, and its dimension is the number of degrees of freedom in the space of solutions, if it is not empty;
• the co-kernel is the space of constraints that the solutions must satisfy, and its dimension is the maximal number of independent constraints.

The dimension of the co-kernel and the dimension of the image (the rank) add up to the dimension of the target space. For finite dimensions, this means that the dimension of the quotient space W/f(V) is the dimension of the target space minus the dimension of the image.

As a simple example, consider the map f: R² → R², given by f(x, y) = (0, y). Then for an equation f(x, y) = (a, b) to have a solution, we must have a = 0 (one constraint), and in that case the solution space is (x, b) or equivalently stated, (0, b) + (x, 0), (one degree of freedom). The kernel may be expressed as the subspace (x, 0) < V: the value of x is the freedom in a solution – while the cokernel may be expressed via the map W → R, ${\textstyle (a,b)\mapsto (a)}$: given a vector (a, b), the value of a is the obstruction to there being a solution.

An example illustrating the infinite-dimensional case is afforded by the map f: R^∞ → R^∞, ${\textstyle \left\{a_{n}\right\}\mapsto \left\{b_{n}\right\}}$ with b₁ = 0 and b_{n + 1} = a_n for n > 0. Its image consists of all sequences with first element 0, and thus its cokernel consists of the classes of sequences with identical first element. Thus, whereas its kernel has dimension 0 (it maps only the zero sequence to the zero sequence), its co-kernel has dimension 1. Since the domain and the target space are the same, the rank and the dimension of the kernel add up to the same sum as the rank and the dimension of the co-kernel (${\textstyle \aleph _{0}+0=\aleph _{0}+1}$), but in the infinite-dimensional case it cannot be inferred that the kernel and the co-kernel of an endomorphism have the same dimension (0 ≠ 1). The reverse situation obtains for the map h: R^∞ → R^∞, ${\textstyle \left\{a_{n}\right\}\mapsto \left\{c_{n}\right\}}$ with c_n = a_{n + 1}. Its image is the entire target space, and hence its co-kernel has dimension 0, but since it maps all sequences in which only the first element is non-zero to the zero sequence, its kernel has dimension 1.

 Index

For a linear operator with finite-dimensional kernel and co-kernel, one may define index as:

$$\operatorname {ind} (f):=\dim(\ker(f))-\dim(\operatorname {coker} (f)),$$

namely the degrees of freedom minus the number of constraints.

For a transformation between finite-dimensional vector spaces, this is just the difference dim(V) − dim(W), by rank–nullity. This gives an indication of how many solutions or how many constraints one has: if mapping from a larger space to a smaller one, the map may be onto, and thus will have degrees of freedom even without constraints. Conversely, if mapping from a smaller space to a larger one, the map cannot be onto, and thus one will have constraints even without degrees of freedom.

The index of an operator is precisely the Euler characteristic of the 2-term complex 0 → V → W → 0. In operator theory, the index of Fredholm operators is an object of study, with a major result being the Atiyah–Singer index theorem.

 Algebraic classifications of linear transformations

No classification of linear maps could be exhaustive. The following incomplete list enumerates some important classifications that do not require any additional structure on the vector space.

Let V and W denote vector spaces over a field F and let T: V → W be a linear map.

Monomorphism

T is said to be injective or a monomorphism if any of the following equivalent conditions are true:

1. T is one-to-one as a map of sets.
2. ker T = {0_V}
3. dim(ker T) = 0
4. T is monic or left-cancellable, which is to say, for any vector space U and any pair of linear maps R: U → V and S: U → V, the equation TR = TS implies R = S.
5. T is left-invertible, which is to say there exists a linear map S: W → V such that ST is the identity map on V.

Epimorphism

T is said to be surjective or an epimorphism if any of the following equivalent conditions are true:

1. T is onto as a map of sets.
2. coker T = {0_W}
3. T is epic or right-cancellable, which is to say, for any vector space U and any pair of linear maps R: W → U and S: W → U, the equation RT = ST implies R = S.
4. T is right-invertible, which is to say there exists a linear map S: W → V such that TS is the identity map on W.

Isomorphism

T is said to be an isomorphism if it is both left- and right-invertible. This is equivalent to T being both one-to-one and onto (a bijection of sets) or also to T being both epic and monic, and so being a bimorphism.

If T: V → V is an endomorphism, then:

• If, for some positive integer n, the n-th iterate of T, Tⁿ, is identically zero, then T is said to be nilpotent.
• If T² = T, then T is said to be idempotent
• If T = kI, where k is some scalar, then T is said to be a scaling transformation or scalar multiplication map; see scalar matrix.

 Change of basis

المقالة الرئيسية: Basis (linear algebra) and Change of basis

Given a linear map which is an endomorphism whose matrix is A, in the basis B of the space it transforms vector coordinates [u] as [v] = A[u]. As vectors change with the inverse of B (vectors are contravariant) its inverse transformation is [v] = B[v'].

Substituting this in the first expression

$$B\left[v'\right]=AB\left[u'\right]$$

hence

$$\left[v'\right]=B^{-1}AB\left[u'\right]=A'\left[u'\right].$$

Therefore, the matrix in the new basis is A′ = B⁻¹AB, being B the matrix of the given basis.

Therefore, linear maps are said to be 1-co- 1-contra-variant objects, or type (1, 1) tensors.

 Continuity

المقالة الرئيسية: Continuous linear operator and Discontinuous linear map

A linear transformation between topological vector spaces, for example normed spaces, may be continuous. If its domain and codomain are the same, it will then be a continuous linear operator. A linear operator on a normed linear space is continuous if and only if it is bounded, for example, when the domain is finite-dimensional. An infinite-dimensional domain may have discontinuous linear operators.

An example of an unbounded, hence discontinuous, linear transformation is differentiation on the space of smooth functions equipped with the supremum norm (a function with small values can have a derivative with large values, while the derivative of 0 is 0). For a specific example, sin(nx)/n converges to 0, but its derivative cos(nx) does not, so differentiation is not continuous at 0 (and by a variation of this argument, it is not continuous anywhere).

 Applications

A specific application of linear maps is for geometric transformations, such as those performed in computer graphics, where the translation, rotation and scaling of 2D or 3D objects is performed by the use of a transformation matrix. Linear mappings also are used as a mechanism for describing change: for example in calculus correspond to derivatives; or in relativity, used as a device to keep track of the local transformations of reference frames.

Another application of these transformations is in compiler optimizations of nested-loop code, and in parallelizing compiler techniques.

 See also

• Antilinear map
• Bent function
• Bounded operator
• Continuous linear operator
• Linear functional
• Linear isometry

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 Bibliography

• Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.
• Bronshtein, I. N.; Semendyayev, K. A. (2004). Handbook of Mathematics (4th ed.). New York: Springer-Verlag. ISBN 3-540-43491-7.
• Halmos, Paul Richard (1974) [1958]. Finite-Dimensional Vector Spaces (2nd ed.). Springer. ISBN 0-387-90093-4.
• Horn, Roger A.; Johnson, Charles R. (2013). Matrix Analysis (Second ed.). Cambridge University Press. ISBN 978-0-521-83940-2.
• Katznelson, Yitzhak; Katznelson, Yonatan R. (2008). A (Terse) Introduction to Linear Algebra. American Mathematical Society. ISBN 978-0-8218-4419-9.
• Lang, Serge (1987), Linear Algebra (Third ed.), New York: Springer-Verlag, ISBN 0-387-96412-6 
• قالب:Rudin Walter Functional Analysis
• Rudin, Walter (1976). Principles of Mathematical Analysis. Walter Rudin Student Series in Advanced Mathematics (3rd ed.). New York: McGraw–Hill. ISBN 978-0-07-054235-8.
• قالب:Rudin Walter Functional Analysis
• قالب:Schaefer Wolff Topological Vector Spaces
• قالب:Swartz An Introduction to Functional Analysis
• Tu, Loring W. (2011). An Introduction to Manifolds (2nd ed.). Springer. ISBN 978-0-8218-4419-9.
• قالب:Wilansky Modern Methods in Topological Vector Spaces