السباعي
| Regular heptagon | |
|---|---|
 A regular heptagon | |
| النوع | مضلع منتظم |
| الأضلاع والرؤوس | {{{p7 جانب}}} |
| رمز شلفلي | {{{p7-شلفلي}}} |
| مخططات كوكستر-دنكن | |
| مجموعة التماثل | Dihedral (D7), order 2×7 |
| الزاوية الداخلية (الدرجات) | ≈128.571° |
| الخصائص | Convex, cyclic, equilateral, isogonal, isotoxal |
السباعي Heptagon المنتظم: هو مضلع محدب يتكون من اتحاد سبعة قطع مستقيمة متساوية الطول، وزواياه السبعة متساوية القياس. ومن المعلوم أيضا أنه يستحيل إنشاء السياعي المنتظم باستخدام المسطرة و الفرجار.
السباعي المنتظم
regular heptagon, in which all sides and all angles are equal, has internal angles of 5π/7 radians (1284⁄7 degrees). Its Schläfli symbol is {7}.
Area
The area (A) of a regular heptagon of side length a is given by:
This can be seen by subdividing the unit-sided heptagon into seven triangular "pie slices" with vertices at the center and at the heptagon's vertices, and then halving each triangle using the apothem as the common side. The apothem is half the cotangent of and the area of each of the 14 small triangles is one-fourth of the apothem.
The exact algebraic expression, starting from the cubic polynomial x3 + x2 − 2x − 1 (one of whose roots is )[1] is given in complex numbers by:
in which the imaginary parts offset each other leaving a real-valued expression. This expression cannot be algebraically rewritten without complex components, since the indicated cubic function is casus irreducibilis.
The area of a regular heptagon inscribed in a circle of radius R is while the area of the circle itself is thus the regular heptagon fills approximately 0.8710 of its circumscribed circle.
الإنشاء
As 7 is a Pierpont prime but not a Fermat prime, the regular heptagon is not constructible with compass and straightedge but is constructible with a marked ruler and compass. It is the smallest regular polygon with this property. This type of construction is called a neusis construction. It is also constructible with compass, straightedge and angle trisector. The impossibility of straightedge and compass construction follows from the observation that is a zero of the irreducible cubic x3 + x2 − 2x − 1. Consequently, this polynomial is the minimal polynomial of 2cos(2π⁄7), whereas the degree of the minimal polynomial for a constructible number must be a power of 2.
 A neusis construction of the interior angle in a regular heptagon. |
 An animation from a neusis construction with radius of circumcircle , according to Andrew M. Gleason[1] based on the angle trisection by means of the Tomahawk, pause at the end of 30 s. |
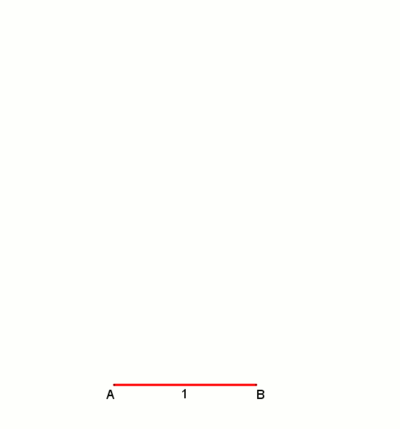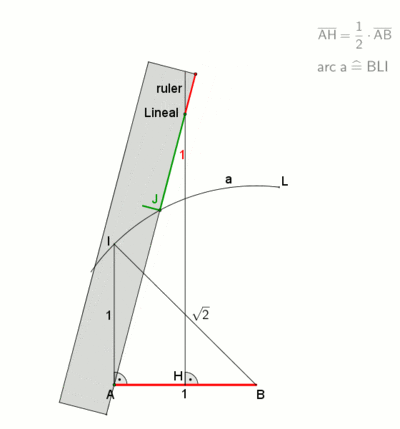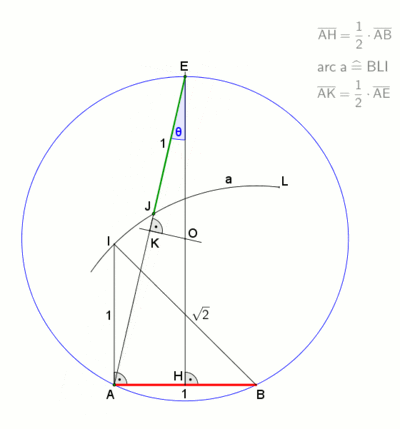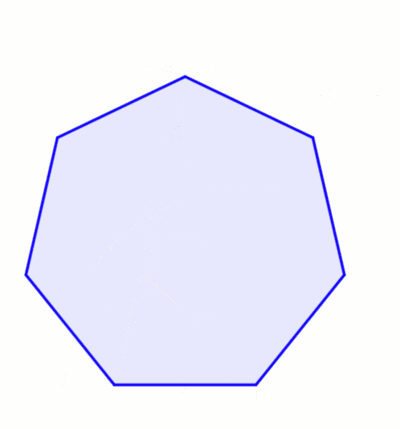
An animation from a neusis construction with marked ruler, according to David Johnson Leisk (Crockett Johnson),[2] pause at the end of 30 s.
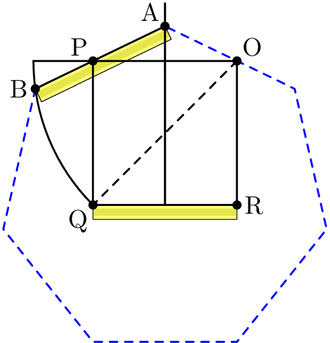
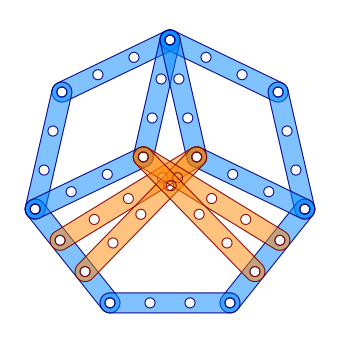
Gerard 't Hooft shows a regular heptagon made of only 15 strips of Meccano with bars sizes 8 and 11.[3]
The construction includes two isosceles triangles which hold the rest of bars fixed. The regular heptagon's side a, the shorter isosceles triangle side e, and the longer isosceles triangle side d satisfy
The formula is derived from this Heptagonal triangle formula:
Small possible heptagons constructions:
| Heptagon | a | d | e |
|---|---|---|---|
| 1 | 3 | 4 | 1 |
| 2 | 8 | 11 | 6 |
| 3 | 33 | 46 | 29 |
| 4 | 40 | 53 | 6 |
| 5 | 55 | 74 | 27 |
The smallest meccano heptagon 1:
Approximation
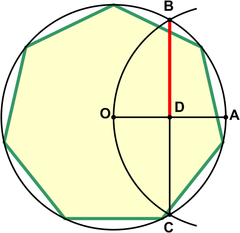
An approximation for practical use with an error of about 0.2% is shown in the drawing. It is attributed to Albrecht Dürer.[4] Let A lie on the circumference of the circumcircle. Draw arc BOC. Then gives an approximation for the edge of the heptagon.
This approximation uses for the side of the heptagon inscribed in the unit circle while the exact value is .
Example to illustrate the error:
At a circumscribed circle radius r = 1 m, the absolute error of the 1st side would be approximately -1.7 mm
A meccano approximation construction can be made with eleven bars of sizes 20, 36 and 45. These values leave an error around 0.1%.
Symmetry

Diagonals and heptagonal triangle
The regular heptagon's side a, shorter diagonal b, and longer diagonal c, with a<b<c, satisfy[6]
- (the optic equation)
and hence
and[6]
Thus –b/c, c/a, and a/b all satisfy the cubic equation However, no algebraic expressions with purely real terms exist for the solutions of this equation, because it is an example of casus irreducibilis.
The approximate lengths of the diagonals in terms of the side of the regular heptagon are given by
We also have[7]
and
A heptagonal triangle has vertices coinciding with the first, second, and fourth vertices of a regular heptagon (from an arbitrary starting vertex) and angles and Thus its sides coincide with one side and two particular diagonals of the regular heptagon.[6]
Star heptagons
Two kinds of star heptagons (heptagrams) can be constructed from regular heptagons, labeled by Schläfli symbols {7/2}, and {7/3}, with the divisor being the interval of connection.

Blue, {7/2} and green {7/3} star heptagons inside a red heptagon.
Empirical examples

Graphs
The K7 complete graph is often drawn as a regular heptagon with all 21 edges connected. This graph also represents an orthographic projection of the 7 vertices and 21 edges of the 6-simplex. The regular skew polygon around the perimeter is called the petrie polygon.
 6-simplex (6D) |
Heptagon in nature
See also
References
- ^ أ ب Gleason, Andrew Mattei (March 1988). "Angle trisection, the heptagon, and the triskaidecagon p. 186 (Fig.1) –187" (PDF). The American Mathematical Monthly. 95 (3): 185–194. doi:10.2307/2323624. Archived from the original (PDF) on 2015-12-19.
- ^ Weisstein, Eric W. "Heptagon." From MathWorld, A Wolfram Web Resource.
- ^ Gerard ’t Hooft. "Meccano Mathematics I"
- ^ G.H. Hughes, "The Polygons of Albrecht Dürer-1525, The Regular Heptagon", Fig. 11 the side of the Heptagon (7) Fig. 15, image on the left side, retrieved on 4 December 2015
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
- ^ أ ب ت Abdilkadir Altintas, "Some Collinearities in the Heptagonal Triangle", Forum Geometricorum 16, 2016, 249–256.http://forumgeom.fau.edu/FG2016volume16/FG201630.pdf
- ^ Leon Bankoff and Jack Garfunkel, "The heptagonal triangle", Mathematics Magazine 46 (1), January 1973, 7–19.
وصلات خارجية
- Definition and properties of a heptagon With interactive animation
- Heptagon according Johnson
- Another approximate construction method
- Polygons – Heptagons
- Recently discovered and highly accurate approximation for the construction of a regular heptagon.
- Heptagon, an approximating construction as an animation
- A heptagon with a given side, an approximating construction as an animation



![{\displaystyle A={\frac {a^{2}}{4}}{\sqrt {{\frac {7}{3}}\left(35+2{\sqrt[{3}]{14^{2}(13-3{\sqrt {-3}})}}+2{\sqrt[{3}]{14^{2}(13+3{\sqrt {-3}})}}\right)}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fd82d05bfd4b133f82db90486386b2ba458f5c4)