التفاضل والتكامل
| الحسبان |
|---|
حساب التفاضل والتكامل (باللاتينية: Calculus) فرع من فروع الرياضيات يدرس النهايات والاشتقاق والتكامل والمتسلسلات اللانهائية، وهو علم يستخدم لدراسة التغير في الدوال وتحليلها.
ويدخل علم التفاضل والتكامل في العديد من التطبيقات في الهندسة والعلوم المختلفة حيث كثيراً ما يحتاج لدراسة سلوك الدالة والتغير فيها وحل المشاكل التي يعجز علم الجبر عن حلها بسهولة،وعادة مايدرس علم التفاضل والتكامل بعد دراسة أساسيات الجبر والهندسة وحساب المثلثات، ومن الموضوعات الرئيسية في هذا العلم هي النهايات والكميات الموحلة في الصغر.
وينقسم إلى هذا العلم إلى فرعين هما التفاضل والتكامل ويربط بينهما ما يعرف بالنظرية الأساسية للتفاضل والتكامل. وفى بعض الأحيان قد يستخدم الاسم تفاضل وتكامل في الإشارة إلى أي نظام يستخدم في الحسبان ويستخدم فيه الرموز في التعامل مع المصطلحات والمتغيرات المختلفة مثل تفاضل وتكامل لامبدا والتفاضل والتكامل الاقتراحي والتفاضل والتكامل العلائقي والتفاضل والتكامل المؤكد.
التاريخ

التفاضل والتكامل ويطلق عليه أحيانا علم الحسبان. ومع أن اصول حسابِ التكامل تَعتبرُ قديمة جدا إلى ما قبل ظهورها في لغة يُونانِيَّة قدِيمَة، فهناك دليل أن المصريون القدماء لَرُبَما كانوا على علم بمثل هذه المعرفةِ أيضاً. (انظر ورق بردي موسكو الرياضي. ) يعتبر مع طريقة ، التي جَعلَت من الممكن حِساب المساحات وحجومِ المناطقِ والمواد الصلبةِ. طوّرَ أرخميدس هذه الطريقةِ أبعد من ذلك ، كما اخترع طرقا أيضاً التي تَشْبهُ المفاهيمَ المعاصرةَ.
عالم رياضيات هندي، باسكارا (1114-1185)، أعطىَ مثالَ على ما يدعى الآن "معامل تفاضلي" والفكرة الأساسية التي تعرف الآن بنظرية رول ". في القرن الرابع عشر قام عالم رياضيات هندي مادافا سويّة مع علماءِ الرياضيات الآخرينِ مدرسة كيرالا بانشاء طرق رئيسيةَ ادت إلى حساب التفاضل والتكاملِ الذي لَمْ يظهر من جديد في أي مكان في العالم حتى القرن السابع عشرِ مِن قِبل نيوتن ولايبتز. لايبنتز و نيوتن هما مخترعي حساب التفاضل والتكاملِ ، بشكل رئيسي لإكتشافاتِهم المنفصلةِ للنظريةِ الأساسيةِ لحساب التفاضل والتكاملِ والعملِ على الترقيمِ.
لقد كَانَ هناك نِقاشُ كبيرُ حول اسهام نيوتن أَو لايبنتز في أولوية اكتشاف المفاهيمِ المهمةِ لحساب التفاضل والتكاملِ.
الإسهام الثاني لتطويرِ حساب التفاضل والتكاملِ ييعزى إلى باروو، ديكارت، دي فيرما، هايغنس، و والس. اضافة لعالم رياضيات ياباني، كوا سيكي، الذي عاشَ في نفس الوقت مع لايبنتز ونيوتن وأسهبَ في بعض المبادئِ الأساسيةِ أيضاً مِنْ حسابِ التكامل، مع ذلك هذا لَمْ يُعْرَفُ في الغربِ في ذلك الوقت، ولم يكن لذيه عِنْدَهُ إتصالُ مَع العلماءِ الغربيينِ.
النهايات
 مقالة مفصلة: نهاية رياضية
مقالة مفصلة: نهاية رياضية
تهتم بدراسة اتصال الدالة وقيمتها عندما يقترب تابعها من قيمة معينة.
بفرض أن الدالة هي دالة حقيقية وأن عدد حقيقي أيضا:
عندئذ يمكن القول:
أي أن الدالة تكون قريبة جدا حسبما نريد من عندما تقترب من العدد ونعبر عن ذلك لغة (أن نهاية , عندما تؤول إلى , هي ).
التفاضل والاشتقاق
يَقِيسُ الإشتقاقُ حسّاسيةَ متغيّرِ تابع ( دالة ) بالنسبة إلى التغير في المتغيّرِ المستقل. أي تلميح الصيغةُ:
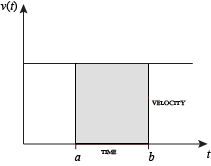
سرعته (إشتقاق الموضع بالنسبة للزمن) في سيارة تَصِفُ التغيرَ في الموقعِ نسبة إلى التغيرَ بمرور الزمن. يجب أن نتذكر أيضا أن السرعة نفسها قَدْ تَتغيّرُ في حالة الحركات المتسارعة ؛ يَتعاملُ حساب التفاضل والتكاملُ مع هذه الحالةِ الأكثر تعقيداً لكن الطبيعيةِ والمألوفةِ.
يُقرّرُ حسابُ التفاضل سرعة آنية ، بأي معيّنة مُعطية لحظة بمرور الوقت، ليس فقط سرعة متوسطة أثناء فترة مِنْ الوقتِ. سرعة الصيغةَ = مسافة / قدّمَ وقتُ إلى a لحظة وحيدة خارجُ القسمة بلا معنى "صفر منقسمة بحلول الصفر ". هذا مُتَجَنّبُ، على أية حال، لأن مسافةَ خارجَ القسمة / وقت لَمْ يُستَعملْ لa لحظة وحيدة (كما في a ما زالَتْ صورة)، لكن لفتراتِ الوقتِ الذي قصيرة جداً.
يُجيبُ الإشتقاقُ على السؤالِ: عندما يقارب الفترة الزمنية الصفر فما هي قيمة السرعة الوسطية المحسوبة عندئذ ؟ .
بشكل رسمي أكثر، يُعرّفُ حسابَ تفاضل النسبةَ الآنيةَ للتغيرِ ( إشتقاق ) من اجل دالة رياضية ل قيمة، إلى تغير المتغير المستقل لهذه الدالة.
إشتقاق دالة يَعطي معلومات حول القِطَعِ الصغيرةِ مِنْ مخططها البياني. فهو على علاقةُ مباشرة بإيجاد حدود عليا وحدود دنيا لدالة ؛ لأن في تلك النقاطِ يكون الرسم البياني معدوم التغير (وبمعنى آخر: إنّ ميل الرسم البياني في تلك النقاط صفر). التطبيق الآخر لحسابِ التفاضل هي طريقة نيوتن، وهي خوارزمية لإيجاد جذور دالة رياضية بتَقريب الدالة مِن قِبل مماساتها .
يتم اشتقاق التفاضل للدالة من التعريف الرئيسي للنهاية بالعلاقة:
- مشتفة الثابت :
عندما a هو عدد ثابت اذن
- مشتفة الدوال الاسية:
اذا كان r عدد حقيقي اذن:
مثال على ذلك: ,
- مشتفةالدوال الأسيه واللوغاريتمية :
- مشتقة دوال المثلثات العكسية:
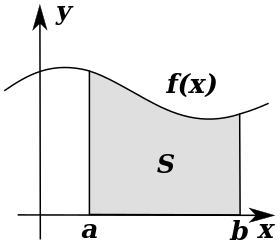
التكامل
في علم الرياضيات ينقسم التكامل إلى جزئين: التكامل المحدود والتكامل الغير محدود. يتعلق التكامل المحدود بحساب الأطوال, المساحات, المنحنيات, مراكز الثقل وما إلى ذلك من الدوال التي لها تطبيقات في شتى العلوم. من جهة أخرى يركز التكامل الغير محدود على إيجاد المعكوس الرياضي للتفاضل ولهذا السبب يسمى أيضا بالاشتقاق العكسي.
الاشتقاق العكسي
 مقالة مفصلة: اشتقاق عكسي
مقالة مفصلة: اشتقاق عكسي
يعطى التكامل الغير محدود لتابع رياضي بالعلاقة:
- حيث
التكامل المحدود
 مقالة مفصلة: تكامل محدود
مقالة مفصلة: تكامل محدود
يعبر عنه بالشكل الرياضي:
تطبيقات

لعلم التفاضل والتكامل تطبيقات لا حصر لها في علوم الفيزياء الكلاسيكية والحديثة, الكيمياء, الهندسة, الاقتصاد, الحاسوب وحتى في الطب وبعض العلوم السياسية والادبية. هنا بعض الامثلة:
- حساب اطوال المنحنيات, المساحات, والحجوم.
- حساب مركز الثقل, عزم القصور الذاتي, كمية التحرك, العجلة, السرعة, الإزاحة, الشغل, الطاقة.
- حساب التوزيعات والاحتمالات المنتظمة كاحتمالية فيرمي في أشباه الموصلات, انتشار جراثيم في وسط معين تحت ظروف بيئية معينة.
- حل المعادلات التفاضلية وتطبيقاتها في الأنظمة الخطية مثل البندول, دوائر الرنين الكهربائية, وأنظمة التحكم الكهروميكانيكية.
- اشتقاق الكثير من المعادلات الفيزيائية الحديثة والتي يكون من الصعب اجرائها تجريبيا.
- حساب الثوابت الرياضية إلى درجات عالية من الدقة مثل قيمة ثابت الدائرة ، الثابت الطبيعي وكذلك الدوال الرياضية المعقدة وإمكانية برمجة هذه العمليات بواسطة الحاسوب.
انظر أيضاً
قوائم
- قائمة موضوعات التفاضل والتكامل
- List of derivatives and integrals in alternative calculi
- List of differentiation identities
- قائمة منشورات التفاضل والتكامل
- Table of integrals
موضوعات أخرى متعلقة
- Calculus of finite differences
- Calculus with polynomials
- Complex analysis
- Differential equation
- Differential geometry
- Elementary Calculus: An Infinitesimal Approach
- Fourier series
- Integral equation
- Mathematical analysis
- Multivariable calculus
- Non-classical analysis
- Non-standard analysis
- Non-standard calculus
- Precalculus (التعليم الرياضيات)
- Product integral
- Stochastic calculus
- Taylor series
المصادر
الهوامش
كتب
- Larson, Ron, Bruce H. Edwards (2010). Calculus, 9th ed., Brooks Cole Cengage Learning. ISBN 978-0-547-16702-2
- McQuarrie, Donald A. (2003). Mathematical Methods for Scientists and Engineers, University Science Books. ISBN 978-1-891389-24-5
- Salas, Saturnino L.; Hille, Einar; Etgen, Garret J. (2006). Calculus: One and Several Variables (10th ed.). Wiley. ISBN 978-0-471-69804-3.
{{cite book}}: CS1 maint: location missing publisher (link) - Stewart, James (2008). Calculus: Early Transcendentals, 6th ed., Brooks Cole Cengage Learning. ISBN 978-0-495-01166-8
- Thomas, George B., Maurice D. Weir, Joel Hass, Frank R. Giordano (2008), Calculus, 11th ed., Addison-Wesley. ISBN 0-321-48987-X
مصادر أخرى
قراءات إضافية
- Boyer, Carl Benjamin (1949). The History of the Calculus and its Conceptual Development. Hafner. Dover edition 1959, ISBN 0-486-60509-4
- Courant, Richard ISBN 978-3-540-65058-4 Introduction to calculus and analysis 1.
- Edmund Landau. ISBN 0-8218-2830-4 Differential and Integral Calculus, American Mathematical Society.
- Robert A. Adams. (1999). ISBN 978-0-201-39607-2 Calculus: A complete course.
- Albers, Donald J.; Richard D. Anderson and Don O. Loftsgaarden, ed. (1986) Undergraduate Programs in the Mathematics and Computer Sciences: The 1985-1986 Survey, Mathematical Association of America No. 7.
- John Lane Bell: A Primer of Infinitesimal Analysis, Cambridge University Press, 1998. ISBN 978-0-521-62401-5. Uses synthetic differential geometry and nilpotent infinitesimals.
- Florian Cajori, "The History of Notations of the Calculus." Annals of Mathematics, 2nd Ser., Vol. 25, No. 1 (Sep., 1923), pp. 1–46.
- Leonid P. Lebedev and Michael J. Cloud: "Approximating Perfection: a Mathematician's Journey into the World of Mechanics, Ch. 1: The Tools of Calculus", Princeton Univ. Press, 2004.
- Cliff Pickover. (2003). ISBN 978-0-471-26987-8 Calculus and Pizza: A Math Cookbook for the Hungry Mind.
- Michael Spivak. (September 1994). ISBN 978-0-914098-89-8 Calculus. Publish or Perish publishing.
- Tom M. Apostol. (1967). ISBN 978-0-471-00005-1 Calculus, Volume 1, One-Variable Calculus with an Introduction to Linear Algebra. Wiley.
- Tom M. Apostol. (1969). ISBN 978-0-471-00007-5 Calculus, Volume 2, Multi-Variable Calculus and Linear Algebra with Applications. Wiley.
- Silvanus P. Thompson and Martin Gardner. (1998). ISBN 978-0-312-18548-0 Calculus Made Easy.
- Mathematical Association of America. (1988). Calculus for a New Century; A Pump, Not a Filter, The Association, Stony Brook, NY. ED 300 252.
- Thomas/Finney. (1996). ISBN 978-0-201-53174-9 Calculus and Analytic geometry 9th, Addison Wesley.
- Weisstein, Eric W. "Second Fundamental Theorem of Calculus." From MathWorld—A Wolfram Web Resource.
- Howard Anton,Irl Bivens,Stephen Davis:"Calculus",John Willey and Sons Pte. Ltd.,2002.ISBN 978-81-265-1259-1
كتب أونلاين
- Boelkins, M. (2012). "Active Calculus: a free, open text". Retrieved 1 Feb 2013 from http://gvsu.edu/s/km
- Crowell, B. (2003). "Calculus" Light and Matter, Fullerton. Retrieved 6 May 2007 from http://www.lightandmatter.com/calc/calc.pdf
- Garrett, P. (2006). "Notes on first year calculus" University of Minnesota. Retrieved 6 May 2007 from http://www.math.umn.edu/~garrett/calculus/first_year/notes.pdf
- Faraz, H. (2006). "Understanding Calculus" Retrieved 6 May 2007 from Understanding Calculus, URL http://www.understandingcalculus.com/ (HTML only)
- Keisler, H. J. (2000). "Elementary Calculus: An Approach Using Infinitesimals" Retrieved 29 August 2010 from http://www.math.wisc.edu/~keisler/calc.html
- Mauch, S. (2004). "Sean's Applied Math Book" California Institute of Technology. Retrieved 6 May 2007 from http://www.cacr.caltech.edu/~sean/applied_math.pdf
- Sloughter, Dan (2000). "Difference Equations to Differential Equations: An introduction to calculus". Retrieved 17 March 2009 from http://synechism.org/drupal/de2de/
- Stroyan, K.D. (2004). "A brief introduction to infinitesimal calculus" University of Iowa. Retrieved 6 May 2007 from http://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm (HTML only)
- Strang, G. (1991). "Calculus" Massachusetts Institute of Technology. Retrieved 6 May 2007 from http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm
- Smith, William V. (2001). "The Calculus" Retrieved 4 July 2008 [1] (HTML only).
وصلات خارجية
- Eric W. Weisstein, Calculus at MathWorld.
- قالب:PlanetMath
- Calculus Made Easy (1914) by Silvanus P. Thompson Full text in PDF
- Calculus on In Our Time at the BBC. (listen now)
- Calculus.org: The Calculus page at University of California, Davis – contains resources and links to other sites
- COW: Calculus on the Web at Temple University – contains resources ranging from pre-calculus and associated algebra
- Earliest Known Uses of Some of the Words of Mathematics: Calculus & Analysis
- Online Integrator (WebMathematica) from Wolfram Research
- The Role of Calculus in College Mathematics from ERICDigests.org
- OpenCourseWare Calculus from the Massachusetts Institute of Technology
- Infinitesimal Calculus – an article on its historical development, in Encyclopedia of Mathematics, ed. Michiel Hazewinkel.
- Calculus for Beginners and Artists by Daniel Kleitman, MIT
- Calculus Problems and Solutions by D. A. Kouba
- Donald Allen's notes on calculus
- Calculus training materials at imomath.com
- (إنگليزية) (بالعربية) The Excursion of Calculus, 1772