جبر ابتدائي
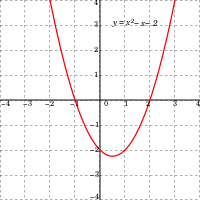
الجبر الابتدائي Elementary algebra هو أبسط أنواع الجبر وهو الذي يشكل الفرع الذي يتعامل مع كثيرات الحدود والمعادلات وطرق إيجاد جذور المعادلات وطرق حلها. It is often contrasted with arithmetic: arithmetic deals with specified numbers,[1] whilst algebra introduces variables (quantities without fixed values).[2]
This use of variables entails use of algebraic notation and an understanding of the general rules of the operations introduced in arithmetic. Unlike abstract algebra, elementary algebra is not concerned with algebraic structures outside the realm of real and complex numbers.
It is typically taught to secondary school students and builds on their understanding of arithmetic. The use of variables to denote quantities allows general relationships between quantities to be formally and concisely expressed, and thus enables solving a broader scope of problems. Many quantitative relationships in science and mathematics are expressed as algebraic equations.
الترميز الجبري
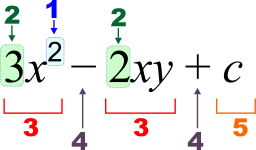
Algebraic notation describes the rules and conventions for writing mathematical expressions, as well as the terminology used for talking about parts of expressions. For example, the expression has the following components:
قوانين الجبر الابتدائي
- في التعابير الجبرية يتم اعتماد ترتيب العمليات كما يلي:
- مجموعات الأقواس -> الرفع إلى أس -> الضرب -> الجمع
- الجمع عملية تبديلية.
- مثال : اذا كان عندئذ
- الضرب عملية تبديلية أيضا.
- القسمة هي عكس عملية الضرب.
- يتم تحويل القسمة إلى ضرب بتحويل العدد المضروب به إلى مقلوب (رياضيات) :
- العملية الأسية ليس بعملية تبديلية .
- بعض العمليات الأسية لها عمليات معاكسة: لوغاريتم و العمليات الأسية ذات الأسس الكسرية (e.g. الجذر التربيعي).
- أمثلة: اذا عندئذ اذا عندئذ
- لا يوجد جذر تربيعي للأعداد السالبة ضمن مجموعة الأعداد الحقيقية
- بعض العمليات الأسية لها عمليات معاكسة: لوغاريتم و العمليات الأسية ذات الأسس الكسرية (e.g. الجذر التربيعي).
مجموعات الأعداد . (انظر : مجموعة الأعداد العقدية)
- Distributive property of exponentiation with respect to multiplication:
- ضرب العمليات الأسية :
- اذا و ، عندئذ (العلاقة المتعدية للمساواة).
- (العلاقة الإنعكاسية للمساواة).
- اذا كان عندئذ (تناظر المساواة ).
- اذا كان and عندئذ
- اذا كان عندئذ for أيا كانت c، نتيجة الخاصة الإنعكاسية للمساواة.
- اذا كانت و عندئذ =
- اذا كان عندئذ من أجل أي قيمة c نتيجة الخاصية الإنعكاسية للمساواة الجبرية.
- اذا تساوى رمزين جبريين فيمكن أن نستبدل أي منهما بالآخر عند ما نريد .
- اذا كان و عندئذ
(الخاصية المتعدية للمتراجحة (لا مساواة)).
- اذا كانت عندئذ
for أيا كانت c.
- اذا كان و عندئذ
- اذا كان و عندئذ
انظر أيضاً
- History of elementary algebra
- Binary operation
- Gaussian elimination
- Mathematics education
- Number line
- Polynomial
- Cancelling out
- Tarski's high school algebra problem
المراجع
- Leonhard Euler, Elements of Algebra, 1770. English translation Tarquin Press, 2007, ISBN 978-1-899618-79-8, also online digitized editions[3] 2006,[4] 1822.
- Charles Smith, A Treatise on Algebra, in Cornell University Library Historical Math Monographs.
- Redden, John. Elementary Algebra Archived 2016-06-10 at the Wayback Machine. Flat World Knowledge, 2011
- ^ H.E. Slaught and N.J. Lennes, Elementary algebra, Publ. Allyn and Bacon, 1915, page 1 (republished by Forgotten Books)
- ^ Lewis Hirsch, Arthur Goodman, Understanding Elementary Algebra With Geometry: A Course for College Students, Publisher: Cengage Learning, 2005, ISBN 0534999727, 9780534999728, 654 pages, page 2
- ^ Euler's Elements of Algebra Archived 2011-04-13 at the Wayback Machine
- ^ Euler, Leonhard; Hewlett, John; Horner, Francis; Bernoulli, Jean; Lagrange, Joseph Louis (4 May 2018). "Elements of Algebra". Longman, Orme. Retrieved 4 May 2018 – via Google Books.
وصلات خارجية
 Media related to جبر ابتدائي at Wikimedia Commons
Media related to جبر ابتدائي at Wikimedia Commons