شغل (فيزياء)
الشغل (أو العمل) ، في علم الفيزياء هو كمية الطاقة المتحولة للتحريك بقوة ما لمسافة ما.
Mathematical calculation
For moving objects, the quantity of work/time (power) is integrated along the trajectory of the point of application of the force. Thus, at any instant, the rate of the work done by a force (measured in joules/second, or watts) is the scalar product of the force (a vector), and the velocity vector of the point of application. This scalar product of force and velocity is known as instantaneous power. Just as velocities may be integrated over time to obtain a total distance, by the fundamental theorem of calculus, the total work along a path is similarly the time-integral of instantaneous power applied along the trajectory of the point of application.[1]
Work is the result of a force on a point that follows a curve X, with a velocity v, at each instant. The small amount of work δW that occurs over an instant of time dt is calculated as
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta W = \mathbf{F}\cdot d\mathbf{s} = \mathbf{F}\cdot\mathbf{v}dt }
where the F ⋅ v is the power over the instant dt. The sum of these small amounts of work over the trajectory of the point yields the work,
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = \int_{t_1}^{t_2}\mathbf{F} \cdot \mathbf{v}dt = \int_{t_1}^{t_2}\mathbf{F} \cdot {\tfrac{d\mathbf{s}}{dt}}dt =\int_C \mathbf{F} \cdot d\mathbf{s},}
where C is the trajectory from x(t1) to x(t2). This integral is computed along the trajectory of the particle, and is therefore said to be path dependent.
If the force is always directed along this line, and the magnitude of the force is F, then this integral simplifies to
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = \int_C F\,ds}
where s is displacement along the line. If F is constant, in addition to being directed along the line, then the integral simplifies further to
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = \int_C F\,ds = F\int_C ds = Fs}
where s is the displacement of the point along the line.
This calculation can be generalized for a constant force that is not directed along the line, followed by the particle. In this case the dot product F ⋅ ds = F cos θ ds, where θ is the angle between the force vector and the direction of movement,[1] that is
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = \int_C \mathbf{F} \cdot d\mathbf{s} = Fs\cos\theta.}
In the notable case of a force applied to a body always at an angle of 90° from the velocity vector (as when a body moves in a circle under a central force), no work is done at all, since the cosine of 90 degrees is zero. Thus, no work can be performed by gravity on a planet with a circular orbit (this is ideal, as all orbits are slightly elliptical). Also, no work is done on a body moving circularly at a constant speed while constrained by mechanical force, such as moving at constant speed in a frictionless ideal centrifuge.
Work done by a variable force
Calculating the work as "force times straight path segment" would only apply in the most simple of circumstances, as noted above. If force is changing, or if the body is moving along a curved path, possibly rotating and not necessarily rigid, then only the path of the application point of the force is relevant for the work done, and only the component of the force parallel to the application point velocity is doing work (positive work when in the same direction, and negative when in the opposite direction of the velocity). This component of force can be described by the scalar quantity called scalar tangential component (خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle F\cos\theta} , where خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \theta} is the angle between the force and the velocity). And then the most general definition of work can be formulated as follows:
- Work of a force is the line integral of its scalar tangential component along the path of its application point.
- If the force varies (e.g. compressing a spring) we need to use calculus to find the work done. If the force is given by F(x) (a function of x) then the work done by the force along the x-axis from خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} is:
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = \int\limits_{a}^{b} \mathbf{F(s)} \cdot d\mathbf{s}}
Torque and rotation
A force couple results from equal and opposite forces, acting on two different points of a rigid body. The sum (resultant) of these forces may cancel, but their effect on the body is the couple or torque T. The work of the torque is calculated as
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle dW = \mathbf{T}\cdot\vec{\omega}dt,}
where the T ⋅ ω is the power over the instant δt. The sum of these small amounts of work over the trajectory of the rigid body yields the work,
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = \int_{t_1}^{t_2}\mathbf{T}\cdot\vec{\omega}dt.}
This integral is computed along the trajectory of the rigid body with an angular velocity ω that varies with time, and is therefore said to be path dependent.
If the angular velocity vector maintains a constant direction, then it takes the form,
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{\omega}= \dot{\phi}\mathbf{S},}
where φ is the angle of rotation about the constant unit vector S. In this case, the work of the torque becomes,
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = \int_{t_1}^{t_2}\mathbf{T}\cdot\vec{\omega}dt = \int_{t_1}^{t_2}\mathbf{T}\cdot \mathbf{S}\frac{d\phi}{dt}dt = \int_C\mathbf{T}\cdot \mathbf{S} d\phi,}
where C is the trajectory from φ(t1) to φ(t2). This integral depends on the rotational trajectory φ(t), and is therefore path-dependent.
If the torque T is aligned with the angular velocity vector so that,
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{T}=\tau\mathbf{S},}
and both the torque and angular velocity are constant, then the work takes the form,[2]
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = \int_{t_1}^{t_2}\tau \dot{\phi}dt = \tau(\phi_2-\phi_1).}
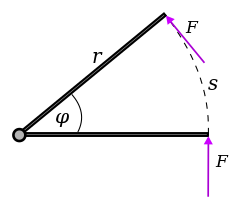
This result can be understood more simply by considering the torque as arising from a force of constant magnitude F, being applied perpendicularly to a lever arm at a distance r, as shown in the figure. This force will act through the distance along the circular arc s = rφ, so the work done is
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W=Fs = Fr\phi .}
Introduce the torque τ = Fr, to obtain
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W=Fr\phi=\tau\phi,}
as presented above.
Notice that only the component of torque in the direction of the angular velocity vector contributes to the work.
Work and potential energy
The scalar product of a force F and the velocity v of its point of application defines the power input to a system at an instant of time. Integration of this power over the trajectory of the point of application, C = x(t), defines the work input to the system by the force.
Path dependence
Therefore, the work done by a force F on an object that travels along a curve C is given by the line integral:
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = \int_C \mathbf{F} \cdot d\mathbf{x} = \int_{t_1}^{t_2}\mathbf{F}\cdot \mathbf{v}dt,}
where dx(t) defines the trajectory C and v is the velocity along this trajectory. In general this integral requires the path along which the velocity is defined, so the evaluation of work is said to be path dependent.
The time derivative of the integral for work yields the instantaneous power,
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dW}{dt} = P(t) = \mathbf{F}\cdot \mathbf{v} .}
Path independence
If the work for an applied force is independent of the path, then the work done by the force, by the gradient theorem, defines a potential function which is evaluated at the start and end of the trajectory of the point of application. This means that there is a potential function U(x), that can be evaluated at the two points x(t1) and x(t2) to obtain the work over any trajectory between these two points. It is tradition to define this function with a negative sign so that positive work is a reduction in the potential, that is
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W = \int_C \mathbf{F} \cdot \mathrm{d}\mathbf{x} = \int_{\mathbf{x}(t_1)}^{\mathbf{x}(t_2)} \mathbf{F} \cdot \mathrm{d}\mathbf{x} = U(\mathbf{x}(t_1))-U(\mathbf{x}(t_2)). }
The function U(x) is called the potential energy associated with the applied force. The force derived from such a potential function is said to be conservative. Examples of forces that have potential energies are gravity and spring forces.
In this case, the gradient of work yields
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla W = -\nabla U= -\left(\frac{\partial U}{\partial x}, \frac{\partial U}{\partial y}, \frac{\partial U}{\partial z}\right) = \mathbf{F},}
and the force F is said to be "derivable from a potential."[3]
Because the potential U defines a force F at every point x in space, the set of forces is called a force field. The power applied to a body by a force field is obtained from the gradient of the work, or potential, in the direction of the velocity V of the body, that is
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(t) = -\nabla U \cdot \mathbf{v} = \mathbf{F}\cdot\mathbf{v}.}
Work by a spring
Consider a spring that exerts a horizontal force F = (−kx, 0, 0) that is proportional to its deflection in the x direction independent of how a body moves. The work of this spring on a body moving along the space with the curve X(t) = (x(t), y(t), z(t)), is calculated using its velocity, v = (vx, vy, vz), to obtain
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W=\int_0^t\mathbf{F}\cdot\mathbf{v}dt =-\int_0^tkx v_x dt = -\frac{1}{2}kx^2. }
For convenience, consider contact with the spring occurs at t = 0, then the integral of the product of the distance x and the x-velocity, xvx, is (1/2)x2. The velocity is not a factor here. The work is the product of the distance times the spring force, which is also dependent on distance; hence the x2 result.
Work by a gas
- خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle W=\int_a^b{P}dV }
Where P is pressure, V is volume, and a and b are initial and final volumes.
مراجع
- ^ أ ب Resnick, Robert and Halliday, David (1966), Physics, Section 1–3 (Vol I and II, Combined edition), Wiley International Edition, Library of Congress Catalog Card No. 66-11527
- ^ Hugh D. Young; Roger A. Freedman (2008). University Physics (12th ed.). Addison-Wesley. p. 329. ISBN 978-0-321-50130-1.
{{cite book}}: Unknown parameter|lastauthoramp=ignored (|name-list-style=suggested) (help) - ^ J. R. Taylor, Classical Mechanics, University Science Books, 2005.