عدد برنولي
| n | الكسر | العشري |
|---|---|---|
| 0 | 1 | +1.000000000 |
| 1 | ±1/2 | ±0.500000000 |
| 2 | 1/6 | +0.166666666 |
| 3 | 0 | +0.000000000 |
| 4 | −1/30 | −0.033333333 |
| 5 | 0 | +0.000000000 |
| 6 | 1/42 | +0.023809523 |
| 7 | 0 | +0.000000000 |
| 8 | −1/30 | −0.033333333 |
| 9 | 0 | +0.000000000 |
| 10 | 5/66 | +0.075757575 |
| 11 | 0 | +0.000000000 |
| 12 | −691/2730 | −0.253113553 |
| 13 | 0 | +0.000000000 |
| 14 | 7/6 | +1.166666666 |
| 15 | 0 | +0.000000000 |
| 16 | −3617/510 | −7.092156862 |
| 17 | 0 | +0.000000000 |
| 18 | 43867/798 | +54.97117794 |
| 19 | 0 | +0.000000000 |
| 20 | −174611/330 | −529.1242424 |
في الرياضيات ، أعداد برنولي Bernoulli numbers ، هي متتالية من الأعداد الكسرية ذات علاقة وثيقة مع نظرية الأعداد، ويرتبطون بقيم اقتران ريمان الزائي للأرقام الصحيحة السالبة.
وفي اوروبا، كان أول من درس تلك الأعداد جاكوب برنولي، مما حدا بعالم الرياضيات ابراهام ده مواڤر، أن يسميهم "أعداد برنولي". وفي اليابان، ربما قبل اوروبا، فقد اكتشفهم سـِكي كـُوا. ويظهرون في فرد متسلسلة تايلور لدوال الظل (ظا) والظل الزائدي، في صيغة اويلر–مكلورين، وفي التعبيرات عن قيم معينة لاقتران ريمان الزائي.
وفي ملحوظة G في ملاحظات ادا لڤليس على الآلة التحليلية التي كتبتها سنة 1842، تصف لڤليس خوارزمية لتوليد أعداد برنولي بواسطة ماكينة بابدج [1]. ونتيجة لذلك، فأعداد برنولي نالهم شرف أنهم كانوا موضوع أول برنامج حاسوب.
مقدمة
أعداد برنولي Bn، أحياناً يـُرمز لها bn. تم اكتشافهم لأول مرة فيما يرتبط مع الأشكال المغلقة لعمليات الجمع
لمختلف القيم المحددة للمتغير n. الأشكال المغلقة هم دوماً متعددات حدود في m من الدرجة n + 1. معاملات عديدات الحدود تلك يرتبطن بدرجة وثيقة بأعداد برنولي، التي على صلة بصيغة فاولهابر:
فعلى سبيل المثال، لو أخذنا n لتساوي 1،
الدوال المولـِّدة
وبفردها كحاضل ضرب كوشي وإعادة ترتيب قليلاً، نحصل على
أشكال ورموز أخرى
فلكل m > 0، و B0 = 1.
قيم أعداد برنولي
Bn = 0 لكل قيم n الفردية عدا 1. B1 = 1/2 أو −1/2 حسب الاصطلاح المستخدم (انظر لاحقاً). أول بضعة أداد برنولي غير صفرية (المتتاليات OEIS: A027641 و OEIS: A027642 في OEIS) وبعض الأعداد الأكبر مذكورين أدناه.
| n | N | D | Bn = N / D |
| 0 | 1 | 1 | +1.00000000000 |
| 1 | -1 | 2 | -0.50000000000 |
| 2 | 1 | 6 | +0.16666666667 |
| 4 | -1 | 30 | -0.03333333333 |
| 6 | 1 | 42 | +0.02380952381 |
| 8 | -1 | 30 | -0.03333333333 |
| 10 | 5 | 66 | +0.07575757576 |
| 12 | -691 | 2730 | -0.25311355311 |
| 14 | 7 | 6 | +1.16666666667 |
| 16 | -3617 | 510 | -7.09215686275 |
| 18 | 43867 | 798 | +54.9711779448 |
الحساب الفعال لأعداد برنولي
في بعض التطبيقات، من المفيد أن تستطيع حساب أعداد برنولي B0 إلى Bp − 3 modulo p، حيث p هو a prime; for example to test whether Vandiver's conjecture holds for p, or even just to determine whether p is an irregular prime. It is not feasible to carry out such a computation using the above recursive formulae, since at least (a constant multiple of) p2 arithmetic operations would be required. Fortunately, faster methods have been developed (Buhler et al. 2001) which require only O(p (log p)2) operations (see big-O notation).
وصف ديڤد هارڤي (Harvey 2008) خوارزمية لحساب أعداد برنولي بحساب Bn modulo p for للعديد من الأعداد الأولية الصغيرة p, ثم يعيد بناء Bn باستخدام Chinese Remainder Theorem. Harvey writes that the asymptotic time complexity of this algorithm is O(n2 log(n)2+eps) and claims that this implementation is significantly faster than implementations based on other methods. Harvey's implementation is included in Sage since version 3.1. Using this implementation Harvey computed Bn for n = 108, which is a new record (October 2008). Prior to that Bernd Kellner (Kellner 2002) computed Bn to full precision for n = 106 on December 2002 واُلكسندر پاڤليك (Pavlyk 2008) for n = 107 with 'Mathematica' on April 2008.
| الحاسب | السنة | n | الأرقام |
| ي. برنولي | ~1689 | 10 | 1 |
| ل. اويلر | 1748 | 30 | 8 |
| J.C. Adams | 1878 | 62 | 36 |
| د. إ. كنوث، ت.ج. بكهولتس | 1967 | 360 | 478 |
| G. Fee, S. Plouffe | 1996 | 10000 | 27677 |
| G. Fee, S. Plouffe | 1996 | 100000 | 376755 |
| B.C. Kellner | 2002 | 1000000 | 4767529 |
| اُلكسندر پاڤليك | 2008 | 10000000 | 57675260 |
| د. هارڤي | 2008 | 100000000 | 676752569 |
إعادة بناء 'Summae Potestatum'
| ياكوب برنولي: Summae Potestatum، سنة 1713 |
وجهات نظر مختلفة
-
أرقام برنولى هى كيان رياضى قائم بذاته .
إرتباط تسلسلى: 1/6, −1/30, 1/42, −1/30,...
هذه هي وجهة نظر ياكوب بيرنولي. (أنظر الى النبذة من Ars Conjectandi, الطبعة الأولى, 1713). أعداد برنولي تفهم كأرقام , تكرارية في طبيعتها,أبتكرت لحل مسائل أو معضلات رياضية معينة, جمع الأسس (الجمع من أس), الذى يعنىparadigmatic application لبرنولي. أنه لمضلل أن نسمى وحهة النظر تلك 'قديمة'. فمثلا چين -بيير سيريه ويستخدم في تقريره الكتاب الرائع فصل في دراسة الرياضيات وهو من الكتب الأساسية المستخدمة في كثير من الجامعات اليوم . -
أعداد بيرنولي أشياء تجميعية .
تسلسل إرتباطى: 1, +1/2, 1/6, 0,....
هذا الرأي ، ويركز على العلاقة بين ستيرلنغ وأرقام وأعداد بيرنولي من الطبيعي أن تنشأ في حساب التفاضل والتكامل المحدد الإختلافات. في أكثر صوره عمومية و إدماجا من تلك العلاقة نلخصها بالتعريف أن ستيرلنج عديدة الحدود σn(x), formula (6.52) في Concrete Mathematics by Graham, Knuth and Patashnik. -
Bernoulli numbers as values of a sequence of certain polynomials.
Assuming the Bernoulli polynomials as already introduced the Bernoulli numbers can be defined in two different ways:
Bn = Bn(0). Associated sequence: 1, −1/2, 1/6, 0,....
Bn = Bn(1). Associated sequence: 1, +1/2, 1/6, 0,....
The two definitions differ only in the sign of B1. The choice Bn = Bn(0) is the convention used in the Handbook of Mathematical Functions. -
Bernoulli numbers as values of the Riemann zeta function.
Associated sequence: 1, +1/2, 1/6, 0,....
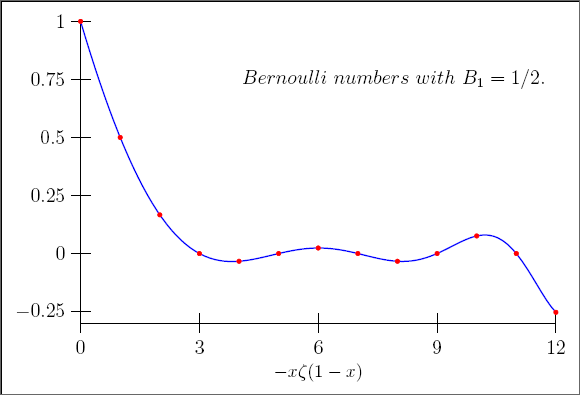
This convention agrees with the convention Bn = Bn(1) (for example J. Neukirch and M. Kaneko). The sign '+' for B1 matches the representation of the Bernoulli numbers by the Riemann zeta function. In fact the identity nζ(1−n) = (−1)n+1Bn valid for all n > 0 is then replaced by the simpler nζ(1−n) = -Bn. (See the paper of S. C. Woon.)
(Note that in the foregoing equation for n = 0 and n = 1 the expression −nζ(1 − n) is to be understood as limx → n −xζ(1 − x).)
تطبيقات أعداد برنولي
Arguably the most important application of the Bernoulli number in mathematics is their use in the Euler-MacLaurin formula. Assuming that f is a sufficiently often differentiable function the Euler-MacLaurin formula can be written as [~ 1]
This formulation assumes the convention B1 = -1/2. However, if one sets B1 = 1/2 then this formula can also be written as
Here f(0) = f which is a commonly used notation identifying the zero-th derivative of f with f. Moreover, let f(-1) denote an antiderivative of f. By the fundamental theorem of calculus . Thus the last formula can be further simplified to the following succinct form of the Euler-Maclaurin formula
This form is for example the source for the important Euler-MacLaurin expansion of the zeta function
Here denotes the rising factorial power.[~ 2]
تعاريف إندماجية
Connection with the Worpitzky number
A Bernoulli number is then introduced as an inclusion-exclusion sum of Worpitzky numbers weighted by the sequence 1, 1/2, 1/3,...
| Worpitzky's representation of the Bernoulli number | ||
| B0 | = | 1/1 |
| B1 | = | 1/1 − 1/2 |
| B2 | = | 1/1 − 3/2 + 2/3 |
| B3 | = | 1/1 − 7/2 + 12/3 − 6/4 |
| B4 | = | 1/1 − 15/2 + 50/3 − 60/4 + 24/5 |
| B5 | = | 1/1 − 31/2 + 180/3 − 390/4 + 360/5 − 120/6 |
| B6 | = | 1/1 − 63/2 + 602/3 − 2100/4 + 3360/5 − 2520/6 + 720/7 |
This representation has B1 = 1/2.
العلاقة بعدد فئة سترلنگ
A similar combinatorial representation derives from
العلاقة بعدد دورة سترلنگ
Let denote the signless Stirling cycle number. The two main formulas relating these number to the Bernoulli number (B1 = 1/2) are
and the inversion of this sum (for n ≥ 0, m ≥ 0)
Here the number An,m are the rational Akiyama-Tanigawa number, the first few of which are displayed in the following table.
| Akiyama-Tanigawa number | |||||
| n \ m | 0 | 1 | 2 | 3 | 4 |
| 0 | 1 | 1/2 | 1/3 | 1/4 | 1/5 |
| 1 | 1/2 | 1/3 | 1/4 | 1/5 | ... |
| 2 | 1/6 | 1/6 | 3/20 | ... | ... |
| 3 | 0 | 1/30 | ... | ... | ... |
| 4 | -1/30 | ... | ... | ... | ... |
These relations lead to a simple algorithm to compute the Bernoulli number. The input is the first row, A0,m = 1/(m + 1) and the output are the Bernoulli number in the first column An,0 = Bn . This transformation is shown in pseudo-code below.
| Akiyama-Tanigawa algorithm for Bn | ||||||||
| Enter integer n. For m from 0 by 1 to n do
|
العلاقة بعدد اويلر
Both formulas are valid for n ≥ 0 if B1 is set to 1/2. If B1 is set to −1/2 they are valid only for n ≥ 1 and n ≥ 2 respectively.
تقريب مقارب
It then follows from the Stirling formula that, as n goes to infinity,
Integral representation and continuation
The integral
has as special values b(2n) = B2n for n > 0. The integral might be considered as a continuation of the Bernoulli numbers to the complex plane and this was indeed suggested by Peter Luschny in 2004.[بحاجة لمصدر]
For example b(3) = (3/2)ζ(3)Π−3Ι and b(5) = −(15/2) ζ(5) Π −5Ι. Here ζ(n) denotes the Riemann zeta function and Ι the imaginary unit. It is remarkable that already Leonhard Euler (Opera Omnia, Ser. 1, Vol. 10, p. 351) considered these numbers and calculated
العلاقة بأعداد اويلر و ط π
The Euler numbers are a sequence of integers intimately connected with the Bernoulli numbers. Comparing the asymptotic expansions of the Bernoulli and the Euler numbers shows that the Euler numbers E2n are in magnitude approximately (2/π)(42n − 22n) times larger than the Bernoulli numbers B2n. In consequence:
This asymptotic equation reveals that π lies in the common root of both the Bernoulli and the Euler numbers. In fact π could be computed from these rational approximations.
Bernoulli numbers can be expressed through the Euler numbers and vice versa. Since for n odd Bn = En = 0 (with the exception B1), it suffices to regard the case when n is even.
These conversion formulas express an inverse relation between the Bernoulli and the Euler numbers. But more important, there is a deep arithmetic root common to both kinds of numbers, which can be expressed through a more fundamental sequence of numbers, also closely tied to π. These numbers are defined for n > 1 as
and S1 = 1 by convention. The magic of these numbers lies in the fact that they turn out to be rational numbers. This was first proved by Leonhard Euler 1734 in a landmark paper `De summis serierum reciprocarum' (On the sums of series of reciprocals) and fascinated mathematicians ever since. The first few of these numbers are
The Bernoulli numbers and Euler numbers are best understood as special views of these numbers, selected from the sequence Sn and scaled for use in special applications.
The expression [n even] has the value 1 if n is even and 0 otherwise (Iverson bracket).
These identities show that the quotient of Bernoulli and Euler numbers at the beginning of this section is just the special case of Rn = 2 Sn / Sn+1 when n is even. The Rn are rational approximations to π and two successive terms always enclose the true value of π. Beginning with n = 1 the sequence starts
These rational numbers also appear in the last paragraph of Euler's paper cited above. But it was only in September 2007 that this classical sequence found its way into the Encyclopedia of Integer Sequences (A132049).
نظرة خوارزمية: مثلث سايدل
The sequence Sn has another unexpected yet important property: The denominators of Sn divide the factorial (n − 1)!. In other words: the numbers Tn = Sn(n − 1)! are integers.
Thus the above representations of the Bernoulli and Euler numbers can be rewritten in terms of this sequence as
These identities make it easy to compute the Bernoulli and Euler numbers: the Euler numbers En are given immediately by T2n + 1 and the Bernoulli numbers B2n are obtained from T2n by some easy shifting, avoiding rational arithmetic.
What remains is to find a convenient way to compute the numbers Tn. However, already in 1877 Philipp Ludwig von Seidel published an ingenious algorithm which makes it extremely simple to calculate Tn.
| Seidel's algorithm for Tn |
نظرة توافيقية: تباديل متغايرة
 مقالة مفصلة: تباديل متغايرة
مقالة مفصلة: تباديل متغايرة
The coefficients are the Euler numbers of odd and even index, respectively. In consequence the ordinary expansion of tan x + sec x has as coefficients the rational numbers Sn.
تعميمات بعديدات الحدود
الخصائص الحسابية لأعداد برنولي
مبرهنة فون شتاوت-كلاوسن
| Clausen's algorithm for the denominator of Bn | ||
| Clausen: function(integer n) | | | n = 88 |
| S = divisors(n); | | | {1, 2, 4, 8, 11, 22, 44, 88} |
| S = map(k → k + 1, S); | | | {2, 3, 5, 9, 12, 23, 45, 89} |
| S = select(isprime, S); | | | {2, 3, 5, 23, 89} |
| return product(S); | | | 61410 |
| Von Staudt–Clausen representation of Bn | ||
| B0 | = | 1 |
| B1 | = | 1 − 1/2 |
| B2 | = | 1 − 1/2 − 1/3 |
| B4 | = | 1 − 1/2 − 1/3 − 1/5 |
| B6 | = | 1 − 1/2 − 1/3 − 1/7 |
| B8 | = | 1 − 1/2 − 1/3 − 1/5 |
| B10 | = | 1 − 1/2 − 1/3 − 1/11 |
The theorem affirms the existence of an integer In such that
The sum is over the primes p for which p − 1 divides n. These are the same primes which are employed in the Clausen algorithm. The proposition holds true for all n ≥ 0, not only for even n. I1 = 2 and for odd n > 1, In = 1.
Consequences of the von Staudt–Clausen theorem are: the denominators of the Bernoulli numbers are square-free and for n ≥ 2 divisible by 6.
لماذا تختفي أعداد برنولي الفردية؟
The sum
can be evaluated for negative values of the index n. Doing so will show that it is an odd function for even values of k, which implies that the sum has only terms of odd index. This and the formula for the Bernoulli sum imply that B2k+1−m is 0 for m odd and greater than 1; and that the term for B1 is cancelled by the subtraction. The von Staudt-Clausen theorem combined with Worpitzky's representation also gives a combinatorial answer to this question (valid for n > 1).
From the von Staudt-Clausen theorem it is known that for odd n > 1 the number 2Bn is an integer. This seems trivial if one knows beforehand that in this case Bn = 0. However, by applying Worpitzky's representation one gets
as a sum of integers, which is not trivial. Here a combinatorial fact comes to surface which explains the vanishing of the Bernoulli numbers at odd index. Let Sn,m be the number of surjective maps from {1, 2, ..., n} to {1, 2, ..., m}, then . The last equation can only hold if
This equation can be proved by induction. The first two examples of this equation are
n = 4 : 2 + 8 = 7 + 3, n = 6: 2 + 120 + 144 = 31 + 195 + 40.
Thus the Bernoulli numbers vanish at odd index because some non-obvious combinatorial identities are embodied in the Bernoulli numbers.
p-adic continuity
An especially important congruence property of the Bernoulli numbers can be characterized as a p-adic continuity property. If b, m and n are positive integers such that m and n are not divisible by p − 1 and , then
Since , this can also be written
where u = 1 − m and v = 1 − n, so that u and v are nonpositive and not congruent to 1 mod p − 1. This tells us that the Riemann zeta function, with 1 − p−s taken out of the Euler product formula, is continuous in the p-adic numbers on odd negative integers congruent mod p − 1 to a particular , and so can be extended to a continuous function for all p-adic integers the p-adic Zeta function.
أعداد برنولي وفرضية ريمان
For every ε > 1/4 there exists a constant Cε > 0 (depending on ε) such that |R(x)| < Cε xε as x → ∞. Here R(x) is the Riesz function
denotes the rising factorial power in the notation of D. E. Knuth. The number βn = Bn/n occur frequently in the study of the zeta function and are significant because βn is a p-integer for primes p where p − 1 does not divide n. The βn are called divided Bernoulli number.
Ramanujan's congruences
The following relations, due to Ramanujan, provide a more efficient method for calculating Bernoulli numbers:
استخدام أعداد برنولي في الطوبولجيا
The Kervaire-Milnor formula for the order of the cyclic group of diffeomorphism classes of exotic (4n − 1)-spheres which bound parallelizable manifolds for involves Bernoulli numbers; if B(n) is the numerator of B4n/n, then
is the number of such exotic spheres. (The formula in the topological literature differs because topologists use a different convention for naming Bernoulli numbers; this article uses the number theorists' convention.)
هويات متنوعة
-
Let n be non-negative and even
- The nth cumulant of the uniform probability distribution on the interval [−1, 0] is Bn/n.
-
Let n¡ = 1/n! and n ≥ 1.
Then Bn is n! times the
determinant of the following matrix.
Bn = 1
───
n¡2¡ 1¡ 0 0 0 ... 0 3¡ 2¡ 1¡ 0 0 ... 0 4¡ 3¡ 2¡ 1¡ 0 ... 0 ... ... ... ... ... ... ... (n − 2)¡ ... ... 3¡ 2¡ 1¡ 0 (n − 1)¡ (n − 2)¡ ... ... 3¡ 2¡ 1¡ n¡ (n − 1)¡ (n − 2)¡ ... ... 3¡ 2¡ Thus the determinant is σn(1), the Stirling polynomial at x = 1.
-
Let n ≥ 1.
-
Let n ≥ 1. Then (von Ettingshausen 1827)
-
Let n ≥ 1 and m ≥ 1. Then (Carlitz 1968)
-
Let n ≥ 4 and
-
Let n ≥ 4. Yuri Matiyasevich found (1997)
-
Let n ≥ 1
-
The next formula is true for n ≥ 0 if B1 = B1(1) = 1/2, but only for n ≥ 1 if B1 = B1(0) = -1/2.
-
Let n ≥ 0 and [b] = 1 if b is true, 0 otherwise.
فك لغز أرقام برنولي
استطاع محمد التميمي 16 سنة ، وهو فتى عراقي يعيش في سويسرا منذ ستة أعوام، وفي غضون أربعة أشهر فقط وضع صيغة لتفنسير وتبسيط أرقام برنولي. ولم يقتنع معلمي التميمي في البداية بعمله، مما دعاه إلى الاتصال بأساتذة فيجامعة ابسالا، وهي إحدى أعرق الجامعات السويدية ليطلب منهم التدقيق في عمله.وأضافت الوكالة أن الأساتذة وجدوا أن حله صحيح وعرضوا عليه الانضمام إلى جامعة ابسالا. التميمي أشار إلى أنه يريد التركيز حاليا على دراسته المدرسية وينوي تلقي دروس مكثفة في الرياضيات والفيزياء خلال الصيف، لافتا إلى رغبته في أن يكون باحثا في الفيزياء أو الرياضيات. [2]
انظر أيضا
- برنولي
- poly-Bernoulli number
- q-Bernoulli number
- Bernoulli polynomials
- Riemann zeta function
- Hurwitz zeta function
- Euler number
- Euler summation
- محمد التميمي
ملاحظات
المصادر
- Abramowitz, M.; Stegun, C. A. (1972), "§23.1: Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (9th printing ed.), New York: Dover, pp. 804–806.
- André, D. (1879), "Développements de sec x et tan x.", Comptes Rendus Acad. Sci. 88: 965–967.
- André, D. (1881), "Mémoire sur les permutations alternées", J. Math. 7: 167–184.
- Arlettaz, D. (1998), "Die Bernoulli-Zahlen: eine Beziehung zwischen Topologie und Gruppentheorie", Math. Semesterber 45: 61–75, doi:.
- Arnold, V. I. (1991), "Bernoulli-Euler updown numbers associated with function singularities, their combinatorics and arithmetics", Duke Math. J. 63: 537–555.
- Ayoub, A. (1981), "Euler and the Zeta Function", Amer. Math. Monthly 74: 1067–1086.
- Buhler, J.; Crandall, R.; Ernvall, R.; Metsankyla, T.; Shokrollahi, M. (2001), "Irregular Primes and Cyclotomic Invariants to 12 Million", Journal of Symbolic Computation'' 31 (1–2): 89–96, doi:.
- Carlitz, L. (1968), "Bernoulli Numbers.", Fib. Quart. 6: 71–85.
- Clausen, Thomas (1840), "Lehrsatz aus einer Abhandlung über die Bernoullischen Zahlen", Astr. Nachr. 17: 351–352.
- Conway, John; Guy (1996), The Book of Numbers, Springer-Verlag.
- Dumont, D.; Viennot, G. (1980), "A combinatorial interpretation of Seidel generation of Genocchi numbers", Ann. Discrete Math. 6: 77–87, doi:.
- Dumont, D. (1981), "Matrices d'Euler-Seidel", Séminaire Lotharingien de Combinatoire, http://emis.u-strasbg.fr/journals/SLC/opapers/s05dumont.html
- Entringer, R. C. (1966), "A combinatorial interpretation of the Euler and Bernoulli numbers", Nieuw. Arch. V. Wiskunde 14: 241–6.
- von Ettingshausen, A. (1827), Vorlesungen über die höhere Mathematik, Bd. 1, Vienna: Carl Gerold.
- Euler, Leonhard (1735), "De summis serierum reciprocarum", Opera Omnia I.14, E 41,: 73–86; On the sums of series of reciprocals, arXiv:math/0506415v2 (math.HO).
- Fee, G.; Plouffe, S. (2007), An efficient algorithm for the computation of Bernoulli numbers. arXiv:math/0702300v2 (math.NT)
- Graham, R. L.; Knuth, D. E.; Patashnik, O. (1989), Concrete Mathematics, Addison-Wesley.
- Harvey, David (2008), A multimodular algorithm for computing Bernoulli numbers arXiv:0807.1347v2 math.NT
- Jordan, Charles (1950), Calculus of Finite Differences, New York: Chelsea Publ. Co..
- Kaneko, M. (2000), "The Akiyama-Tanigawa algorithm for Bernoulli numbers", Journal of Integer Sequences 12, http://www.cs.uwaterloo.ca/journals/JIS/vol3.html.
- Kellner, Bernd (2002), Program Calcbn - A program for calculating Bernoulli numbers, http://www.bernoulli.org/.
- Knuth, D. E.; Buckholtz, T. J. (1967), "Computation of Tangent, Euler, and Bernoulli Numbers", Mathematics of Computation 21: 663–688, doi:.
- Luschny, Peter (2007), An inclusion of the Bernoulli numbers, http://www.luschny.de/math/primes/bernincl.html
- Menabrea, L. F., "Sketch of the Analytic Engine invented by Charles Babbage, with notes upon the Memoir by the Translator Ada Augusta, Countess of Lovelace." Bibliothèque Universelle de Genève, October 1842, No. 82. http://www.fourmilab.ch/babbage/sketch.html
- Milnor, John W.; Stasheff, James D. (1974), "Appendix B: Bernoulli Numbers", Characteristic Classes, Annals of Mathematics Studies, 76, Princeton University Press and University of Tokyo Press, pp. 281–287.
- قالب:Neukirch ANT
- Pavlyk, Oleksandr (2008), Today We Broke the Bernoulli Record: From the Analytical Engine to Mathematica, Wolfram Blog, http://blog.wolfram.com/2008/04/29/today-we-broke-the-bernoulli-record-from-the-analytical-engine-to-mathematica/.
- Riesz, M. (1916), "Sur l'hypothèse de Riemann", Acta Mathematica 40: 185–90, doi:.
- Seidel, L. (1877), "Über eine einfache Entstehungsweise der Bernoullischen Zahlen und einiger verwandten Reihen", Sitzungsber. Münch. Akad. 4: 157–187.
- Slavutskii, Ilya Sh. (1995), "Staudt and arithmetical properties of Bernoulli numbers", Historia Scientiarum 2: 69–74.
- von Staudt, K. G. Ch. (1840), "Beweis eines Lehrsatzes, die Bernoullischen Zahlen betreffend", Journal für die reine und angewandte Mathematik 21: 372–374.
- von Staudt, K. G. Ch. (1845), "De numeris Bernoullianis, commentationem alteram", Erlangen.
- Sun, Zhi-Wei (2005/2006), Some curious results on Bernoulli and Euler polynomials, http://pweb.nju.edu.cn/zwsun.
- Woon, S. C. (1998), Generalization of a relation between the Riemann zeta function and Bernoulli numbers, http://arXiv.org/abs/math.NT/9812143
- Worpitzky, J. (1883), "Studien über die Bernoullischen und Eulerschen Zahlen", Journal für die reine und angewandte Mathematik 94: 203–232.
وصلات خارجية
- The first 498 Bernoulli Numbers from Project Gutenberg
- The first 10,000 Bernoulli numbers
- A multimodular algorithm for computing Bernoulli numbers
- The Bernoulli Number Page
- Bernoulli number programs at LiteratePrograms
- Dilcher, K.; Skula, L.; Slavutskii, I. Sh. (1991), "Bernoulli numbers. Bibliography (1713-1990)", Queen's Papers in Pure and Applied Mathematics (Kingston, Ontario) (87), http://www.mscs.dal.ca/~dilcher/bernoulli.html
- Eric W. Weisstein, Bernoulli Number at MathWorld.
- The Computation of Irregular Primes
- Online Bernoulli Numbers Generator
- Some properties,sums of Bernoulli-and related numbers






























![{\displaystyle \left[{\begin{matrix}n\\m\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/445b90c841dacb5b557b4032ae75f6f07b3a7b3a)
![{\displaystyle {\frac {1}{m!}}\sum _{k=0}^{m}(-1)^{k}\left[{\begin{matrix}m+1\\k+1\end{matrix}}\right]B_{k}={\frac {1}{m+1}}\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1880891f35ca83e958c86c3298862fb4e2f93646)
![{\displaystyle {\frac {1}{m!}}\sum _{k=0}^{m}(-1)^{k}\left[{\begin{matrix}m+1\\k+1\end{matrix}}\right]B_{n+k}=A_{n,m}\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/615020fad3ae57e7608c308d83a9d5a4c08d1631)


![{\displaystyle B_{2n}=(-1)^{n+1}{\frac {2(2n)!}{(2\pi )^{2n}}}\left[1+{\frac {1}{2^{2n}}}+{\frac {1}{3^{2n}}}+{\frac {1}{4^{2n}}}+\cdots \;\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42b800ebe6859133a505f8634cc2ab6da61605e5)









![{\displaystyle B_{n}=(-1)^{\left\lfloor n/2\right\rfloor }\left[n\ \operatorname {even} \right]{\frac {n!}{2^{n}-4^{n}}}\,S_{n}\ ,\quad (n=2,3,\ldots )\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3ea3f2c1f36c215291b1471bb790e466da93f2f)
![{\displaystyle E_{n}=(-1)^{\left\lfloor n/2\right\rfloor }\left[n\ \operatorname {even} \right]n!\,S_{n+1}\quad \qquad (n=0,1,\ldots )\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc137d852492a5d44f45124f89484067df1d022c)


![{\displaystyle B_{n}=(-1)^{\left\lfloor n/2\right\rfloor }\left[n{\text{ even}}\right]{\frac {n}{2^{n}-4^{n}}}\,T_{n}\ ,\quad (n=2,3,\ldots )\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a7ca47710014bd1fdc5fdd58b2fcb7953fa1e9d)
![{\displaystyle E_{n}=(-1)^{\left\lfloor n/2\right\rfloor }\left[n{\text{ even}}\right]T_{n+1}\quad \quad \qquad (n=0,1,\ldots )\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba0b7ab9957985520df60ad0ee30977c32b45a5)
































![{\displaystyle -1+\sum _{k=0}^{n}{\binom {n}{k}}{\frac {2^{n-k+1}}{n-k+1}}B_{k}(0)=[n=0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fb1e16f3822e3b947f8eeaa3200acba7f6d1550)
