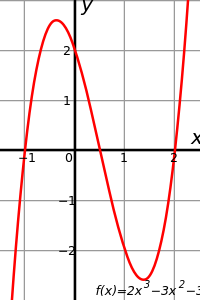
معادلة تكعيبية

هذا المقال هو عن cubic equations in one variable. إذا كنت تريد cubic equations in two variables، انظر cubic plane curve.

In algebra, a cubic function is a function of the form

Graph of a cubic function with 3 real roots (where the curve crosses the horizontal axis—where y = 0) (and hence no complex roots). The case shown has two critical points. Here the function is ƒ(x) = (x³ + 3x² − 6x − 8) / 4. There would be only one real root, and two complex roots, if the local minimum were above the x axis, or if the local maximum were below the x axis, or if there were no local minimum or maximum and the inflection point were off the x axis.

$f(x)=ax^{3}+bx^{2}+cx+d,\,$

where a is nonzero. In other words, a cubic function is defined by a polynomial of degree three.

Setting ƒ(x) = 0 produces a cubic equation of the form:

$ax^{3}+bx^{2}+cx+d=0.\,$

Usually, the coefficients a, b, c, d are real numbers. However much of the theory of cubic equations for real coefficients applies to other types of coefficients (such as complex ones).

Solving the cubic equation is equivalent to finding the particular value (or values) of x for which ƒ(x) = 0. There are various methods to solve cubic equations. The solutions of a cubic equation, also called roots of the cubic function, can always be found algebraically. (This is also true of a quadratic or quartic (fourth degree) equation, but no higher-degree equation, by the Abel–Ruffini theorem). The roots can also be found trigonometrically. Alternatively, one can find a numerical approximation of the roots in the field of the real or complex numbers such as by using root-finding algorithms like Newton's method.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التاريخ

Cubic equations were known to the ancient Babylonians, Greeks, Chinese, Indians, and Egyptians. Babylonian (20th to 16th centuries BC) cuneiform tablets have been found with tables for calculating cubes and cube roots. The Babylonians could have used the tables to solve cubic equations, but no evidence exists to confirm that they did. The problem of doubling the cube involves the simplest and oldest studied cubic equation, and one for which the ancient Egyptians did not believe a solution existed. In the 5th century BC, Hippocrates reduced this problem to that of finding two mean proportionals between one line and another of twice its length, but could not solve this with a compass and straightedge construction, a task which is now known to be impossible. Methods for solving cubic equations appear in The Nine Chapters on the Mathematical Art, a Chinese mathematical text compiled around the 2nd century BC and commented on by Liu Hui in the 3rd century. In the 3rd century, the ancient Greek mathematician Diophantus found integer or rational solutions for some bivariate cubic equations (Diophantine equations). Hippocrates, Menaechmus and Archimedes are believed to have come close to solving the problem of doubling the cube using intersecting conic sections, though historians such as Reviel Netz dispute whether the Greeks were thinking about cubic equations or just problems that can lead to cubic equations. Some others like T. L. Heath, who translated all Archimedes' works, disagree, putting forward evidence that Archimedes really solved cubic equations using intersections of two cones, but also discussed the conditions where the roots are 0, 1 or 2.

Two-dimensional graph of a cubic, the polynomial ƒ(x) = 2x³ − 3x² − 3x + 2.

In the 7th century, the Tang dynasty astronomer mathematician Wang Xiaotong in his mathematical treatise titled Jigu Suanjing systematically established and solved 25 cubic equations of the form $x^{3}+px^{2}+qx=N$, 23 of them with $p,q\neq 0$, and two of them with $q=0$.

In the 11th century, the Persian poet-mathematician, Omar Khayyám (1048–1131), made significant progress in the theory of cubic equations. In an early paper, he discovered that a cubic equation can have more than one solution and stated that it cannot be solved using compass and straightedge constructions. He also found a geometric solution. In his later work, the Treatise on Demonstration of Problems of Algebra, he wrote a complete classification of cubic equations with general geometric solutions found by means of intersecting conic sections.

In the 12th century, the Indian mathematician Bhaskara II attempted the solution of cubic equations without general success. However, he gave one example of a cubic equation:

$x^{3}+12x=6x^{2}+35\,$

In the 12th century, another Persian mathematician, Sharaf al-Dīn al-Tūsī (1135–1213), wrote the Al-Mu'adalat (Treatise on Equations), which dealt with eight types of cubic equations with positive solutions and five types of cubic equations which may not have positive solutions. He used what would later be known as the "Ruffini-Horner method" to numerically approximate the root of a cubic equation. He also developed the concepts of a derivative function and the maxima and minima of curves in order to solve cubic equations which may not have positive solutions. He understood the importance of the discriminant of the cubic equation to find algebraic solutions to certain types of cubic equations.

Leonardo de Pisa, also known as Fibonacci (1170–1250), was able to closely approximate the positive solution to the cubic equation x³ + 2x² + 10x = 20, using the Babylonian numerals. He gave the result as 1,22,7,42,33,4,40 (equivalent to 1 + 22/60 + 7/60² + 42/60³ + 33/60⁴ + 4/60⁵ + 40/60⁶), which differs from the correct value by only about three trillionths.

In the early 16th century, the Italian mathematician Scipione del Ferro (1465–1526) found a method for solving a class of cubic equations, namely those of the form x³ + mx = n. In fact, all cubic equations can be reduced to this form if we allow m and n to be negative, but negative numbers were not known to him at that time. Del Ferro kept his achievement secret until just before his death, when he told his student Antonio Fiore about it.

Niccolò Fontana Tartaglia

In 1530, Niccolò Tartaglia (1500–1557) received two problems in cubic equations from Zuanne da Coi and announced that he could solve them. He was soon challenged by Fiore, which led to a famous contest between the two. Each contestant had to put up a certain amount of money and to propose a number of problems for his rival to solve. Whoever solved more problems within 30 days would get all the money. Tartaglia received questions in the form x³ + mx = n, for which he had worked out a general method. Fiore received questions in the form x³ + mx² = n, which proved to be too difficult for him to solve, and Tartaglia won the contest.

Later, Tartaglia was persuaded by Gerolamo Cardano (1501–1576) to reveal his secret for solving cubic equations. In 1539, Tartaglia did so only on the condition that Cardano would never reveal it and that if he did write a book about cubics, he would give Tartaglia time to publish. Some years later, Cardano learned about Ferro's prior work and published Ferro's method in his book Ars Magna in 1545, meaning Cardano gave Tartaglia 6 years to publish his results (with credit given to Tartaglia for an independent solution). Cardano's promise with Tartaglia stated that he not publish Tartaglia's work, and Cardano felt he was publishing del Ferro's, so as to get around the promise. Nevertheless, this led to a challenge to Cardano by Tartaglia, which Cardano denied. The challenge was eventually accepted by Cardano's student Lodovico Ferrari (1522–1565). Ferrari did better than Tartaglia in the competition, and Tartaglia lost both his prestige and income.

Cardano noticed that Tartaglia's method sometimes required him to extract the square root of a negative number. He even included a calculation with these complex numbers in Ars Magna, but he did not really understand it. Rafael Bombelli studied this issue in detail and is therefore often considered as the discoverer of complex numbers.

François Viète (1540–1603) independently derived the trigonometric solution for the cubic with three real roots, and René Descartes (1596–1650) extended the work of Viète.

 النقاط الحرجة لدالة تكعيبية

الجذور، وturning points, stationary points، نقطة انقلاب وتقعر عديدة الحدود تكعيبية x³ - 3x² - 144x + 432 (الخط الأسود) ومشتقاته الأولى والثانية (الأحمر والأزرق).

The critical points of a cubic equation are those values of x where the slope of the cubic function is zero. They are found by setting derivative of the cubic equation equal to zero obtaining: f ′(x) = 3ax² + 2bx + c = 0. The solutions of that equation are the critical points of the cubic equation and are given by: (using the quadratic formula)

$x={\frac {-b\pm {\sqrt {b^{2}-3ac}}}{3a}}.$

If b² − 3ac > 0, then the cubic function has a local maximum and a local minimum. If b² − 3ac = 0, then the cubic's inflection point is the only critical point. If b² − 3ac < 0, then there are no critical points. In the cases where b² − 3ac ≤ 0, the cubic function is strictly monotonic.

 جذور دالة تكعيبية

The general cubic equation has the form

$ax^{3}+bx^{2}+cx+d=0\qquad (1)$

with $a\neq 0\,.$

This section describes how the roots of such an equation may be computed. The coefficients a, b, c, d are generally assumed to be real numbers, but most of the results apply when they belong to any field of characteristic not 2 or 3.

 طبيعة الجذور

Every cubic equation (1) with real coefficients has at least one solution x among the real numbers; this is a consequence of the intermediate value theorem. We can distinguish several possible cases using the discriminant,

$\Delta =18abcd-4b^{3}d+b^{2}c^{2}-4ac^{3}-27a^{2}d^{2}.\,$

The following cases need to be considered:

• If Δ > 0, then the equation has three distinct real roots.
• If Δ = 0, then the equation has a multiple root and all its roots are real.
• If Δ < 0, then the equation has one real root and two nonreal complex conjugate roots.

For information about the location in the complex plane of the roots of a polynomial of any degree, including degree three, see Properties of polynomial roots and Routh–Hurwitz stability criterion

 صيغة عامة للجذور

For the general cubic equation

$ax^{3}+bx^{2}+cx+d=0$

the general formula for the roots, in terms of the coefficients, is as follows:

$x_{k}=-{\frac {1}{3a}}\left(b\ +\ u_{k}C\ +\ {\frac {\Delta _{0}}{u_{k}C}}\right)\ ,\qquad k\in \{1,2,3\}$

where

$u_{1}=1\ ,\qquad u_{2}={-1+i{\sqrt {3}} \over 2}\ ,\qquad u_{3}={-1-i{\sqrt {3}} \over 2}$

are the three cube roots of unity, and where

$C={\sqrt[{3}]{\frac {\Delta _{1}+{\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}}{2}}}\qquad \qquad {\color {white}.}$ (see below for special cases)

with

${\begin{aligned}\Delta _{0}&=b^{2}-3ac\\\Delta _{1}&=2b^{3}-9abc+27a^{2}d\end{aligned}}$

and

$\Delta _{1}^{2}-4\Delta _{0}^{3}=-27\,a^{2}\,\Delta \ ,$ where $\Delta$ is the discriminant discussed above.

In these formulae, ${\sqrt {~~}}$ and ${\sqrt[{3}]{~~}}$ denote any choice for the square or cube roots. Changing of choice for the square root amounts to exchanging $x_{2}$ and $x_{3}$. Changing of choice for the cube root amounts to circularly permuting the roots. Thus the freeness of choosing a determination of the square or cube roots corresponds exactly to the freeness for numbering the roots of the equation.

Four centuries ago, Gerolamo Cardano proposed a similar formula (see below), which still appears in many textbooks:

$x_{k}=-{\frac {1}{3a}}\left(b\ +\ u_{k}C\ +\ {\bar {u}}_{k}{\bar {C}}\right)$

where

${\bar {C}}={\sqrt[{3}]{\frac {\Delta _{1}-{\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}}{2}}}$

and ${\bar {u}}_{k}$ is the complex conjugate of $u_{k}$ (note that $C{\bar {C}}=\Delta _{0}$).

However, this formula is applicable without further explanation only when a, b, c, d are real numbers and the operand of the square root, i.e., $\Delta _{1}^{2}-4\Delta _{0}^{3}$, is non-negative. When this operand is real and non-negative, the square root refers to the principal (positive) square root and the cube roots in the formula are to be interpreted as the real ones. Otherwise, there is no real square root and one can arbitrarily choose one of the imaginary square roots (the same one everywhere in the solution). For extracting the complex cube roots of the resulting complex expression, we have also to choose among three cube roots in each part of each solution, giving nine possible combinations of one of three cube roots for the first part of the expression and one of three for the second. The correct combination is such that the two cube roots chosen for the two terms in a given solution expression are complex conjugates of each other (whereby the two imaginary terms in each solution cancel out).

The next sections describe how these formulas may be obtained.

 حالات خاصة

If $\Delta \neq 0$ and $\Delta _{0}=0,$ the sign of ${\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}={\sqrt {\Delta _{1}^{2}}}$ has to be chosen to have $C\neq 0,$ that is one should define ${\sqrt {\Delta _{1}^{2}}}=\Delta _{1},$ whichever is the sign of $\Delta _{1}.$

If $\Delta =0$ and $\ \Delta _{0}=0,$ the three roots are equal:

$x_{1}=x_{2}=x_{3}=-{\frac {b}{3a}}.$

If $\Delta =0$ and $\Delta _{0}\neq 0,$ the above expression for the roots is correct but misleading, hiding the fact that no radical is needed to represent the roots. In fact, in this case, there is a double root,

$x_{1}=x_{2}={\frac {9ad-bc}{2\Delta _{0}}},$

and a simple root

$x_{3}={\frac {4abc-9a^{2}d-b^{3}}{a\Delta _{0}}}.$

 الاختزال إلى تكعيبية مضغوطة

Dividing Equation (1) by $a$ and substituting $t-{\frac {b}{3a}}$ for $x$ (the Tschirnhaus transformation) we get the equation

$t^{3}+pt+q=0\qquad (2)$

where

${\begin{aligned}p=&{\frac {3ac-b^{2}}{3a^{2}}}\\q=&{\frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}}.\end{aligned}}$

The left hand side of equation (2) is a monic trinomial called a depressed cubic.

Any formula for the roots of a depressed cubic may be transformed into a formula for the roots of Equation (1) by substituting the above values for $p$ and $q$ and using the relation $x=t-{\frac {b}{3a}}$.

Therefore, only Equation (2) is considered in the following.

 طريقة كاردانو

الحلول يمكن العثور عليها بالطريقة التالية التي اكتشفها سكيپيونى دل فـِرّو و تارتاليا، ونشرها جرولامو كاردانو في 1545.

This method applies to the depressed cubic

$t^{3}+pt+q=0\,.\qquad (2)$

We introduce two variables u and v linked by the condition

$u+v=t\,$

and substitute this in the depressed cubic (2), giving

$u^{3}+v^{3}+(3uv+p)(u+v)+q=0\qquad (3)\,$.

At this point Cardano imposed a second condition for the variables u and v:

$3uv+p=0\,$.

As the first parenthesis vanishes in (3), we get $u^{3}+v^{3}=-q$ and $u^{3}v^{3}=-p^{3}/27$. The combination of these two equations leads to a quadratic equation (since they are the sum and the product of $u^{3}$ and $v^{3}$ ). Thus $u^{3}$ and $v^{3}$ are the two roots of the following quadratic equation:

$z^{2}+qz-{p^{3} \over 27}=0\,.$

At this point, Cardano, who did not know complex numbers, supposed that the roots of this equation were real, that is that ${\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}>0\,.$

Solving this equation and using the fact that $u$ and $v$ may be exchanged, we find

$u^{3}=-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}$ and $v^{3}=-{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}$.

As these expressions are real, their cube roots are well-defined and, like Cardano, we get

$t_{1}=u+v={\sqrt[{3}]{-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}+{\sqrt[{3}]{-{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}.}}$

Given the assumption that ${\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}>0\,,$ Equation (2) also has two complex roots. These are obtained by considering the complex cube roots appearing in the above formula; the fact $uv$ is real implies that one is obtained by multiplying the first of the above cube roots by $\,{\tfrac {-1}{2}}+i{\tfrac {\sqrt {3}}{2}}\,$ and the second by $\,{\tfrac {-1}{2}}-i{\tfrac {\sqrt {3}}{2}}\,$, and vice versa for the other one.

If ${\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}\,$ is not necessarily positive, we have to choose a cube root of $u^{3}$. As there is no direct way to choose the corresponding cube root of $v^{3}$, one has to use the relation $v=-{\frac {p}{3u}}$, which gives

$u={\sqrt[{3}]{-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}\qquad (4)$

and

$t=u-{\frac {p}{3u}}\,.$

Note that the sign of the square root does not affect the resulting $t$, because changing it amounts to exchanging $u$ and $v$. We have chosen the minus sign to have $u\neq 0$ when $p=0$ and $q\neq 0$, in order to avoid a division by zero. With this choice, the above expression for $t$ always works, except when $p=q=0$, where the second term becomes 0/0. In this case there is a triple root $t=0$.

Note also that in several cases the solutions are expressed with fewer square or cube roots

If $p=q=0$ then we have the triple real root

$t=0.\,$

If $p=0$ and $q\neq 0$ then

$u=-{\sqrt[{3}]{q}}{\text{ and }}v=0$

and the three roots are the three cube roots of $-q$.

If $p\neq 0$ and $q=0$ then

$u={\sqrt {p \over 3}}\qquad {\text{and}}\qquad v=-{\sqrt {p \over 3}},$

in which case the three roots are

$t=u+v=0,\qquad t=\omega _{1}u-{p \over 3\omega _{1}u}={\sqrt {-p}},\qquad t={u \over \omega _{1}}-{\omega _{1}p \over 3u}=-{\sqrt {-p}},$

where

$\omega _{1}=e^{i{\frac {2\pi }{3}}}=-{\tfrac {1}{2}}+{\tfrac {\sqrt {3}}{2}}i.$

Finally if $4p^{3}+27q^{2}=0{\text{ and }}p\neq 0$, there are a double root and an isolated root which may be expressed rationally in terms of $p{\text{ and }}q$, but these expressions may not be immediately deduced from the general expression of the roots:

$t_{1}=t_{2}=-{\frac {3q}{2p}}\quad {\text{and}}\quad t_{3}={\frac {3q}{p}}\,.$

To pass from these roots of $t$ in Equation (2) to the general formulas for roots of $x$ in Equation (1), subtract ${\frac {b}{3a}}$ and replace $p$ and $q$ by their expressions in terms of $a,b,c,d$.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التفسير الهندسي للجذور

 ثلاث جذور حقيقية

For the cubic $x^{3}+bx^{2}+cx+d=0$ with three real roots, the roots are the projection on the x-axis of the vertices A, B, and C of an equilateral triangle. The center of the triangle has the same abscissa as the inflection point.

Viète's trigonometric expression of the roots in the three-real-roots case lends itself to a geometric interpretation in terms of a circle. When the cubic is written in depressed form $t^{3}+pt+q=0$, as shown above, the solution can be expressed as

$t_{k}=2{\sqrt {-{\frac {p}{3}}}}\cos \left({\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-k{\frac {2\pi }{3}}\right)\quad {\text{for}}\quad k=0,1,2\,.$

Here $\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)$ is an angle in the unit circle; taking ${\tfrac {1}{3}}$ of that angle corresponds to taking a cube root of a complex number; adding $-k{\frac {2\pi }{3}}$ for k = 1, 2 finds the other cube roots; and multiplying the cosines of these resulting angles by $2{\sqrt {-{\frac {p}{3}}}}$ corrects for scale.

For the non-depressed case $x^{3}+bx^{2}+cx+d=0$ (shown in the accompanying graph), the depressed case as indicated previously is obtained by defining t such that $x=t-{\tfrac {b}{3}}$ so $t=x+{\tfrac {b}{3}}$. Graphically this corresponds to simply shifting the graph horizontally when changing between the variables t and x, without changing the angle relationships. This shift moves the point of inflection and the centre of the circle onto the y-axis. Consequently, the roots of the equation in $t$ sum to zero.

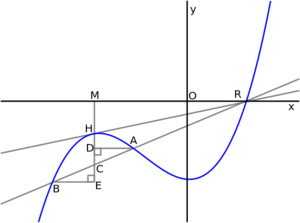
 جذر حقيقي وجذران معقدان

 في المستوى الكارتيزي

The slope of line RA is twice that of RH. Denoting the complex roots of the cubic as g±hi, g = $\scriptstyle {\overline {OM}}$ (negative here) and h = $\scriptstyle {\sqrt {\tan ORH}}$ = $\scriptstyle {\sqrt {\text{slope of line RH}}}$ = $\scriptstyle {\overline {BE}}$ = $\scriptstyle {\overline {DA}}.$

If a cubic is plotted in the Cartesian plane, the real root can be seen graphically as the horizontal intercept of the curve. But further, if the complex conjugate roots are written as $g\pm hi,$ then g is the abscissa (the positive or negative horizontal distance from the origin) of the tangency point of a line that is tangent to the cubic curve and intersects the horizontal axis at the same place as does the cubic curve; and |h| is the square root of the tangent of the angle between this line and the horizontal axis.

 في المستوى المعقد

With one real and two complex roots, the three roots can be represented as points in the complex plane, as can the two roots of the cubic's derivative. There is an interesting geometrical relationship among all these roots.

The points in the complex plane representing the three roots serve as the vertices of an isosceles triangle. (The triangle is isosceles because one root is on the horizontal (real) axis and the other two roots, being complex conjugates, appear symmetrically above and below the real axis.) Marden's Theorem says that the points representing the roots of the derivative of the cubic are the foci of the Steiner inellipse of the triangle—the unique ellipse that is tangent to the triangle at the midpoints of its sides. If the angle at the vertex on the real axis is less than ${\tfrac {\pi }{3}}$ then the major axis of the ellipse lies on the real axis, as do its foci and hence the roots of the derivative. If that angle is greater than ${\tfrac {\pi }{3}}$, the major axis is vertical and its foci, the roots of the derivative, are complex conjugates. And if that angle is ${\tfrac {\pi }{3}}$, the triangle is equilateral, the Steiner inellipse is simply the triangle's incircle, its foci coincide with each other at the incenter, which lies on the real axis, and hence the derivative has duplicate real roots.

 حل عمر الخيام

Omar Khayyám's geometric solution of a cubic equation, for the case a=2, b=16, giving the root 2. The fact that the vertical line intersects the x-axis at the center of the circle is specific to this particular example

As shown in this graph, to solve the third-degree equation $x^{3}+a^{2}x=b$ where $b>0,$ Omar Khayyám constructed the parabola $y=x^{2}/a,$ the circle which has as a diameter the line segment $[0,b/a^{2}]$ of the positive x-axis, and a vertical line through the point above the x-axis, where the circle and parabola intersect. The solution is given by the length of the horizontal line segment from the origin to the intersection of the vertical line and the x-axis.

A simple modern proof of the method is the following: multiplying by x the equation, and regrouping the terms gives

${\frac {x^{4}}{a^{2}}}=x\,({\frac {b}{a^{2}}}-x)\,.$

The left-hand side is the value of y² on the parabola. The equation of the circle being $y^{2}+x\,\left(x-{\frac {b}{a^{2}}}\right)=0,$ the right hand side is the value of y² on the circle.

 تطبيقات

Cubic equations arise in various other contexts.

Marden's theorem states that the foci of the Steiner inellipse of any triangle can be found by using the cubic function whose roots are the coordinates in the complex plane of the triangle's three vertices. The roots of the first derivative of this cubic are the complex coordinates of those foci.

Given the cosine (or other trigonometric function) of an arbitrary angle, the cosine of one-third of that angle is one of the roots of a cubic.

The solution of the general quartic equation relies on the solution of its resolvent cubic.

In analytical chemistry, the Charlot equation, which can be used to find the pH of buffer solutions, can be solved using a cubic equation.

The plastic number, 1.3247... , is the sole real solution of the cubic equation $x^{3}=x+1\,.$

The eigenvalues of a 3×3 matrix are the roots of a cubic polynomial which is the characteristic polynomial of the matrix.

The characteristic equation of a third-order linear difference equation or differential equation is a cubic equation.

In chemical engineering and thermodynamics, cubic equations of state are used to model the PVT (pressure, volume, temperature) behavior of substances.

Kinematic equations involving changing rates of acceleration are cubic.

 انظر أيضاً

• Algebraic equation
• Cubic plane curve
• Linear equation
• Newton's method
• Polynomial
• Quadratic equation
• Quartic equation
• Quintic equation
• Spline (mathematics)
• Van der Waals equation

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 مراجع

• Anglin, W. S.; Lambek, Joachim (1995), "Mathematics in the Renaissance", The Heritage of Thales, Springers, pp. 125–131, ISBN 978-0-387-94544-6, http://books.google.com/?id=mZfXHRgJpmQC&pg=PA125&lpg=PA125&dq=%22mathematics+in+the+renaissance%22+heritage+thales&q  Ch. 24.
• Dence, T. (November 1997), "Cubics, chaos and Newton's method", Mathematical Gazette (Mathematical Association) 81: 403–408, doi:10.2307/3619617, ISSN 0025-5572 
• Dunnett, R. (November 1994), "Newton–Raphson and the cubic", Mathematical Gazette (Mathematical Association) 78: 347–348, doi:10.2307/3620218, ISSN 0025-5572 
• Guilbeau, Lucye (1930), "The History of the Solution of the Cubic Equation", Mathematics News Letter 5 (4): 8–12, doi:10.2307/3027812 
• Jacobson, Nathan (2009), Basic algebra, 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1 
• Mitchell, D. W. (November 2007), "Solving cubics by solving triangles", Mathematical Gazette (Mathematical Association) 91: 514–516, ISSN 0025-5572 
• Mitchell, D. W. (November 2009), "Powers of φ as roots of cubics", Mathematical Gazette (Mathematical Association) 93:  ???, ISSN 0025-5572 
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 5.6 Quadratic and Cubic Equations", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8 
• Rechtschaffen, Edgar (July 2008), "Real roots of cubics: Explicit formula for quasi-solutions", Mathematical Gazette (Mathematical Association) 92: 268–276, ISSN 0025-5572 
• Zucker, I. J. (July 2008), "The cubic equation – a new look at the irreducible case", Mathematical Gazette (Mathematical Association) 92: 264–268, ISSN 0025-5572 

 وصلات خارجية

• Hazewinkel, Michiel, ed. (2001), "Cardano formula", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• History of quadratic, cubic and quartic equations on MacTutor archive.