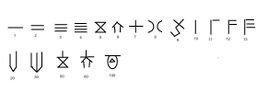
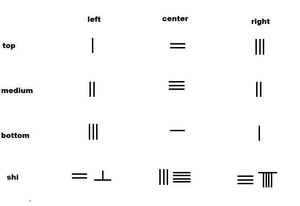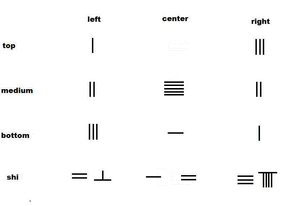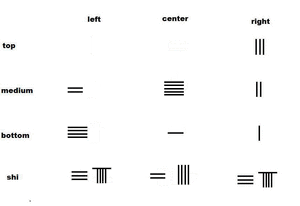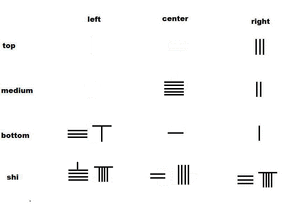
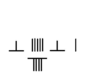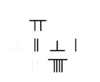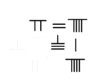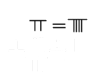الرياضيات الصينية
الرياضيات في الصين emerged independently by the 11th century BC.[1] The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry.
In the Han Dynasty, the Chinese made substantial progress on root extraction and linear algebra.[2] The major texts from the period,The Nine Chapters on the Mathematical Art and the Writings on Reckoning gave detailed processes to solving mathematical problems in daily life.[3] All procedures were computed using a counting board in both texts, and they included negative numbers as well as fractions. The texts provide procedures similar to that Gaussian elimination and Horner's method for linear algebra and solving quadratic equations, respectively.[4] While the Greek mathematics declined in the west during the mediaeval times, the achievement of Chinese algebra reached its zenith in the 13th century, when Zhu Shijie invented the method of four unknowns.
As a result of obvious linguistic and geographic barriers, as well as content, Chinese mathematics and the mathematics of the ancient Mediterranean world are presumed to have developed more or less independently up to the time when The Nine Chapters on the Mathematical Art reached its final form, while the Writings on Reckoning and Huainanzi are roughly contemporary with classical Greek mathematics. Some exchange of ideas across Asia through known cultural exchanges from at least Roman times is likely. Frequently, elements of the mathematics of early societies correspond to rudimentary results found later in branches of modern mathematics such as geometry or number theory. The Pythagorean theorem for example, has been attested to the time of the Duke of Zhou. Knowledge of Pascal's triangle has also been shown to have existed in China centuries before Pascal,[5] such as the Song dynasty Chinese polymath Shen Kuo.
 |
| تاريخ العلوم والتكنولوجيا في الصين |
|---|
| حسب الموضوع |
| حسب الفترة |
خلف العالم الرياضي المعمر جينگ فانگ Jing Fang (عاش 78–37 ق.م.) وراءه كتاباً في الجبر والهندسة، الفصول التسع في فن الرياضيات en ، فيه أول إشارة معروفة للكميات السالبة. وقد حسب دزو تسو تشونج- جي القيمة الصحيحة للنسبة "ط" التقريبية إلى ثلاثة أرقام عشرية، وحسن المغنطيس أو "الأداة التي تشير إلى الجنوب"، وقد وردت إشارة عنه غير واضحة قيل فيها إنه كان يجري التجارب على سفينة تتحرك بنفسها.
الرياضيات الصينية المبكرة

رياضيات چين
لا نعرف الكثير عن رياضيات أسرة چين، أو قبل ذلك، بسبب حرق الكتب ودفن الدارسين.
رياضيات هان
In the Han dynasty, numbers were developed into a place value decimal system and used on a counting board with a set of counting rods called chousuan, consisting of only nine symbols with a blank space on the counting board representing zero.[6] Negative numbers and fractions were also incorporated into solutions of the great mathematical texts of the period.[7] The mathematical texts of the time, the Suàn shù shū and the Jiuzhang suanshu solved basic arithmetic problems such as addition, subtraction, multiplication and division.[7] Furthermore, they gave the processes for square and cubed root extraction, which eventually was applied to solving quadratic equations up to the third order.[8] Both texts also made substantial progress in Linear Algebra, namely solving systems of equations with multiple unknowns.[9] The value of pi is taken to be equal to three in both texts.[10] However, the mathematicians Liu Xin (d. 23) and Zhang Heng (78–139) gave more accurate approximations for pi than Chinese of previous centuries had used.[7] Mathematics was developed to solve practical problems in the time such as division of land or problems related to division of payment.[11] The Chinese did not focus on theoretical proofs based on geometry or algebra in the modern sense of proving equations to find area or volume.[12] The Book of Computations and The Nine Chapters on the Mathematical Art provide numerous practical examples that would be used in daily life.[12]
سوان شو شو
سوان شو شو (كتابات في reckoning) هو نص بالصينية القديمة في الرياضيات يبلغ طوله نحو سبعة آلاف حرف، مكتوب على 190 شريحة من البوص.[13] It was discovered together with other writings in 1984 when archaeologists opened a tomb at Zhangjiashan in Hubei province. From documentary evidence this tomb is known to have been closed in 186 BC, early in the Western Han dynasty.[7] While its relationship to the Nine Chapters is still under discussion by scholars, some of its contents are clearly paralleled there. The text of the Suan shu shu is however much less systematic than the Nine Chapters, and appears to consist of a number of more or less independent short sections of text drawn from a number of sources.[13]
The Book of Computations contains many perquisites to problems that would be expanded upon in The Nine Chapters on the Mathematical Art.[13] An example of the elementary mathematics in the Suàn shù shū, the square root is approximated by using false position method which says to "combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend."[13] Furthermore, The Book of Computations solves systems of two equations and two unknowns using the same false position method.[9]
الفصول التسعة في الفن الرياضي
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, its oldest archeological date being 179 AD (traditionally dated 1000 BC), but perhaps as early as 300–200 BC.[14] Although the author(s) are unknown, they made a major contribution in the eastern world. Problems are set up with questions immediately followed by answers and procedure.[11] There are no formal mathematical proofs within the text, just a step-by-step procedure.[15] The commentary of Liu Hui provided geometrical and algebraic proofs to the problems given within the text.[6]
The Nine Chapters on the Mathematical Art was one of the most influential of all Chinese mathematical books and it is composed of 246 problems.[14] It was later incorporated into The Ten Computational Canons, which became the core of mathematical education in later centuries.[11] This book includes 246 problems on surveying, agriculture, partnerships, engineering, taxation, calculation, the solution of equations, and the properties of right triangles.[11] The Nine Chapters made significant additions to solving quadratic equations in a way similar to Horner's method.[8] It also made advanced contributions to "fangcheng" or what is now known as linear algebra.[9] Chapter seven solves system of linear equations with two unknowns using the false position method, similar to The Book of Computations.[9] Chapter eight deals with solving determinate and indeterminate simultaneous linear equations using positive and negative numbers, with one problem dealing with solving four equations in five unknowns.[9] The Nine Chapters solves systems of equations using methods similar to the modern Gaussian elimination and back substitution.[9]
The version of The Nine Chapters that has served as the foundation for modern renditions was a result of the efforts of the scholar Dai Zhen. Transcribing the problems directly from Yongle Encyclopedia, he then proceeded to make revisions to the original text, along with the inclusion his own notes explaining his reasoning behind the alterations.[4] His finished work would be first published in 1774, but a new revision would be published in 1776 to correct various errors as well as include a version of The Nine Chapters from the Southern Song that contained the commentaries of Lui Hui and Li Chunfeng. The final version of Dai Zhen's work would come in 1777, titled Ripple Pavilion, with this final rendition being widely distributed and coming to serve as the standard for modern versions of The Nine Chapters.[16] However, this version has come under scrutiny from Guo Shuchen, alleging that the edited version still contains numerous errors and that not all of the original amendments were done by Dai Zhen himself.[4]
حساب "ط"
Problems in The Nine Chapters on the Mathematical Art take pi to be equal to three in calculating problems related to circles and spheres, such as spherical surface area.[14] There is no explicit formula given within the text for the calculation of pi to be three, but it is used throughout the problems of both The Nine Chapters on the Mathematical Art and the Artificer's Record, which was produced in the same time period.[10] Historians believe that this figure of pi was calculated using the 3:1 relationship between the circumference and diameter of a circle.[14] Some Han mathematicians attempted to improve this number, such as Liu Xin, who is believed to have estimated pi to be 3.154.[7] Later, Liu Hui attempted to improve the calculation by calculating pi to be 3.141024 (a low estimate of the number). Liu calculated this number by using polygons inside a hexagon as a lower limit compared to a circle.[17] Zu Chongzhi later discovered the calculation of pi to be 3.1415926 < π < 3.1415927 by using polygons with 24,576 sides. This calculation would be discovered in Europe during the 16th century.[18]
There is no explicit method or record of how he calculated this estimate.[7]
القسمة واستخراج الجذور
Basic arithmetic processes such as addition, subtraction, multiplication and division were present before the Han dynasty.[7] The Nine Chapters on the Mathematical Art take these basic operations for granted and simply instruct the reader to perform them.[9] Han mathematicians calculated square and cube roots in a similar manner as division, and problems on division and root extraction both occur in Chapter Four of The Nine Chapters on the Mathematical Art.[19] Calculating the square and cube roots of numbers is done through successive approximation, the same as division, and often uses similar terms such as dividend (shi) and divisor (fa) throughout the process.[8] This process of successive approximation was then extended to solving quadratics of the second and third order, such as , using a method similar to Horner's method.[8] The method was not extended to solve quadratics of the nth order during the Han dynasty; however, this method was eventually used to solve these equations.[8]
الجبر الخطي
The Book of Computations is the first known text to solve systems of equations with two unknowns.[9] There are a total of three sets of problems within The Book of Computations involving solving systems of equations with the false position method, which again are put into practical terms.[9] Chapter Seven of The Nine Chapters on the Mathematical Art also deals with solving a system of two equations with two unknowns with the false position method.[9] To solve for the greater of the two unknowns, the false position method instructs the reader to cross-multiply the minor terms or zi (which are the values given for the excess and deficit) with the major terms mu.[9] To solve for the lesser of the two unknowns, simply add the minor terms together.[9]
Chapter Eight of The Nine Chapters on the Mathematical Art deals with solving infinite equations with infinite unknowns.[9] This process is referred to as the "fangcheng procedure" throughout the chapter.[9] Many historians chose to leave the term fangcheng untranslated due to conflicting evidence of what the term means. Many historians translate the word to linear algebra today. In this chapter, the process of Gaussian elimination and back-substitution are used to solve systems of equations with many unknowns.[9] Problems were done on a counting board and included the use of negative numbers as well as fractions.[9] The counting board was effectively a matrix, where the top line is the first variable of one equation and the bottom was the last.[9]
تعليق ليو هوي على الفصول التسعة في الفن الرياضي
Liu Hui's commentary on The Nine Chapters on the Mathematical Art is the earliest edition of the original text available.[14] Hui is believed by most to be a mathematician shortly after the Han dynasty. Within his commentary, Hui qualified and proved some of the problems from either an algebraic or geometrical standpoint.[12] For instance, throughout The Nine Chapters on the Mathematical Art, the value of pi is taken to be equal to three in problems regarding circles or spheres.[10] In his commentary, Liu Hui finds a more accurate estimation of pi using the method of exhaustion.[10] The method involves creating successive polynomials within a circle so that eventually the area of a higher-order polygon will be identical to that of the circle.[10] From this method, Liu Hui asserted that the value of pi is about 3.14.[7] Liu Hui also presented a geometric proof of square and cubed root extraction similar to the Greek method, which involved cutting a square or cube in any line or section and determining the square root through symmetry of the remaining rectangles.[19]
الرياضيات في فترة التفكك


In the third century Liu Hui wrote his commentary on the Nine Chapters and also wrote Haidao Suanjing which dealt with using Pythagorean theorem (already known by the 9 chapters), and triple, quadruple triangulation for surveying; his accomplishment in the mathematical surveying exceeded those accomplished in the west by a millennium.[20] He was the first Chinese mathematician to calculate π=3.1416 with his π algorithm. He discovered the usage of Cavalieri's principle to find an accurate formula for the volume of a cylinder, and also developed elements of the infinitesimal calculus during the 3rd century CE.
In the fourth century, another influential mathematician named Zu Chongzhi, introduced the Da Ming Li. This calendar was specifically calculated to predict many cosmological cycles that will occur in a period of time. Very little is really known about his life. Today, the only sources are found in Book of Sui, we now know that Zu Chongzhi was one of the generations of mathematicians. He used Liu Hui's pi-algorithm applied to a 12288-gon and obtained a value of pi to 7 accurate decimal places (between 3.1415926 and 3.1415927), which would remain the most accurate approximation of π available for the next 900 years. He also applied He Chengtian's interpolation for approximating irrational number with fraction in his astronomy and mathematical works, he obtained as a good fraction approximate for pi; Yoshio Mikami commented that neither the Greeks, nor the Hindus nor Arabs knew about this fraction approximation to pi, not until the Dutch mathematician Adrian Anthoniszoom rediscovered it in 1585, "the Chinese had therefore been possessed of this the most extraordinary of all fractional values over a whole millennium earlier than Europe"[21]
Along with his son, Zu Geng, Zu Chongzhi applied the Cavalieri's principle to find an accurate solution for calculating the volume of the sphere. Besides containing formulas for the volume of the sphere, his book also included formulas of cubic equations and the accurate value of pi. His work, Zhui Shu was discarded out of the syllabus of mathematics during the Song dynasty and lost. Many believed that Zhui Shu contains the formulas and methods for linear, matrix algebra, algorithm for calculating the value of π, formula for the volume of the sphere. The text should also associate with his astronomical methods of interpolation, which would contain knowledge, similar to our modern mathematics.
A mathematical manual called Sunzi mathematical classic dated between 200 and 400 CE contained the most detailed step by step description of multiplication and division algorithm with counting rods. Intriguingly, Sunzi may have influenced the development of place-value systems and place-value systems and the associated Galley division in the West. European sources learned place-value techniques in the 13th century, from a Latin translation an early-9th-century work by Al-Khwarizmi. Khwarizmi's presentation is almost identical to the division algorithm in Sunzi, even regarding stylistic matters (for example, using blank spaces to represent trailing zeros); the similarity suggests that the results may not have been an independent discovery. Islamic commentators on Al-Khwarizmi's work believed that it primarily summarized Hindu knowledge; Al-Khwarizmi's failure to cite his sources makes it difficult to determine whether those sources had in turn learned the procedure from China.[22]
In the fifth century the manual called "Zhang Qiujian suanjing" discussed linear and quadratic equations. By this point the Chinese had the concept of negative numbers.
رياضيات أسرة تانگ
By the Tang dynasty study of mathematics was fairly standard in the great schools. The Ten Computational Canons was a collection of ten Chinese mathematical works, compiled by early Tang dynasty mathematician Li Chunfeng (李淳風 602–670), as the official mathematical texts for imperial examinations in mathematics. The Sui dynasty and Tang dynasty ran the "School of Computations".[23]
Wang Xiaotong was a great mathematician in the beginning of the Tang dynasty, and he wrote a book: Jigu Suanjing (Continuation of Ancient Mathematics), where numerical solutions which general cubic equations appear for the first time[24]
The Tibetans obtained their first knowledge of mathematics (arithmetic) from China during the reign of Nam-ri srong btsan, who died in 630.[25][26]
The table of sines by the Indian mathematician, Aryabhata, were translated into the Chinese mathematical book of the Kaiyuan Zhanjing, compiled in 718 AD during the Tang dynasty.[27] Although the Chinese excelled in other fields of mathematics such as solid geometry, binomial theorem, and complex algebraic formulas, early forms of trigonometry were not as widely appreciated as in the contemporary Indian and Islamic mathematics.[28]
Yi Xing, the mathematician and Buddhist monk was credited for calculating the tangent table. Instead, the early Chinese used an empirical substitute known as chong cha, while practical use of plane trigonometry in using the sine, the tangent, and the secant were known.[27] Yi Xing was famed for his genius, and was known to have calculated the number of possible positions on a go board game (though without a symbol for zero he had difficulties expressing the number).
رياضيات سونگ و يوان
جيا شيان، الرياضياتي في عهد أسرة سونگ الشمالية، طوّر طريقة تستخدم الضرب والجمع لاستخراج الجذر التربيعي والجذر التكعيبي، وهي تنفذ ما نسميه اليوم "قاعدة هورنر".[29]
الجبر
تسىيوان هايجنگ

تسىيوان هايجنگ (پنين: Cèyuán Hǎijìng) (بالحروف الصينية:測圓海鏡)، أو مرآة البحر لقياسات الدائرة، هي تجميع لـ 692 صيغة و 170 مسألة متعلقة بالدائرة المحفوفة بمثلث، بقلم لي ژي (أو لي يى) (1192–1272 م). وقد استخدم تيان يوان شو لتحويل المشاكل الهندسية المعقدة إلى مشاكل جبرية بحتة. ثم يستخدم فان فا، أو طريقة هورنر، لحل المعادلات من درجات قد تصل حتى الدرجة السادسة، بالرغم من أنه لم يصف طريقته لحل المعادلات.[30] "Li Chih (or Li Yeh, 1192–1279), a mathematician of Peking who was offered a government post by Khublai Khan in 1206, but politely found an excuse to decline it. His Ts'e-yuan hai-ching (Sea-Mirror of the Circle Measurements) includes 170 problems dealing with[...]some of the problems leading to polynomial equations of sixth degree. Although he did not describe his method of solution of equations, it appears that it was not very different from that used by Chu Shih-chieh and Horner. Others who used the Horner method were Ch'in Chiu-shao (ca. 1202 – ca.1261) and Yang Hui (fl. ca. 1261–1275).
مرآة اليشم ذات المجاهيل الأربعة

شي-يوان يو-جيان《四元玉鑒》، أو مرآة اليشم ذات المجاهيل الأربعة، كتبها ژو شيجيى في 1303 م وتمثل سنام التطور في الجبر الصيني. العناصر الأربعة، المسماة السماء والأرض والإنسان والمادة، تمثل الكميات المجهولة الأربع في معادلاته الجبرية. It deals with simultaneous equations and with equations of degrees as high as fourteen. The author uses the method of fan fa, today called Horner's method, to solve these equations.[31]
There are many summation series equations given without proof in the Mirror. A few of the summation series are:[32]
دراسة رياضية في تسعة أقسام
شو-شو تشيو-تشانگ، أو دراسة رياضية في تسعة أقسام، كتبها الوالي الثري والوزير تشين تشيو-شاو (ح. 1202 – ح. 1261 م) وباختراع طريقة لحل المتطابقات الآنية، فقد كانت أوج التحليل غير المحدد الصيني.[33]
المربعات السحرية والدوائر السحرية
أقدم مربعات سحرية معروفة من درجة أعلى من ثلاثة تـُنسب إلى يانگ هوي (ازدهر حوالي 1261–1275)، الذي عمل مع المربعات السحرية حتى الدرجة العاشرة.[34]
حساب المثلثات
The embryonic state of trigonometry in China slowly began to change and advance during the Song dynasty (960–1279), where Chinese mathematicians began to express greater emphasis for the need of spherical trigonometry in calendarical science and astronomical calculations.[27] The polymath Chinese scientist, mathematician and official Shen Kuo (1031–1095) used trigonometric functions to solve mathematical problems of chords and arcs.[27] Victor J. Katz writes that in Shen's formula "technique of intersecting circles", he created an approximation of the arc of a circle s by s = c + 2v2/d, where d is the diameter, v is the versine, c is the length of the chord c subtending the arc.[35] Sal Restivo writes that Shen's work in the lengths of arcs of circles provided the basis for spherical trigonometry developed in the 13th century by the mathematician and astronomer Guo Shoujing (1231–1316).[36] As the historians L. Gauchet and Joseph Needham state, Guo Shoujing used spherical trigonometry in his calculations to improve the calendar system and Chinese astronomy.[27][37] Along with a later 17th-century Chinese illustration of Guo's mathematical proofs, Needham states that:
- Guo used a quadrangular spherical pyramid, the basal quadrilateral of which consisted of one equatorial and one ecliptic arc, together with two meridian arcs, one of which passed through the summer solstice point...By such methods he was able to obtain the du lü (degrees of equator corresponding to degrees of ecliptic), the ji cha (values of chords for given ecliptic arcs), and the cha lü (difference between chords of arcs differing by 1 degree).[38]
Despite the achievements of Shen and Guo's work in trigonometry, another substantial work in Chinese trigonometry would not be published again until 1607, with the dual publication of Euclid's Elements by Chinese official and astronomer Xu Guangqi (1562–1633) and the Italian Jesuit Matteo Ricci (1552–1610).[39]
تطورات لاحقة
إلا أنه بعد الإطاحة بأسرة يوان، أضحت الصين مرتابة من المعرفة التي تستخدمها. وابتعدت أسرة مينگ عن الرياضيات والفيزياء لصالح علم النبات وعلم الصيدلة.
واخترع ژانگ هنگ Zhang Heng آلة لتسجيل الزلازل (سيزموغرافيا) في عام 132م . ولكن علم الطبيعة الصيني قد ضلت معظم أبحاثه في دياجير الـفنگ شوي السحرية والين واليانگ من أبحاث ما وراء الطبيعة . وأكبر الظن أن علماء الرياضة الصينيين قد أخذوا الجبر عن علماء الهند، ولكنهم هم الذين أنشئوا علم الهندسة في بلادهم مدفوعين إلى هذا بحاجتهم إلى قياس الأرض. وكان في وسع الفلكيين في أيام كنفوشيوس أن يتنبئوا بالخسوف والكسوف تنبؤاً دقيقاً، وأن يضعوا أساس التقويم الصيني بتقسيم اليوم إلى اثنتي عشرة ساعة وتقسيم السنة إلى اثني عشر شهراً يبدأ كل منها بظهور الهلال، وكانوا يضيفون شهراً آخر في كل بضع سنين لكي يتفق التقويم القمري مع الفصول الشمسية(71). وكانت حياة الصينيين على الأرض تتفق والحياة في السماء؛ وكانت أعياد السنة تحددها منازل الشمس والقمر، بل إن نظام المجتمع من الناحية الأخلاقية كان يقوم على منازل الكواكب السيارة والنجوم.
نصوص رياضية
أسرة ژو
Zhoubi Suanjing" c. 1000 BCE-100 CE -Astronomical theories, and computation techniques -Proof of the Pythagorean theorem (Shang Gao Theorem) -Fractional computations -Pythagorean theorem for astronomical purposes
Nine Chapters of Mathematical Arts1000 BCE? – 50 CE -ch.1, computational algorithm, area of plane figures, GCF, LCD -ch.2, proportions -ch.3, proportions -ch.4, square, cube roots, finding unknowns -ch.5, volume and usage of pi as 3 -ch.6, proportions -ch,7, interdeterminate equations -ch.8, Gaussian elimination and matrices -ch.9, Pythagorean theorem (Gougu Theorem)
الرياضيات في التعليم
The first reference to a book being used in learning mathematics in China is dated to the second century CE (Hou Hanshu: 24, 862; 35,1207). We are told that Ma Xu (a youth ca 110) and Zheng Xuan (127-200) both studied the Nine Chapters on Mathematical procedures. C.Cullen claims that mathematics, in a manner akin to medicine, was taught orally. The stylistics of the Suàn shù shū from Zhangjiashan suggest that the text was assembled from various sources and then underwent codification.[40]
انظر أيضاً
الهامش والمراجع
 هذه المقالة تتضمن نصاً من Americanized Encyclopædia Britannica: rev. and amended A dictionary of arts, sciences and literature, to which is added biographies of living subjects. 96 colored maps and numerous illustrations, Volume 9، وهي مطبوعة من سنة 1890 وهي الآن مشاع عام في الولايات المتحدة.
هذه المقالة تتضمن نصاً من Americanized Encyclopædia Britannica: rev. and amended A dictionary of arts, sciences and literature, to which is added biographies of living subjects. 96 colored maps and numerous illustrations, Volume 9، وهي مطبوعة من سنة 1890 وهي الآن مشاع عام في الولايات المتحدة. هذه المقالة تتضمن نصاً من The home encyclopædia: compiled and revised to date from the leading encyclopædias, Volume 18، وهي مطبوعة من سنة 1895 وهي الآن مشاع عام في الولايات المتحدة.
هذه المقالة تتضمن نصاً من The home encyclopædia: compiled and revised to date from the leading encyclopædias, Volume 18، وهي مطبوعة من سنة 1895 وهي الآن مشاع عام في الولايات المتحدة. هذه المقالة تتضمن نصاً من Americanized Encyclopædia Britannica, revised and amended: A dictionary of arts, sciences and literature; to which is added biographies of livings subjects ...، وهي مطبوعة من سنة 1890 وهي الآن مشاع عام في الولايات المتحدة.
هذه المقالة تتضمن نصاً من Americanized Encyclopædia Britannica, revised and amended: A dictionary of arts, sciences and literature; to which is added biographies of livings subjects ...، وهي مطبوعة من سنة 1890 وهي الآن مشاع عام في الولايات المتحدة. هذه المقالة تتضمن نصاً من The encyclopædia britannica: a dictionary of arts, sciences, literature and general information, Volume 26، بقلم Hugh Chisholm، وهي مطبوعة من سنة 1911 وهي الآن مشاع عام في الولايات المتحدة.
هذه المقالة تتضمن نصاً من The encyclopædia britannica: a dictionary of arts, sciences, literature and general information, Volume 26، بقلم Hugh Chisholm، وهي مطبوعة من سنة 1911 وهي الآن مشاع عام في الولايات المتحدة. هذه المقالة تتضمن نصاً من The Encyclopædia Britannica: a dictionary of arts, sciences, and general literature, Volume 23، بقلم Thomas Spencer Baynes، وهي مطبوعة من سنة 1888 وهي الآن مشاع عام في الولايات المتحدة.
هذه المقالة تتضمن نصاً من The Encyclopædia Britannica: a dictionary of arts, sciences, and general literature, Volume 23، بقلم Thomas Spencer Baynes، وهي مطبوعة من سنة 1888 وهي الآن مشاع عام في الولايات المتحدة. هذه المقالة تتضمن نصاً من The Encyclopædia Britannica: a dictionary of arts, sciences, literature and general information, Volume 26، بقلم Hugh Chisholm، وهي مطبوعة من سنة 1911 وهي الآن مشاع عام في الولايات المتحدة.
هذه المقالة تتضمن نصاً من The Encyclopædia Britannica: a dictionary of arts, sciences, literature and general information, Volume 26، بقلم Hugh Chisholm، وهي مطبوعة من سنة 1911 وهي الآن مشاع عام في الولايات المتحدة. هذه المقالة تتضمن نصاً من The Encyclopædia britannica: a dictionary of arts, sciences, and general literature ; the R.S. Peale reprint, with new maps and original American articles, Volume 23، بقلم William Harrison De Puy، وهي مطبوعة من سنة 1893 وهي الآن مشاع عام في الولايات المتحدة.
هذه المقالة تتضمن نصاً من The Encyclopædia britannica: a dictionary of arts, sciences, and general literature ; the R.S. Peale reprint, with new maps and original American articles, Volume 23، بقلم William Harrison De Puy، وهي مطبوعة من سنة 1893 وهي الآن مشاع عام في الولايات المتحدة. هذه المقالة تتضمن نصاً من The Life of the Buddha and the early history of his order: derived from Tibetan works in the Bkah-hgyur and Bstan-hgyur followed by notices on the early history of Tibet and Khoten، بقلم Translated by William Woodville Rockhill, Ernst Leumann, Bunyiu Nanjio، وهي مطبوعة من سنة 1907 وهي الآن مشاع عام في الولايات المتحدة.
هذه المقالة تتضمن نصاً من The Life of the Buddha and the early history of his order: derived from Tibetan works in the Bkah-hgyur and Bstan-hgyur followed by notices on the early history of Tibet and Khoten، بقلم Translated by William Woodville Rockhill, Ernst Leumann, Bunyiu Nanjio، وهي مطبوعة من سنة 1907 وهي الآن مشاع عام في الولايات المتحدة. هذه المقالة تتضمن نصاً من The life of the Buddha: and the early history of his order، بقلم William Woodville Rockhill, Ernst Leumann, Bunyiu Nanjio، وهي مطبوعة من سنة 1884 وهي الآن مشاع عام في الولايات المتحدة.
هذه المقالة تتضمن نصاً من The life of the Buddha: and the early history of his order، بقلم William Woodville Rockhill, Ernst Leumann, Bunyiu Nanjio، وهي مطبوعة من سنة 1884 وهي الآن مشاع عام في الولايات المتحدة.
- ^ Chinese overview
- ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماة:0 - ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماة:1 - ^ أ ب ت Hart, Roger (2011). The Chinese roots of linear algebra. Baltimore, MD: Johns Hopkins University Press. pp. 32–33. ISBN 978-0-8018-9958-4.
- ^ Frank J. Swetz and T. I. Kao: Was Pythagoras Chinese?
- ^ أ ب خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماة:03 - ^ أ ب ت ث ج ح خ د خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماة:12 - ^ أ ب ت ث ج خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماة:22 - ^ أ ب ت ث ج ح خ د ذ ر ز س ش ص ض ط ظ Hart, Roger (January 2011). The Chinese Roots of Linear Algebra. Johns Hopkins University. pp. 11–85. ISBN 978-0801897559.
- ^ أ ب ت ث ج Lennart, Bergren (1997). Pi: A Source Book. New York. ISBN 978-1-4757-2738-8.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ أ ب ت ث Lay Yong, Lam (June 1994). "Nine Chapters on the Mathematical Art: An Overview". Archive for History of Exact Sciences. 47 (1): 1–51. doi:10.1007/BF01881700. JSTOR 41133972. S2CID 123502226.
- ^ أ ب ت Siu, Man-Keung (1993). "Proof and Pedagogy in Ancient China". Educational Studies in Mathematics. 24 (4): 345–357. doi:10.1007/BF01273370. JSTOR 3482649. S2CID 120420378.
- ^ أ ب ت ث Dauben, Joseph W. (2008). "算数書 Suan Shu Shu A Book on Numbers and Computations: English Translation with Commentary". Archive for History of Exact Sciences. 62 (2): 91–178. doi:10.1007/s00407-007-0124-1. JSTOR 41134274. S2CID 125757029.
- ^ أ ب ت ث ج Dauben, Joseph (2013). "九章箅术 "Jiu zhang suan shu" (Nine Chapters on the Art of Mathematics)An Appraisal of the Text, its Editions, and Translations". Sudhoffs Archiv. 97 (2): 199–235. doi:10.25162/sudhoff-2013-0017. JSTOR 43694474. PMID 24707775. S2CID 1159700.
- ^ Straffin, Philip D. (1998). "Liu Hui and the First Golden Age of Chinese Mathematics". Mathematics Magazine. 71 (3): 163–181. doi:10.2307/2691200. JSTOR 2691200.
- ^ Dauben, Joseph W. (2013). "九章箅术 "Jiu zhang suan shu" (Nine Chapters on the Art of Mathematics) - An Appraisal of the Text, its Editions, and Translations". Sudhoffs Archiv. 97 (2): 18–19. doi:10.25162/sudhoff-2013-0017. ISSN 0039-4564. JSTOR 43694474. S2CID 1159700.
- ^ Hart, Robert (2011). The Chinese Roots of Linear Algebra. Baltimore, MD: Johns Hopkins University Press. p. 39. ISBN 9780801899584.
- ^ Robin, Wilson (2013). "Early Chinese Mathematics". Math Intelligencer. 35 (2): 80. doi:10.1007/s00283-013-9364-x. S2CID 122920358.
- ^ أ ب Yong, Lam Lay (1970). "The Geometrical Basis of the Ancient Chinese Square-Root Method". Isis. 61 (1): 92–102. doi:10.1086/350581. JSTOR 229151. S2CID 145059170.
- ^ Frank J. Swetz: The Sea Island Mathematical Manual, Surveying and Mathematics in Ancient China 4.2 Chinese Surveying Accomplishments, A Comparative Retrospection p63 The Pennsylvania State University Press, 1992 ISBN 0-271-00799-0
- ^ Yoshio Mikami, The Development of Mathematics in China and Japan, chap 7, p. 50, reprint of 1913 edition Chelsea, NY, Library of Congress catalog 61–13497
- ^ Lam Lay Yong (1996). "The Development of Hindu Arabic and Traditional Chinese Arithmetic" (PDF). Chinese Science. 13: 35–54. Archived from the original (PDF) on 2012-03-21. Retrieved 2015-12-31.
- ^ Alexander Karp; Gert Schubring (25 January 2014). Handbook on the History of Mathematics Education. Springer Science & Business Media. pp. 59–. ISBN 978-1-4614-9155-2.
- ^ Yoshio Mikami, Mathematics in China and Japan,p53
- ^
 Chisholm, Hugh, ed. (1911). . دائرة المعارف البريطانية. Vol. 26 (eleventh ed.). Cambridge University Press. p. 926.
Chisholm, Hugh, ed. (1911). . دائرة المعارف البريطانية. Vol. 26 (eleventh ed.). Cambridge University Press. p. 926. {{cite encyclopedia}}: Cite has empty unknown parameter:|coauthors=(help) - ^ Translated by William Woodville Rockhill, Ernst Leumann, Bunyiu Nanjio (1907). The Life of the Buddha and the early history of his order: derived from Tibetan works in the Bkah-hgyur and Bstan-hgyur followed by notices on the early history of Tibet and Khoten. K. Paul, Trench, Trübner. p. 211. Retrieved 2011-07-01.
sixth century the tibetans obtained their first knowledge of arithmetic and medicine from the chinese.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ أ ب ت ث ج Needham, Volume 3, 109.
- ^ Needham, Volume 3, 108-109.
- ^ Martzloff, 142
- ^ (Boyer 1991, "China and India" p. 204)
- ^ (Boyer 1991, "China and India" p. 203)
- ^ (Boyer 1991, "China and India" p. 205)
- ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةBoyer Sea Mirror - ^ (Boyer 1991, "China and India" pp. 204–205) "The same "Horner" device was used by Yang Hui, about whose life almost nothing is known and who work has survived only in part. Among his contributions that are extant are the earliest Chinese magic squares of order greater than three, including two each of orders four through eight and one each of orders nine and ten."
- ^ Katz, 308.
- ^ Restivo, Sal (1992). Mathematics in Society and History: Sociological Inquiries. Dordrecht: Kluwer Academic Publishers. p. 32. ISBN 1-4020-0039-1..
- ^ Gauchet, 151.
- ^ Needham, Volume 3, 109–110.
- ^ Needham, Volume 3, 110.
- ^ Christopher Cullen, "Numbers, numeracy and the cosmos" in Loewe-Nylan, China's Early Empires, 2010:337-8.
المصادر
- Boyer, C. B. (1989). A History of Mathematics. rev. by Uta C. Merzbach (2nd ed.). New York: Wiley,. ISBN 0-471-09763-2.
{{cite book}}: CS1 maint: extra punctuation (link) (1991 pbk ed. ISBN 0-471-54397-7) - Dauben, Joseph W. (2007). "Chinese Mathematics". In Victor J. Katz (ed.). The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. ISBN 978-0-691-11485-9.
- Martzloff, Jean-Claude (1996). A History of Chinese Mathematics. Springer. ISBN 3-540-33782-2.
- Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.