لوغاريتم طبيعي
دالة اللوغاريتم الطبيعي أو النبيري هي دالة اللوغاريتم للأساس e. و هي الدالة الاصلية للدالة على و تنعدم في 1 . نرمز لهذه الدالة ب Log (عدم الخلط مع log و التي ترمز لدالة اللوغاريتم العشري) أو ln بصفة عامة:
| جزء من سلسلة مقالات عن |
| الثابت الرياضي e |
|---|
 |
| الخصائص |
| التطبيقات |
| تعريف e |
|
شخصيات |
|
مواضيع متعلقة |
التاريخ
لاحظ جون ناپيير أنه بحاجة إلى أساس r لمتتالية هندسية لا يؤدي رفعه إلى قوة إلى اختلاف كبير بين حدين متتالين، لأن العثور على عدد يقع بين حدين متتاليين (وهذا ما يقع في أكثر الأحوال) يؤدي التقريب إلى ما قبله أو إلى ما بعده إلى ارتكاب خطأ كبير إذا كان الأساس كبيراً. وهكذا وجد أن الأساس اللازم اختياره يجب أن يكون قريباً من الواحد الصحيح، وطبعاً لا يمكن اختيار الواحد. فاختار نابيير عدداً قريباً من الواحد يساوي 1-1/710، واختار الحد الأول للمتتالية الهندسية العدد 710 لكي يتجنب الكسور، وهذا أمر متبع منذ أيام بطلميوس، فيكون الحد الثاني 710(1- 1/710) = 9999999. وإذا كان N حداً ما من المتتالية الهندسية [1]
N = 107 (1 - 1/107)L
يكون لوغاريتمه حسب تعريف نابيير هو L. فيكون الحد الأول في المتوالية الهندسية هو لوغاريتم 710 هو المبدأ عند نابيير، وهذا يختلف عما هو متبع حالياً. ثم إن أساس اللوغاريتم الذي أخذه نابيير هو:710(1- 1/710) القريب من limn → ∞(1-1/n)n =1/e وليس e.
عبّر نابيير عن أفكاره الرئيسية بالطريقة التي كانت مألوفة عند اليونانيين والمسلمين أي التي تعتمد الشكل الهندسي، فشرح فكرته في تعريف اللوغاريتم بأطوال ولكنها تتفق مع التعريف العددي الذي تقدم. فقد أخذ قطعة مستقيمة AB ونصف مستقيم SR وفرض أن نقطة P تبدأ من A بسرعة 710 وتتحرك على طول القطعة المستقيمة AB التي طولها أيضاً 710 بسرعة متغيِّرة تتناقص متناسبة مع المسافة PB=x. وفرض أيضاً أن النقطة Q تتحرك في الوقت نفسه على نصف المستقيم SR بسرعة ثابتة هي أيضاً 710 التي انطلقت بها النقطة P من A. وغني عن القول أن نابيير نظم جداوله عددياً لا هندسياً. ولكن التمثيل الهندسي كان كافياً في ذلك الزمان لشرح مضمون فكرته
وقد أطلق نابيير على المسافة SQ اسماً نحته من كلمتين يونانيتين هما Logos وarithmus فكانت كلمة logarithm (التي أصبحت بالعربية لوغاريتم) وقال إن طول SQ هو لوغاريتم المسافة PB.
[لتكن....... AC, CD, DE, EF, هي المسافات التي قطعها المتحرك P في أزمنة متتالية متساوية. فقد عرف نابيير ببصيرته أن النسب CB/DB وAB/CB تتوقف فقط على المدة من A إلى C ومن C إلى D إلخ. فهذه النسب متساوية لأن المدد متساوية. وقد بُرهن فيما بعد على صحة ذلك وأن المسافات… AB, CB, DB, EB, FB تشكل متوالية هندسية. أما المسافات التي يقطعها Q على SR في الوقت نفسه فتشكل متوالية عددية].
وقد استخدم نابيير في جداوله اللوغاريتمية - التي نشرها عام 1614 - الكسور العشرية التي كان قد رَوَّج لها الهولندي ستيفن، فأدخل استعمالها إلى كثير من أنحاء أوربا نتيجة لذيوع استعمال جداوله.
والأمر الذي يدعو إلى العجب هو أن نابيير اختار الأساس القريب جداً من ذاك الذي تأخذ به الطبيعة، إذ يُصادف العدد e حالياً في كثير من قوانين الفيزياء. فكيف ساير تفكير الإنسان دون قصد قوانين الطبيعة؟ هذا يدل على مزايا الفكر الرياضي في وصف قوانين الطبيعة.
لا بد أن يُلاحظ هنا أن الجداول اللوغاريتمية التي كانت أكثر تداولاً تعتمد الأساس 10 بدلاً من الأساس e، إلا أن انتشار الحواسيب المحمولة اليوم أبطل تقريباً استعمال هذه الجداول.
خصائص أساسية
اتصال و رتابة دالة اللوغاريتم الطبيعي
نستنتج مما سبق ان الدالة ln معرفة على و قابلة للاشتقاق على هذا المجال و :
ومنه الدالة ln متصلة على و بما ان مشتقتها موجبة قطعا فانها تزايدية قطعا على
عمليات على دالة اللوغاريتم الطبيعي
لتكن f دالة معرفة ب حيث a و x عددان موجبان قطعا. مشتقة هي نفس مشتقة دالة اللوغاريتم الطبيعي اي ان :
وبما أن : f(1) =k فان : ln(a)=k اذن و بصفة عامة :
من تلك الخاصية نستنتج الخاصيات التالية :
- *
كسور متواصلة
بينما لايوجد كسور متواصلة بسيطة، فإنه يوجد كسور متواصلة معممة، بما فيها:
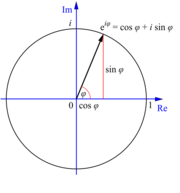
اللوغاريتمات المركبة
 مقالة مفصلة: لوغاريتم مركب
مقالة مفصلة: لوغاريتم مركب
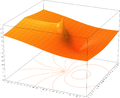
- Plots of the natural logarithm function on the complex plane (principal branch)
انظر أيضاً
- جون ناپييه - مخترع اللوغاريتمات
- دالة تكاملية لوغاريتمية
- نيكولاس مركاتور - أول من استخدم التعبير natural log
- Polylogarithm
- دالة ڤون مونگولت
- العدد e
الهامش
- ^ محمد وائل بشير الأتاسي. "نابيير (جون -)". الموسوعة العربية. Retrieved 2012-05-14.
وصلات خارجية


![{\displaystyle ]0;+\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a2b9afa8192cc3f8173fadddad0d1f5c499d881)




![{\displaystyle \forall (a;b)\in ]0:+\infty [^{2},\ \ln(ab)=\ln(a)+\ln(b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b82a9f70dc4d37520a622aa11d284072b8940537)
![{\displaystyle \forall (a;b)\in ]0:+\infty [^{2},\ \ln \left({\frac {a}{b}}\right)=\ln(a)-\ln(b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be7a5b58797e75ef324c761d5000fddeb7651f6e)
![{\displaystyle \forall a\in ]0;+\infty [,\ \forall n\in \mathbb {Z} ,\ \ln(a^{n})=n\ln(a)\quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fe7b03e53a0c6b3ea568d99f46c042bc48c96b9)
![{\displaystyle \forall a\in ]0;+\infty [,\ \forall r\in \mathbb {Q} ,\ \ln(a^{r})=r\ln(a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38cef3f3f5057e91f503c68cbb07f8afc8a63d8d)
![{\displaystyle \forall (a_{1},a_{2},....,a_{k})\in ]0:+\infty [^{k},\ \sum _{n=1}^{k}ln(a_{n})=ln(\prod _{n=1}^{k}a_{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a211ef5ad7c0bd2944e248b9b138519c4952edc)