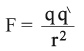كمون كهربائي
| كهرومغناطيسية | ||||||||||

| ||||||||||
كهرباء • مغناطيسية
| ||||||||||
الكمون الكهربائي Electric potential يقصد به مقدار الطاقة الكهربائية الكامنة لدى كل كولوم, حيث الكولوم هو وحدة قياس الشحنة الكهربية في جسيم ما, و مقدار الشحنة التي يحملها الإلكترون مساوية تماما لشحنة البروتون و هي بالتقريب 1.602 × 10–19 كولوم.
حيث وحدة قياس الجهد الكهربي هي فولت و يعرف فرق الجهد الكهربي بين نقطتين مختلفتين بالجهد الكهربي, و دائما تسري حاملات الشحنة السالبة - وهي الإلكترونات - من القطب السالب إلى القطب الموجب . ولكن قبل اكتشاف الإلكترون ومعرفة حقيقة أنه هو بذاته الذي يشكل سريان التيار ، كان تعريف سير التيار الكهربائي قد وقع ، وهو كما تعودنا أن نقول أن التيار ينتقل من القطب الموجب إلى القطب السالب.
يمكن حساب شدة المجال الكهربي حول شحنة بطريقة أخرى، حسب قانون كولوم فإن الكولوم الواحد يخلق حوله مجالا كهربيا يمكن حسابه بالقانون التالي.
حيث E هي المجال الكهربي و وحدة قياسه نيوتن/كولوم أو فولت/متر
أي أن شدة المجال الكهربي تتناسب تناسبا عكسيا ً مع مربع المسافة بين الشحنة الكهربية ونقطة المشاهدة.
و بإجراء عملية تكامل مغلق على هذا المجال الكهربي بالنسبة لطوله يمكن حساب قيمة الجهد الكهربي الناشئ عنه.
خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi_ \mathrm{E} = -\oint_C \mathbf{E} \cdot d\mathbf{l}}
والإشارة السالبة تظهر هنا لأن الإلكترون يحمل شحنة كهربية سالبة فيسري دائما عكس اتجاه المجال الكهربي بينما البروتون حامل الشحنة الموجبة دائما يجري في نفس اتجاه المجال الكهربي وهذا التكامل هو الصورة التكاملية من معادلة ماكسويل الثالثة.
مفهوم الكمون
لمفهوم الكُمون أهمية بالغة في الفيزياء، فهو يرد عند الحديث عن قوى الثقالة gravity وقوى التدافع والتجاذب الكهربائية، أي قوة كولون، كما يرد في فروع أخرى من فروع الفيزياء.
إن نقل جسم كتلته m من نقطة A على سطح الأرض حيث قيمة التسارع الأرضي g إلى نقطة B تبعد عنها مسافة عمودية h، يتطلب بذل عمل مقداره mgh يختزنه الجسم بشكل طاقة كامنة potential energy، فإذا أُتيح للجسم بأن يهوي من جديد أعاد هذه الطاقة، وتكون الطاقة الكامنة الثقالية لواحدة الكتل مساوية gh ويسمى هذا المقدار الكمون الثقالي قريباً من سطح الأرض ويرمز له بـ V. فإذا هبط الجسم من موضع الكمون فيه V1 إلى موضع الكمون فيه V2، قام بعمل W12 يعطى بالعلاقة:
(1)W12 = m (V1- V2) = mg (h1- h2)
وإذا كان مقدار ابتعاد الجسم h عن سطح الأرض كبيراً، فإنه يمكن تعريف تابع كمون V بدلالة التسارع الثقالي g0 قريباً من سطح الأرض بالعلاقة:
(2)V = g0 R2/ (R + h)
حيث ترمز R إلى نصف قطر الأرض. ولتابع الكمون هذا خصائص تابع الكمون نفـسها قريباً من سطح الأرض، فإذا انتقل جسم من الارتفاع h1 إلى الارتفاع h2 فوق سـطح الأرض، فإنه يقـوم بعمـلW12 يتحدد بالطريقة ذاتها ويكون:
(3)
لتابعي الكمون السابقين مزية ألا وهي استقلال العمل المحسوب منهما عن الطريق الذي يسلكه الجسم بين الوضعين الابتدائي والنهائي، وهذا ما يسهل توضيحه في حالة جسم قريب من سطح الأرض مثلاً، فالعمل الناجم عن انتقال الجسم في الشكل (1) بين النقطتين B وA، يساوي مجموع الأعمال الناشئة عن الانتقالات BE وED وDC وCA. إلا أن العمل على كل من الطريقين EB وCD معدوم لتعامد القوة على اتجاه الطريق، ويبقى فقط العمل على كل من ED وCA وهو يساوي mgh وضوحاً.
وثمة ميزة أخرى لتابع الكمون، وهي أن العمل المحسوب منه مستقل عن مبدأ قياس الكمون؛ ففي الحالة التي يكون فيها الكمون V مساوياً gh يكون الموضع h=0 أي سطح الأرض هو موضع انعدام الكمون، فإذا اختير الموضع h=h0 لانعدام الكمون فإن الكمون في هذه الحالة يعطى بالعلاقة:
V = g(h - h0)
ويكون عندها العمل الناجم عن انتقال جسم في حقل الثـقالة الأرضية بين نقطتين h = h1 وh = h2 معطى بالعلاقة:
(4)W12 = g(h1- h0) - g(h2- h0)
W12= g(h1- h2)
وهذا ما تؤكده العلاقة (1). واضح أن واحدة الكمون الثقالي هي Joule/kg.
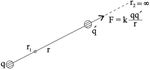
يمكن معالجة الكمون الكهربائي بأسلوب مماثل. إن تحريك شحنة كهربائية q' في حقل شحنة كهربائية أخرى q من إشارة واحدة مثلاً، يتطلب التغلب على قوة تدافع كهربائية، وتظهر هي قوة كولون التي تعطى بالعلاقة:
وذلك باعتبار r البعد بين الشحنتين وk ثابت قيمته 9 × 10 9 في الجملة الدولية.
وإذا تركت الشحنة q' وشأنها من الموضع الذي بلغته أي r=r1 كي تنطلق إلى الموضع r = r2 فإنها تقوم بعمل هو:
ويلاحظ هنا كذلك أن العمل مستقل عن الطريق المسلوك بين النقطتين r1 وr2.
يعرَّف الكمون في النقطة r على أنه الطاقة الكامنة لواحدة الشحنة، وعليه يكون الكمون في الموضع الذي يبعد عن الشحنة q' مسافة r مساوياً لـ:
(5)
يلاحظ من هذا أن: V = 0 عندما ∞r = ، إلا أن الأمر لايتغير أبداً فيما لو اختير موضع آخر مثلاً r = r0 موضعاً للكمون المعدوم، وذلك لأن المهم هو فرق الكمون بين الموضعين المدروسين وهو لايختلف أبداً، شأنه في ذلك شأن الكمون الثقالي.
يـشار هنا إلى أن واحدة الكمون هي جول/كولون أي (J/C) وقد رمز لهذه الواحدة بالاسم فولط ورمزه V، وقد تسـتخدم أجزاؤه الميلي فولط (M1mV= 10-3 V) أو الميـكرو فـولط (V1μV= 10-6 V)، كما تستخدم مضاعفاته الكيلو فولط (K1kV= 103V) أو الميـغا فولـط (M1MV= 106 V).
يقاس الكمون وفرق الكمون كذلك بمقاييس الفولط أو بمقاييس الكهربية electrometers أو باستخدام جسور كهربائية مناسبة حيث يجري البحث عن نقطة توازنها.
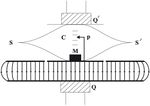
ويظهر في الشكل (3) مقياس للكهربية، يتألف من لوحين دائريين معدنيين يستند فيه الجزء المركزي من اللوح العلوي إلى نابض ss'، ويعزل اللوحين قرصان من الكوارتز Q' وQ. توضع كتلة M فوق الجزء المركزي من القرص العلوي حتى يغدو في مستوي جزئه الخارجي، ويدل مؤشر P على ذلك، فإذا طبق فرق الكمون V بين لوحي المكثفة اختل وضع المؤشر P، وتتطلب إعادته إلى وضعه السابق انتزاع جزء من الكتلة M من فوق الجزء المركزي من القرص العلوي، فإذا رمز بـ F إلى وزن الكتلة المنتزعة فإنه يكون:
F = e0V2A/2d2
حيث ترمز ε0 إلى سماحية الفضاء الحر، وA إلى مساحة الجزء المركزي من اللوح العلوي، وd إلى البعد بين لوحي المكثفة، ومنه يستنتج فرق الكمون بين اللوحين، الذي قد يوصل أحدهما بالأرض.[1]
في الكهرباء الساكنة
التعميم في الديناميكا الكهربائية
الوحدات
Galvani potential versus electrochemical potential
 مقالة مفصلة: Galvani potential
مقالة مفصلة: Galvani potential
المصادر
This article or section includes a list of references or external links, but its sources remain unclear because it lacks in-text citations. You can improve this article by introducing more precise citations. |
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd. ed.). Prentice Hall. ISBN 0-13-805326-X.
- Jackson, John David (1999). Classical Electrodynamics (3rd. ed.). USA: John Wiley & Sons, Inc. ISBN 978-0-471-30932-1.
- Wangsness, Roald K. (1986). Electromagnetic Fields (2nd., Revised, illustrated ed.). Wiley. ISBN 9780471811862.
انظر أيضاً
- كمون كهروكيميائي Electrochemical potential
- جهد كهربائي، أو فرق الجهد الكهربائي
- Absolute electrode potential
- Electrochemical potential
- Electrode potential
- Galvani potential
- Mathematical descriptions of the electromagnetic field
- Voltage, or electric potential difference
المصادر
This article includes a list of references, but its sources remain unclear because it has insufficient inline citations. (April 2008) |
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd. ed.). Prentice Hall. ISBN 0-13-805326-X.
- Jackson, John David (1999). Classical Electrodynamics (3rd. ed.). USA: John Wiley & Sons, Inc. ISBN 978-0-471-30932-1.
- Wangsness, Roald K. (1986). Electromagnetic Fields (2nd., Revised, illustrated ed.). Wiley. ISBN 978-0-471-81186-2.