تدفق مغناطيسي
| كهرومغناطيسية | ||||||||||

| ||||||||||
كهرباء • مغناطيسية
| ||||||||||
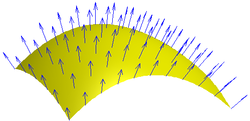
التدفق المغناطيسي الذي يعبر سطح هو عدد خطوط الحقول المغناطيسي والتي تعبر السطح و يعبر عنه بالجداء السلمي لشعاع الحقل المغناطيسي و شعاع السطح
واحده التدفق المغناطيسي هي الويبر Weber، تكريما للفيزيائي الألماني ڤيلهلم ويبر [1804-1891] Wilhelm Eduard Weber.
التدفق المغناطيسي عبارة عن قياس للمغناطيسية مع أخذ قوة و شدة الحقل المغناطيسي بالحسبان.
الوصف
- (uniform B with flat area only)
where θ is the angle between B and a vector a that is perpendicular (normal) to the surface.
In the general case, the magnetic flux through a surface S is defined as the integral of the magnetic field over the area of the surface (See Figures 1 and 2):
where is the magnetic flux, B is the magnetic field,
- S is the surface (area), denotes dot product, and dS is an infinitesimal vector, whose magnitude is the area of a differential element of S, and whose direction is the surface normal. (See surface integral for more details.)
From the definition of the magnetic vector potential A and the fundamental theorem of the curl the magnetic flux may also be defined as:
where the closed line integral is over the boundary of the surface and dℓ is an infinitesimal vector element of that contour Σ.
The magnetic flux is usually measured with a fluxmeter. The fluxmeter contains measuring coils and electronics that evaluates the change of voltage in the measuring coils to calculate the magnetic flux.
Magnetic flux through a closed surface
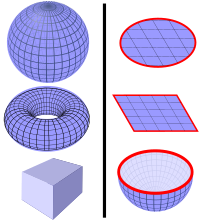
In other words, Gauss's law for magnetism is the statement:
for any closed surface S.
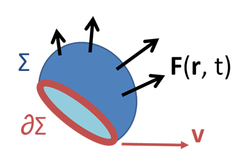
Magnetic flux through an open surface
حيث (انظر الشكل 3):
- is the EMF,
- Φm is the flux through a surface with an opening bounded by a curve ∂Σ(t),
- ∂Σ(t) is a closed contour that can change with time; the EMF is found around this contour, and the contour is a boundary of the surface over which Φm is found,
- dℓ is an infinitesimal vector element of the contour ∂Σ(t),
- v is the velocity of the segment dℓ,
- E is the electric field,
- B is the magnetic field.
مقارنة مع الفيض الكهربائي
By way of contrast, Gauss's law for electric fields, another of Maxwell's equations, is
حيث
- E is the electric field,
- S is any closed surface,
- Q is the total electric charge inside the surface S,
- is the electric constant (a universal constant, also called the "permittivity of free space").
انظر أيضاً
- مجال مغناطيسي
- Maxwell's equations (sometimes called the Maxwell equations) are the set of four equations, attributed to James Clerk Maxwell, that describe the behavior of both the electric and magnetic fields, as well as their interactions with matter.
- Gauss's law gives the relation between the electric flux flowing out a closed surface and the electric charge enclosed in the surface.
- Magnetic circuit is a method using an analogy with electric circuits to calculate the flux of complex systems of magnetic components.
- Magnetic monopole is a hypothetical particle that may be loosely described as "a magnet with only one pole".
- Magnetic flux quantum is the quantum of magnetic flux passing through a superconductor.
- Carl Friedrich Gauss developed a fruitful collaboration with the physics professor Wilhelm Weber; it led to new knowledge in the field of magnetism.
- James Clerk Maxwell demonstrated that electric and magnetic forces are two complementary aspects of electromagnetism.
وصلات خارجية
- براءات اختراع
- Vicci, U.S. Patent 6٬720٬855, Magnetic-flux conduits
- Magnetic Flux through a Loop of Wire by Ernest Lee, Wolfram Demonstrations Project.