عدد مركب

العدد العقدي أو العدد المركب Complex number هو أي عدد على الصورة: حيث أن a و b هما عددان حقيقيان و i هو عدد تخيلي مربعه = -1. و يسمي العدد الحقيقي a بالجزء الحقيقي و العدد الحقيقي b بالجزء التخيلي. فمثلا، 3 + 2i هو عدد عقدي، فيه 3 هو الجزء الحقيقي، و 2 هو الجزء التخيلي.
و عندما يكون b (أي الجزء التخيلي) = 0، فإن قيمة العدد العقدي تساوي قيمة الجزء الحقيقي a فقط و سمي العدد عددًا حقيقيـًا صرفًا Purely real. و عندما يكون a (أي الجزء الحقيقي) = 0، كان العدد تخيليـًا صرفـًا Purely imaginary.
من الممكن إجراء العمليات الحسابية العادية على الأعداد العقدية، كالجمع و الطرح و القسمة و الضرب، تمامًا كالأعداد الحقيقية، و لكنها أيضـًا تتمتع بخصائص أخرى تمكنها من حل كافة المعادلات الجبرية العادية التي يصعب حلها باستخدام الأعداد الحقيقية فقط.
و أحيانـًا قد يكتب العدد العقدي z على الصورة z = a + bj (خصوصـًا في مجال الهندسة الكهربية، لأن i هو رمز التيار الكهربي)
التعريف
العدد العقدي هو الذي يتكون من مجموع عددين، أحدهما عدد حقيقي و الآخر عدد تخيلي، و يكون مربع العدد التخيلي عدد سالب. و يعرف العدد المركب بأنه العدد الذي يمكن وضعه على الصورة:
لمحة تاريخية
ظهرت الأعداد العقدية قبل أن يكتمل وضوح الأعداد السالبة والأعداد غير المنطقة (الصماء)، وكان ذلك عندما حاول الجبريون الإيطاليون في عصر النهضة حل معادلات من الدرجة الثالثة. لقد لاحظ كاردان (1501- 1576) Cardan أنه يمكن أن يكون من بين جذور المعادلة س3+مـ س=ن جذر تربيعي لعدد سالب، وتجرأ بومبلي Bombelli، وهو من رياضيي القرن السادس عشر، فأدخل في حساباته المقدار بفرض أن ب عدد موجب، وسمي هذا المقدار مقداراً مستحيلاً، كما قدم بومبيلي تقريبات للعمليات الحسابية الأساسية الأربع مستخدماً المقدار المستحيل (بعبارات تكاد تكون حديثة). وقبل ألبير جيرار (1595- 1632) Girard الجذور العقدية للمعادلات، وكان أول من أكد أن ن جذر للمعادلة من الدرجة ن، شرط إدخال الجذور المستحيلة ضمن هذا العدد. ولقد رفض ديكارت في هندسته تعبير الأعداد المستحيلة واستخدم بدلاً منه تعبير الجذور التخيلية. تعامل رياضيو القرن السابع عشر مع الأعداد العقدية واستخدموها بثقة كبيرة قبل أن يتأكد الوجود الرياضي للأعداد العقدية، كما أنهم لم يترددوا في استخدام لغرتمات الأعداد التخيلية.
وفي منتصف القرن الثامن عشر برهن دالمبير على إمكان كتابة كل عدد عقدي على النحو ب + ت حـ بفرض أن ب، حـ عددان حقيقيان، كما عمم رياضيو هذا القرن عمليات الأعداد الحقيقية على الأعداد العقدية، ويعود الفضل إلى وسِّل Wessel (عام 1797)، وأرگاند (1768- 1822) Argand في تمثيل الأعداد العقدية بمتجهات مستوية، غير أن گاوس (1798- 1831) Gauss هو الذي وضح العلاقة بين الأعداد العقدية ونقاط المستوي، فكل عدد عقدي ص= ب + ت حـ يقابَل بنقطة من المستوي المنسوب إلى نظام مقارنة ديكارتي قائم ولكن البناء الحدسي لمجموعة الأعداد العقدية لم يرق للجبريين مثل هاملتون (1805- 1865) Hamilton، فحاولوا بناء هذه المجموعة منطقياً انطلاقاً من قاعدة، هي مجموعة الأعداد الحقيقية (على الرغم من أنها لم تكن قد عرفت آنذاك على نحو دقيق). انطلقوا من تعريف الأعداد العقدية على أنها ثنائيات مرتبة (أزواج) من الأعداد الحقيقية.
تمثيل الأعداد المركبة
إذا فرضنا أن z هو عدد مركب، و a و b هما عددان حقيقيان، و i هو عدد تخيلي، فمن الممكن تمثيل العدد المركب z كما يلي:
التمثيل الجبري
يكتب العدد المركب z جبريًا بالشكل:
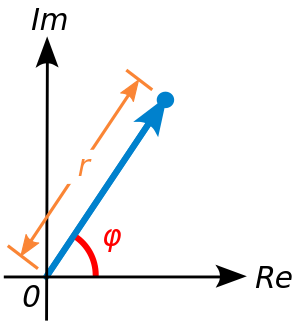
التمثيل الهندسي
يكتب العدد على شكل
التمثيل الأسي
يكتب العدد على شكل
الحساب في مجموعة الأعداد العقدية
الجمع
تتم عملية الجمع كما يلي:
الضرب
تتم عملية الضرب كما يلي
الخارج
تتم عملية القسمة كما يلي:
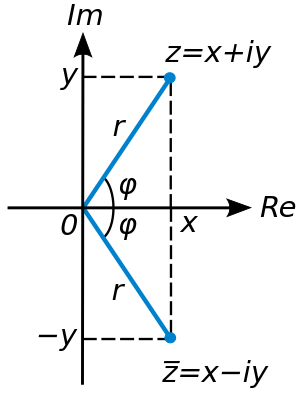
مرافق عدد عقدي
تعريف
مرافق العدد العقدي هو العدد العقدي .

The hue represents the function argument, while the saturation and value represent the magnitude.
مرافق العدد العقدي نرمز له ب:
الأعداد المترافقة و العمليات
- مرافق مجموع عددين عقديين هو مجموع مرافق كل من حدي المجموع
- مرافق جداء عددين عقديين هو جداء مرافق كل من حدي الجداء
معيار عدد عقدي
جدر مربع جداء عدد عقدي في مرافقه يسمى معيار العدد العقدي
التمثيل الهندسي للأعداد العقدية
لحق نقطة
المستوى منسوب لمعلم متعامد ممنظم، التطبيق الذي يربط كل عدد عقدي جزؤه الحقيقي a و جزؤه التخيلي b بالنقطة M من التي أفصولها a و أرتوبها b ، هو تطبيق تقابلي و العدد العقدي يسمى 'لحق' النقطة M.
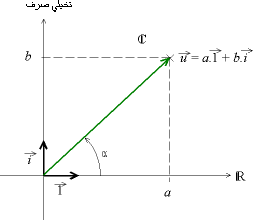
لحق متجهة
المستوى المتجهي منسوب لمعلم متعامد ممنظم، التطبيق الذي يربط كل عدد عقدي جزؤه الحقيقي a و جزؤه التخيلي b بالمتجهة من التي أفصولها a و أرتوبها b ، هو تطبيق تقابلي و العدد العقدي يسمى 'لحق' المتجهة .
- The sum of two points A and B of the complex plane is the point X = A + B such that the triangles with vertices 0, A, B, and X, B, A, are congruent. Thus the addition of two complex numbers is the same as vector addition of two vectors.
- The product of two points A and B is the point X = AB such that the triangles with vertices 0, 1, A, and 0, B, X, are similar.
- The complex conjugate of a point A is the point X = A* such that the triangles with vertices 0, 1, A, and 0, 1, X, are mirror images of each other.
أنظر أيضاً
- Circular motion using complex numbers
- Complex base systems
- Complex geometry
- Complex plane
- De Moivre's formula
- Domain coloring
- Eisenstein integer
- Euler's identity
- Gaussian integer
- Hypercomplex number
- Local field
- Mandelbrot set
- Mathematical diagram
- Quaternion
- Riemann sphere (extended complex plane)
- Split-complex number
- Square root of complex numbers
- Imaginary number/Imaginary unit
المصادر
- Ahlfors, Lars (1979), Complex analysis (3rd ed.), McGraw-Hill, ISBN 978-0070006577
- Conway, John B. (1986), Functions of One Complex Variable I, Springer, ISBN 0-387-90328-3
- Joshi, Kapil D. (1989), Foundations of Discrete Mathematics, New York: John Wiley & Sons, ISBN 978-0-470-21152-6
- Pedoe, Dan (1988), Geometry: A comprehensive course, Dover, ISBN 0-486-65812-0
- Solomentsev, E.D. (2001), "Complex number", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
مصادر تاريخية
- Burton, David M. (1995), The History of Mathematics (3rd ed.), New York: McGraw-Hill, ISBN 978-0-07-009465-9
- Katz, Victor J. (2004), A History of Mathematics, Brief Version, Addison-Wesley, ISBN 978-0-321-16193-2
- Nahin, Paul J. (1998), An Imaginary Tale: The Story of (hardcover ed.), Princeton University Press, ISBN 0-691-02795-1
- A gentle introduction to the history of complex numbers and the beginnings of complex analysis.
- H.-D. Ebbinghaus ... (1991), Numbers (hardcover ed.), Springer, ISBN 0-387-97497-0
- An advanced perspective on the historical development of the concept of number.
قراءات أخرى
- The Road to Reality: A Complete Guide to the Laws of the Universe, by Roger Penrose; Alfred A. Knopf, 2005; ISBN 0-679-45443-8. Chapters 4-7 in particular deal extensively (and enthusiastically) with complex numbers.
- Unknown Quantity: A Real and Imaginary History of Algebra, by John Derbyshire; Joseph Henry Press; ISBN 0-309-09657-X (hardcover 2006). A very readable history with emphasis on solving polynomial equations and the structures of modern algebra.
- Visual Complex Analysis, by Tristan Needham; Clarendon Press; ISBN 0-198-53447-7 (hardcover, 1997). History of complex numbers and complex analysis with compelling and useful visual interpretations.
وصلات خارجية
- Euler's work on Complex Roots of Polynomials at Convergence. MAA Mathematical Sciences Digital Library.
- John and Betty's Journey Through Complex Numbers
- MathWorld articles Complex number and Argand Diagram, and demonstration "Argand Diagram".
- Dimensions: a math film. Chapter 5 presents an introduction to complex arithmetic and stereographic projection. Chapter 6 discusses transformations of the complex plane, Julia sets, and the Mandelbrot set.