سطح زائد
في الرياضيات السطح الزائد (Hyperboloid) هو أحد السطوح الثنائية ثلاثية الأبعاد والذي معادلته كالتالي:
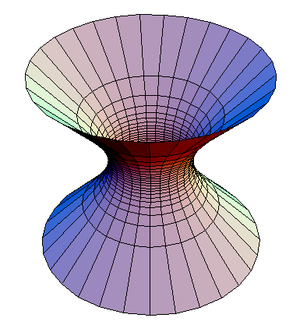
- (سطح زائد ذو طية واحدة),
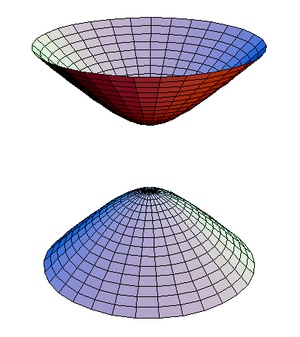
- (سطح زائد ذو طيتان)
إذا وفقط إذا a ساوت b فإن الشكل يسمى سطحا زائدا دورانيا. السطح الزائد ذو الطية الواحدة هو السطح الناشئ من دوران قطع زائد حول محوره المستعرض. يعتبر السطح الزائد ذو الطية الواحدة سطحا مسطرا وإن كان سطحا زائدا دورانيا فإنه بالإمكان الحصول عليه دوران مستقيم حول مستقيم مخالف.
أما السطح الزائد ذو الطيتان للمحور AP فيحصل عليه عن طريق مجموعة النقاط P حيث AP-BP تكون ثابتة، AP هي المسافة بين A وP. تعد A وB بؤرتا السطح الزائد. يمكن الحصول على السطح الزائد ذي الطيتين عن طريق دوران قطع زائد حول محوره البؤري.
السطوح الزائدة المنحلة تكون معادلتها على الشكل:
وفي حالة a تساوي b فإن الشكل الناتج هو مخروط، أما الحالات الأخرى فيطلق على الشكل الناتج مخروط إهليلجي.
منشآت الأسطح الزائدية
One-sheeted hyperboloids are used in construction, with the structures called hyperboloid structures. A hyperboloid is a doubly ruled surface; thus, it can be built with straight steel beams, producing a strong structure at a lower cost than other methods. Examples include cooling towers, especially of power stations, and many other structures.
- Gallery of one sheet hyperboloid structures
The Adziogol Lighthouse, Ukraine, 1911.
Kobe Port Tower, Japan, 1963.
Saint Louis Science Center's James S. McDonnell Planetarium, St. Louis, Missouri, 1963.
Newcastle International Airport control tower, Newcastle upon Tyne, England, 1967.
Cathedral of Brasília, Brazil, 1970.
Hyperboloid water tower with toroidal tank, Ciechanów, Poland, 1972.
Roy Thomson Hall, Toronto, Canada, 1982.
The THTR-300 cooling tower for the now decommissioned thorium nuclear reactor in Hamm-Uentrop, Germany, 1983.
The Corporation Street Bridge, Manchester, England, 1999.
The Killesberg observation tower, Stuttgart, Germany, 2001.
The Canton Tower, China, 2010.
The Essarts-le-Roi water tower, France.