تحويل (دالة)
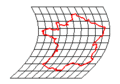
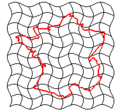
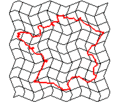
في علم الرياضيات، التحويل إنگليزية: Transformation هي دالة رياضية من مجموعة X إلى نفسها. على الغالب، يكون للمجموعة X هيكلية جبرية أو هندسية أخرى عندها، يصبح تعريف التحويل بالدالة التي تحول X إلى نفسها مع الاحتفاظ بهيكليتها.
من الأمثلة نورد: التحويل الخطي، التحويل الأفيني مثل الدوران، الانعكاس والانزلاق. ويتم تطبيقهم في فضاء إقليدي الثائي والثلاثي الأبعاد. ويمكن أن تؤدى العمليات باستخدام الجبر الخطي وتفسر باستعمال المصفوفات.
الانزلاق
 مقالة مفصلة: انزلاق (هندسة)
مقالة مفصلة: انزلاق (هندسة)
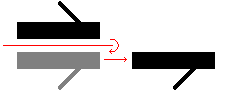
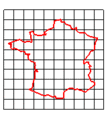
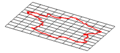
الانزلاق (Translation) هو تحويل أفيني في الفضاء إقليدي بحيث يتم نقل كل نقطة فيه بمسافة محددة وبنفس الاتجاه. ويمكن بوصيفها باضافة المتجه (vector) ثابت لكل نقطة أو بتحريك مركز الإحداثيات.
و بمعنى آخر، إذا كانت v هي موجه ثابت، فان الانزلاق Tv يصبح: Tv(p) = p + v.
الانعكاس
 مقالة مفصلة: انعكاس
مقالة مفصلة: انعكاس
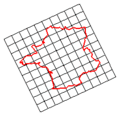
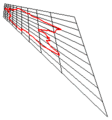
الانعكاس (Reflection أو Reflexion) في الرياضيات هي دالة التي تحول شكل ما إلى صورة مرآته المعكوسة. مثلا، فإن انعكاس شكل الحرف "ع" بالنسبة لخط أفقي يصبح بالشكل "3". لعكس مسطح ثنائي الأبعاد، يستعمل خط كمرآة وحينها يسمى محور الإنعكاس (axis of Reflection) بينما لعكس مسطح ثلاثي الأبعاد، فيستعمل مستوى كمرآة. في بعض الأحيان، يعتبر الانعكاس حالة خاصة من حالات الانقلاب (inversion) ذو قطر لانهائي لدائرة المرجع.
وبالمفهوم الهندسي، لإيجاد الانعكاس لنقطة ما، يتم إسقاط خط عمودي على الخط (أو المستوى) المستعمل كمحور الانعكاس ومن ثم متابعة الخط يشكل مستقيم في الجهة الأخرى وبنفس المسافة. ولتحديد ألانعكاس لرسم ما، يتم تحديد انعكاسات كل النقاط المؤلفة له.
انعكاس انزلاقي
 مقالة مفصلة: انعكاس انزلاقي
مقالة مفصلة: انعكاس انزلاقي
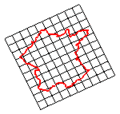
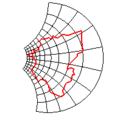
الانعكاس الانزلاقي هي عملية تحويل في الفضاء الإقليدي التي تتشكل من انزلاق ثم انعكاس خطي. في هذه الحالة، تعتبر قيمة المتجه (vector) صفرا.
التحاكي
التحاكي المطرد (Glide reflection) هي عملية تحويل تضخم أو تقلص الأشياء. عامل التحاكي يكون نفسه في كل الاتجاهات.[بحاجة لمصدر]
القص
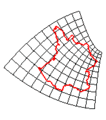
القص (Shear) هي عملية تحويل تتم بدوران أحد المجاور بحيث لا يعود متعامد مع المحور الآخر. فبهذه الحالة، يتحول المستطيل إلى متوازي الأضلاع، والدائرة إلى إهليليج.
تعميم: تحويلات جزئية
بشكل عام، "التحويل" هي أحد أوجه الدالة الرياضية (function). كما يستعمل التعبير إسقاط (mapping) بنفس المعنى.[بحاجة لمصدر] يمكن للتحويل أن يكون دالة إنقلابية (invertible function) من مجموعة X الي مجموهة أخرى Y. وتستعمل مرادفة "التحويل" في العادة في حالة تحويل الهيئات الهندسية أكثر من المعادلات الجبرية.
مفهوم التحويل تم تعميمه إلى الدوال الجزئية. التحويل الجزئي هو الدالة f: A → B، حيث كلاً منA وB عبارة عن مجموعات فرعية في المجموعة X.[1]
بنى جبرية
The set of all transformations on a given base set together with function composition forms a regular semigroup.
توافيق
من أجل المجموعة الكاردينالية المحدودة n، هناك التحوايلات nn والتحويلات الجزئية (n+1)n.[2]
صور
الهامش
- ^ Christopher Hollings (2014). Mathematics across the Iron Curtain: A History of the Algebraic Theory of Semigroups. American Mathematical Society. p. 251. ISBN 978-1-4704-1493-1.
- ^ Olexandr Ganyushkin; Volodymyr Mazorchuk (2008). Classical Finite Transformation Semigroups: An Introduction. Springer Science & Business Media. p. 2. ISBN 978-1-84800-281-4.