هندسة إقليدية

الهندسة الإقليدية تدرس الأشكال و تخضع لمجموعة من المسلمات وضعها إقليدس في كتابه العناصر و هي الهندسة التي تدرس في المدارس والثانويات.
الهندسة الإقليدية لا تستعمل سوى المسطرة والبركار لإنشاء الأشكال وهذا أدى إلى ظهور مسائل هندسية لم يتم حلها إلا في القرن 19 و هذه المسائل هي:
- تقسيم زاوية إلى ثلاثة أقسام متساوية
- إنشاء مكعب حجمه ضعف حجم مكعب معلوم
- إنشاء مربع مساحته تساوي مساحة دائرة معينة
و هذه المسائل يستحيل حلها باستعمال المسطرة والفرجار فقط.
وهو فرع من الرياضيات يهتم بدراسة الأشكال الهندسية التي تقع كل نقاطها في مستوٍ واحد. ومع أن الكلمات: «نقطة» و«مستوي» هي مفاهيم أولية غير مُعرَّفة، فإنه يمكن إعطاء تفسير عملي تطبيقي لها.
العناصر الهندسية
عند النظر إلى الأجسام المحيطة بنا لا يرى منها سوى وجهها؛ إن هذا الوجه هو ما يسمى سطحها. فالسطح ليس له ثخن وإنما هو مجرد وجه ظاهر. ولما كانت الورقة التي يُكتب عليها رقيقة جداً، ويكاد لا يُرى لها ثخن فهي تمثل بصورة تقريبية سطحاً.
ولما كانت الأجسام الصلبة متميزة بأن لها طولاً وعرضاً وارتفاعاً لذلك يقال إن للأجسام الصلبة ثلاثة أبعاد. أما السطح فليس له ارتفاع (أوثخن)، وإنما له طول وعرض فقط، لذلك يقال إن له بعدين.
وليس للخط سوى طول فهو ذو بعد واحد. وقد يكون الخط مستقيماً أو منكسراً أو منحنياً. أما المستقيم فلا يُعرَّف، ولكنه يمثل عادة بخيط مشدود أو بحرف المسطرة. ويمتد من الجهتين من دون وجود نقط ينتهي عندها.
وكذلك النقطة لا تُعرَّف، وإنما تمثل بالأثر الذي يخلفه رأس قلم على سطح ورقة بيضاء أو موضع تقاطع خطين. كل الأشكال الهندسية هي مجموعات من النقط.
ولتسمية المستقيم تختار منه نقطتان ب، جـ ويقرأ المستقيم ب جـ.
نصف المستقيم هو جزء من مستقيم محدود بنقطة ب ويمتد من جهة واحدة.
والقطعة المستقيمة هي جزء من مستقيم محدود بنقطتين.
والخط المنكسر هو خط مكون من عدة قطع مستقيمة متتالية بحيث ترتبط نهاية كل قطعة ببداية التي تليها.
والخط المنحني هو خط غير مستقيم في أي جزء منه.
النقطة
النقطة لا حاجة لتعريفها بواسطة مصطلحات وإنما يمكن تعريفها بواسطة بديهية معينة، كما يمكن تعريفها على أنها كل ما ليس له جزء أو كل مايمكن اهمال ابعاده الثلاثة ويعبر عنها هندسيا بالأثر الذي يتركه القلم عند الضغط عليه بدون تحريكه.
المستقيم

خط يمكن رسمه بالمسطرة و أصغر مسافة بين نقطتين هو مسار مستقيم. ويتكون من ما لانهاية من النقاط
القطعة
خط مستقيم له نقطة بداية وله نقطة نهاية.
نصف مستقيم

يطلق عليه أيضا اسم "الشعاع" وهو جزء من مستقيم محدد بنقطة تسمى أصل نصف المستقيم.
الدائرة

وهي مجموعة نقاط تبعد نفس البعد عن نقطة معينة في نفس المستوي, وهذه النقطة المعينة تدعى مركز الدائرة, والبعد الثابت يدعى نصف قطر الدائرة.
بفرض م نقطة في المستوي و ر عدداً حقيقياً. تسمى مجموعة نقط المستوي التي تبعد عن م مسافة ر دائرة، وتسمى م مركزها و ر نصف قطرها.
وضع نقطة بالنسبة لدائرة: تكون النقطة على الدائرة إذا كان بعدها عن مركزها يساوي نصف القطر، وتكون خارج الدائرة إذا كان بعدها عن المركز أكبر من نصف القطر، وتكون داخل الدائرة إذا كان بعدها أصغر من نصف القطر. فالدائرة منحنٍ مغلق.
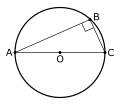
وضع مستقيم بالنسبة لدائرة: إذا كان مستقيم س ع يبعد عن مركز الدائرة بعداً أكبر من نصف قطرها(الشكل 4) تكون جميع نقطه خارج الدائرة. ويكون مماساً للدائرة إذا كان بعده عن مركزها يساوي نصف قطرها. وفي هذه الحال تكون نقطة واحدة (ب) من المستقيم واقعة على الدائرة هي مسقط المركز على المستقيم، وبقية نقط المستقيم كلها خارج الدائرة. ويكون المستقيم س ع قاطعاً للدائرة في نقطتين (ب، جـ) إذا كان بعده عن مركزها م أصغر من نصف قطرها. ولا يمكن أن يشترك مستقيم مع الدائرة بأكثر من نقطتين فالدائرة منحنٍ مغلق محدب، وتسمى القطعة المستقية ب جـ وتراً في الدائرة.
إذا قُسم محيط دائرة م إلى أقسام متساوية بالنقط ب، جـ، د، هـ، و ووصل بينها على التوالي يُحصل على مضلع منتظم محدب أضلاعه متساوية وزواياه متساوية، وإذا لم يُوصل بينها على التوالي يحصل على مضلع منتظم مقعر، يسمى مضلعاً نجمياً .
محيط الدائرة
لما كانت جميع الدوائر متشابهة كانت النسبة بين محيطي دائرتين ح1 و ح2 تساوي النسبة بين قطريهما 2ر1 ، 2ر 2: ح1/ح2= 2ر1/2ر2؛ إذاً ح1/2ر1 = ح2/2ر2.
فإذا أخذت أي دائرة أخرى وجدت النسبة نفسها التي يُرمز لها بالحرف اليوناني π. وقد وجد أن هذه النسبة الثابتة تساوي تقريباً 3.1416 فيمكن أن يكتب بوجه عام ح/2ر = π فمحيط الدائرة ح = 2 π ر.
مساحة الدائرة
لما كانت جميع الدوائر متشابهة كانت مساحاتها متناسبة مع مربعات أنصاف أقطارها. فإذا كانت سط مساحة دائرة ما و ر نصف قطرها تكون النسبة سط/ر2 ثابتة، وقد وجد أنها تساوي π؛ إذاً سط = π ر2.
المستوي والهندسة المستوية
يقال عن سطح إنه مستوٍ إذا انطبق حرف المسطرة المستقيم عليه أينما كان. والهندسة المستوية هي دراسة الأشكال المستوية أي الواقعة في مستوٍ واحد.
ويقاس طول قطعة مستقيمة أو منحنية بمقدار ما تحويه من واحدة الطول.
الزاوية
هي الشكل المكون من نصفي مستقيمين محددين بنقطة واحدة تدعى رأس الزاوية، ويُسمى نصفا المستقيمين ضلعيها.
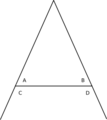
ولتسمية زاوية تختار نقطة على كل ضلع، مثل ب و جـ في الشكل. وتُقرأ ب م جـ الذي يوضع أحياناً على يمينه الرمز < للدلالة على أنه زاوية، وكل من م ب و م جـ ضلع لها. أو يكتفى بذكر الرأس فيكتب < م.
تقاس الزاوية بمقدار ما يدوره أحد ضلعيها لينطبق على الآخر نسبة من الدورة الكاملة. ففي الشكل 1 الزاوية د م ب هي ربع دورة (أو 90 ْ) ويقال إنها قائمة أو إن م د وم ب متعامدان. أما الزاوية ب م جـ فهي أكبر من قائمة، أو يقال منفرجة. وهناك زاوية أخرى ب م جـ يمكن أن يدورها م ب لينطبق على م جـ ولكن في اتجاه معاكس للأول وقد أشير إليها بخط متقطع، وقياسها أكبر من نصف دورة وتسمى منعكسة.
مبادئ الهندسة المستوية
انطلق إقليدس في دراسة الهندسة المستوية من فرضيات رأى أنها واضحة حدساً وبالتجربة، سُميت مصادرات (فرضيات) إقليدس. مثلاً من نقطتين يمر مستقيم واحد فقط.
وينجم عن ذلك أن المستقيمين في مستوٍ واحد إما أن يشتركا بنقطتين فيكونا منطبقين، وإما أن يشتركا بنقطة واحدة ويقال إنهما متقاطعان، وإما ألا يشتركا بأي نقطة ويقال إنهما متوازيان.
ورأى إقليدس أنه في المستوي لا يمكن أن يمر من نقطة خارج مستقيم في هذا المستوي سوى مستقيم واحد يوازي هذا المستقيم. وينتج من ذلك أنه في المستوي إذا قطع مستقيم أحد مستقيمين متوازيين فإنه يقطع الآخر.
المضلعات
يمكن أن يحدد في المستوي مناطق يحد كلاً منها خط منكسر مغلق يسمى مضلعاً. وتسمى كل قطعة من هذا الخط المنكسر ضلعاً. ويقال إن المضلع ثلاثي (أو مثلث) إذا كان له ثلاث أضلاع ، ويقال إنه رباعي إذا كان له أربع أضلاع، وهكذا. ويقال إن المضلع محدب إذا لم يقطعه مستقيم ما بأكثر من نقطتين، أما إذا قطعه بأكثر فيقال إنه مقعر. وهذا الأخير تكون إحدى زواياه منعكسة .
المثلث
هو أبسط المضلعات، ويليه المضلع الرباعي. ولهذا الأخير حالات خاصة وهي متوازي الأضلاع (الذي يكون كل ضلعين متقابلين فيه متوازيين)، ويكون مستطيلاً إذا كانت زواياه قائمة، ويكون معيّناً إذا تساوت أضلاعه ، ويكون مربعاً إذا كانت أضلاعه متساوية وزواياه قائمة..[1]
ومساحة كل من الرباعيات الخاصة الأخيرة تساوي جداء القاعدة في الارتفاع. ولما كان المثلث نصف متوازي أضلاع كانت مساحته هي نصف جداء القاعدة في الارتفاع.
التشابه والتطابق
يقال عن مضلعين إنهما متشابهان إذا كانت زوايا الأول تساوي زوايا الثاني وأضلاع الأول متناسبة مع أضلاع الثاني. وتسمى النسبة بين ضلع من الأول إلى مثيلتها من الثاني نسبة التشابه. وإذا كانت نسبة التشابه تساوي 1 يقال إنهما طبوقان.
تشابه مثلثين:
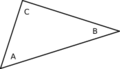
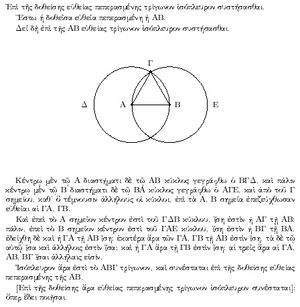
1ـ بما أن مجموع زوايا مثلث ما قائمتين يكفي أن تكون زاويتان من الأول طبوقتين على زاويتين من الثاني لكي يتشابه المثلثان. وإذا كانت ضلع من الأول طبوقةً على مثيلتها من الثاني (أي نسبة التشابه 1) يكون المثلثان طبوقين (الشكل 3).
2ـ كما يتشابه المثلثان إذا تناسبت ضلعان من الأول مع ضلعين من الثاني وكانت الزاوية المحصورة بينهما في الأول طبوقة على مثيلتها من الثاني.
3ـ أو يتشابه المثلثان إذا كانت أضلاع الأول متناسبة مع مثيلاتها من الثاني.
ملاحظة: إن النسبة بين مساحتي مضلعين متشابهين تساوي مربع نسبة التشابه. فالنسبة بين مساحتي المثلثين هي 4/9.
مسلمات إقليدس
- من نقطتين يمر مستقيم وحيد
- المستقيم لا نهاية له أي يمكن تمديد المستقيم من الجهتين إلى ما لانهاية
- من نقطة معينة و من مجال أو قطعة ما هناك قوس دائرة وحيد
- كل الزوايا المستقيمية متساوية فيما بينها
- لا يمر من نقطة سوى مستقيم وحيد موازي لمستقيم معلوم
مسلمة المتوازي
إنشاءات هندسية

بواسطة المسطرة و البركار يمكن إنشاء ما يلي:
- مستقيمين متوازيين
- مستقيمين متعامدين
- منصف زاوية
- واسط قطعة
- دائرة
- قطعة طولها جداء طول قطعتين
- قطعة طولها خارج قسمة طول قطعتين
- قطعة طولها جذر مربع طول قطعة معينة
- زاويتان متساويتان.
برامج لدراسة الهندسة
هناك العديد من البرمجيات المتطورة التي تساهم في دراسة الهندسة الإقليدية المستوية والفراغية وعلى رأسها برنامج السبورة الذكية.
طرق الاثبات
نظام القياس والحساب
تدوين والمصطلحات
تسمية من النقاط والارقام
التكميلية والزوايا التكميلية
الإصدارات الحديثة من التدوين إقليدس
معرض الصور
A surveyor uses a theodolite
Sphere packing applies to a stack of oranges.
Geometry can be used to design origami.
The Bridge of Asses
مثلثات التطابق
مجموع زوايا المثلث
نظرية فيثاغورس =
نظرية تاليس
توسيع نطاق المساحة والحجم
تطبيقات
This section requires expansion. (March 2009) |
Later work
أرشميدس وأبولونيوس
ديكارت في القرن 17
في القرن 18
النسبية العامة في القرن 20
Treatment of infinity
Infinite objects
العمليات اللانهائية
أساس منطقي
This article or section is in need of attention from an expert on the subject. WikiProject Mathematics or the Mathematics Portal may be able to help recruit one. |
This section requires expansion. (June 2010) |
المنطق الكلاسيكي
Modern standards of rigor
تركيبات بديهية
Geometry is the science of correct reasoning on incorrect figures.
— George Polyá، How to Solve It, p. 208
Constructive approaches and pedagogy
انظر أيضاً
- Analytic geometry
- Type theory
- Interactive geometry software
- Non-Euclidean geometry
- Ordered geometry
- Incidence geometry
- Metric geometry
- Birkhoff's axioms
- Hilbert's axioms
- Parallel postulate
- Schopenhauer's criticism of the proofs of the Parallel Postulate
- Cartesian coordinate system
النظريات الكلاسيكية
- Ceva's theorem
- Heron's formula
- Nine-point circle
- Pythagorean theorem
- Menelaus' theorem
- Angle bisector theorem
- Butterfly theorem
هوامش
المصادر
المراجع
- Ball, W.W. Rouse (1960). A Short Account of the History of Mathematics (4th ed. [Reprint. Original publication: London: Macmillan & Co., 1908] ed.). New York: Dover Publications. pp. 50–62. ISBN 0-486-20630-0.
- Coxeter, H.S.M. (1961). Introduction to Geometry. New York: Wiley.
- Euclid, Elements, ca. 300 BCE
- Eves, Howard (1963). A Survey of Geometry. Allyn and Bacon.
- Franzén, Torkel (2005). Gödel's Theorem: An Incomplete Guide to its Use and Abuse. AK Peters. ISBN 1-56881-238-8.
- Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (3 vols.) (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.). New York: Dover Publications. ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3).
{{cite book}}:|format=requires|url=(help); Check|isbn=value: invalid character (help) Heath's authoritative translation of Euclid's Elements plus his extensive historical research and detailed commentary throughout the text. - Hofstadter, Douglas R. (1979). Gödel, Escher, Bach: An Eternal Golden Braid. New York: Basic Books.
- Misner, Thorne, and Wheeler (1973). Gravitation. W.H. Freeman.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Mlodinow (2001). Euclid's Window. The Free Press.
- Nagel, E. and Newman, J.R. (1958). Gödel's Proof. New York University Press.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Alfred Tarski (1951) A Decision Method for Elementary Algebra and Geometry. Univ. of California Press.
وصلات خارجية
- Kiran Kedlaya, Geometry Unbound (a treatment using analytic geometry; PDF format, GFDL licensed)
- Articles to be expanded from March 2009
- All articles to be expanded
- Mathematics articles needing expert attention
- Miscellaneous articles needing expert attention
- Articles needing expert attention since December 2010
- Pages needing expert attention
- Articles to be expanded from June 2010
- Articles with hatnote templates targeting a nonexistent page
- CS1 errors: ISBN
- CS1 errors: format without URL
- اختراعات يونانية
- هندسة رياضية
- هندسة إقليدية
- هندسة ابتدائية