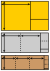
زاوية ذهبية

في الهندسة، الزاوية الذهبية Golden angle هي الزاوية التي نصنعها عندما نقسم محيط الدائرة إلى قطاع a و قطاع صغير b بحيث يتحقق :
The golden angle is then the angle subtended by the smaller arc of length b. It measures approximately 137.5077640500378546463487 ...° OEIS: A096627 or in radians 2.39996322972865332 ... OEIS: A131988.
The name comes from the golden angle's connection to the golden ratio φ; the exact value of the golden angle is
or
where the equivalences follow from well-known algebraic properties of the golden ratio.
As its sine and cosine are transcendental numbers, the golden angle cannot be constructed using a straightedge and compass.[1]
الاشتقاق
The golden ratio is equal to φ = a/b given the conditions above.
Let ƒ be the fraction of the circumference subtended by the golden angle, or equivalently, the golden angle divided by the angular measurement of the circle.
But since
it follows that
This is equivalent to saying that φ 2 golden angles can fit in a circle.
The fraction of a circle occupied by the golden angle is therefore
The golden angle g can therefore be numerically approximated in degrees as:
or in radians as :
الزاوية الذهبية في الطبيعة
The golden angle plays a significant role in the theory of phyllotaxis; for example, the golden angle is the angle separating the florets on a sunflower.[2] Analysis of the pattern shows that it is highly sensitive to the angle separating the individual primordia, with the Fibonacci angle giving the parastichy with optimal packing density.[3]
Mathematical modelling of a plausible physical mechanism for floret development has shown the pattern arising spontaneously from the solution of a nonlinear partial differential equation on a plane.[4][5]
انظر أيضاً
المراجع
- ^ Freitas, Pedro J. (2021-01-25). "The Golden Angle is not Constructible" (in الإنجليزية). arXiv:2101.10818v1. Bibcode:2021arXiv210110818F – via arXiv.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Jennifer Chu (2011-01-12). "Here comes the sun". MIT News. Retrieved 2016-04-22.
- ^ Ridley, J.N. (February 1982). "Packing efficiency in sunflower heads". Mathematical Biosciences (in الإنجليزية). 58 (1): 129–139. doi:10.1016/0025-5564(82)90056-6.
- ^ Pennybacker, Matthew; Newell, Alan C. (2013-06-13). "Phyllotaxis, Pushed Pattern-Forming Fronts, and Optimal Packing" (PDF). Physical Review Letters (in الإنجليزية). 110 (24): 248104. arXiv:1301.4190. Bibcode:2013PhRvL.110x8104P. doi:10.1103/PhysRevLett.110.248104. ISSN 0031-9007. PMID 25165965.
- ^ "Sunflowers and Fibonacci: Models of Efficiency". ThatsMaths (in الإنجليزية). 2014-06-05. Retrieved 2020-05-23.
- Vogel, H (1979). "A better way to construct the sunflower head". Mathematical Biosciences. 44 (3–4): 179–189. doi:10.1016/0025-5564(79)90080-4.
- Prusinkiewicz, Przemysław; Lindenmayer, Aristid (1990). The Algorithmic Beauty of Plants. Springer-Verlag. pp. 101–107. ISBN 978-0-387-97297-8.