تحليل حقيقي
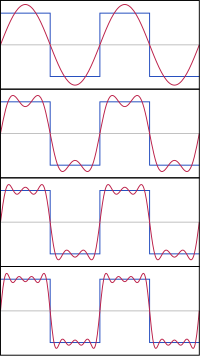
التحليل الحقيقي Real analysis هو أحد فروع الرياضيات التي تتعامل مع مجموعة الأعداد الحقيقية و الدوال المعرفة عليها . يمكن النظر إلى التحليل الحقيقي على انه نسخة مدققة من علم الحسبان (التفاضل و التكامل) يدرس مصطلحات مثل المتتاليات و نهاياتها ، الاستمرار في الدوال ، الاشتقاق الرياضي ، التكاملات الرياضية و اخيرا متتاليات الدوال . بالتالي يقدم التحليل الحقيقي نظرية متقنة حول فكرة الدوال العددية 'numerical function' ، كما يتضمن نظريات حديثة حول الدوال المعممة generalized function .
عادة ما يبدأ تقديم التحليل الحقيقي في النصوص الرياضية المتقدمة ببراهين بسيطة في نظرية المجموعات المبسطة naive set theory أو elementary set theory ، ثم تعريف واضح لمصطلح الدالة الرياضية ، ثم مقدمة للأعداد الطبيعية و تقنيات البرهان الهامة للاستقراء الرياضي mathematical induction .
من ثم تعمد النصوص المرجعية إلى تقديم الأعداد الحقيقية بشكل بدهي (أكسيوماتي) أو يتم تشكيلها من متتاليات كاوشي Cauchy sequence و حد ديديكايند Dedekind cut للأعداد المنطقة rational number . النتائج البدئية تشتق أولا ، اهمها خواص القيمة المطلقة absolute value ، مثل متراجحة المثلث triangle inequality و متراجحة برنولي Bernoulli's inequality .
مصطلح التقارب convergence يعتبر مفهوما مركزيا في التحليل الحقيقي ، فهو يقدم من خلال نهايات المتتاليات. يمكن اشتقاق عدة قوانين رياضية تحكم عملية الانتهاء ، و بالتالي يمكن حساب عدة نهايات . كما يدرس هنا أيضا المتسلسلات اللامنتهية Infinite series و هي عبارة عن نوع خاص م المتتاليات . من ثم تقدم متسلسلات القوى Power series القدرة على تعريف دوال مركزية متعددة مثل الدالة الأسية exponential function و الدوال المثلثية trigonometric function . من ثم يتم تقديم أنماط مهمة من المجموعات الجزئية مثل المجموعات المفتوحة open set و المجموعات المغلقة closed set ، المجموعات المضغوطة compact sets أو compact space مع خواصها المختلفة مثل مبرهنة بولزانو-فايرشتراس Bolzano-Weierstrass theorem و مبرهنة هايني-بوريل Heine-Borel theorem .
من أهم أقسام التحليل الحقيقي :
- مجموعة الأعداد حقيقية
- متتاليات حقيقية
- متسلسلات حقيقية
- نهاية الدوال الحقيقية
- دوال متصلة حقيقية
- اشتقاق الدوال حقيقية
- تكامل دوال حقيقية
نتائج هامة
Important results include the Bolzano–Weierstrass and Heine–Borel theorems, the intermediate value theorem and mean value theorem, Taylor's theorem, the fundamental theorem of calculus, the Arzelà-Ascoli theorem, the Stone-Weierstrass theorem, Fatou's lemma, and the monotone convergence and dominated convergence theorems.
اقرأ أيضا
- قائمة مواضيع التحليل الحقيقي
- Time-scale calculus – a unification of real analysis with calculus of finite differences
- Real multivariable function
- Real coordinate space
- تحليل مركب
الهامش
ببليوگرافيا
- Abbott, Stephen (2001). Understanding Analysis. Undergraduate Texts in Mathematics. New York: Springer-Verlag. ISBN 0-387-95060-5.
- Aliprantis, Charalambos D.; Burkinshaw, Owen (1998). Principles of real analysis (3rd ed.). Academic. ISBN 0-12-050257-7.
- Bartle, Robert G.; Sherbert, Donald R. (2011). Introduction to Real Analysis (4th ed.). New York: John Wiley and Sons. ISBN 978-0-471-43331-6.
- Bressoud, David (2007). A Radical Approach to Real Analysis. MAA. ISBN 978-0-88385-747-2.
- Browder, Andrew (1996). Mathematical Analysis: An Introduction. Undergraduate Texts in Mathematics. New York: Springer-Verlag. ISBN 0-387-94614-4.
- Carothers, Neal L. (2000). Real Analysis. Cambridge: Cambridge University Press. ISBN 978-0521497565.
- Dangello, Frank; Seyfried, Michael (1999). Introductory Real Analysis. Brooks Cole. ISBN 978-0-395-95933-6.
- Kolmogorov, A. N.; Fomin, S. V. (1975). Introductory Real Analysis. Translated by Richard A. Silverman. Dover Publications. ISBN 0486612260. Retrieved 2 April 2013.
- Rudin, Walter (1976). Principles of Mathematical Analysis. Walter Rudin Student Series in Advanced Mathematics (3rd ed.). New York: McGraw–Hill. ISBN 978-0-07-054235-8.
- Rudin, Walter (1987). Real and Complex Analysis (3rd ed.). New York: McGraw-Hill. ISBN 978-0-07-054234-1.
- Spivak, Michael (1994). Calculus (3rd ed.). Houston, Texas: Publish or Perish, Inc. ISBN 091409890X.
وصلات خارجية
- How We Got From There to Here: A Story of Real Analysis by Robert Rogers and Eugene Boman
- A First Course in Analysis by Donald Yau
- Analysis WebNotes by John Lindsay Orr
- Interactive Real Analysis by Bert G. Wachsmuth
- A First Analysis Course by John O'Connor
- Mathematical Analysis I by Elias Zakon
- Mathematical Analysis II by Elias Zakon
- Trench, William F. (2003). Introduction to Real Analysis (PDF). Prentice Hall. ISBN 978-0-13-045786-8.
- Earliest Known Uses of Some of the Words of Mathematics: Calculus & Analysis
- Basic Analysis: Introduction to Real Analysis by Jiri Lebl
- Topics in Real and Functional Analysis by Gerald Teschl, University of Vienna.