معادلة أرنيوس

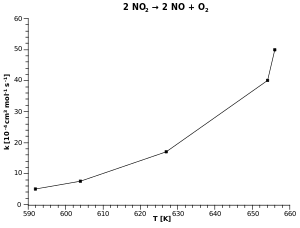
معادلة أرنيوس أو معادلة أرهنيوس في الكيمياء (بالإنجليزية: Arrhenius equation) هي معادلة مسماة باسم صاحبها العالم الكيميائي سڤانت أرنيوس وهي تصف المسيرة الزمنية للتفاعلات الكيميائية (حركية كيميائية). وتعطي تلك المعادلة مقادير ثابت معدل التفاعل خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} واعتماده على درجة الحرارة.

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=A\cdot e^\frac{-E_A}{R \cdot T}}

حيث :

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} معامل يسمى معامل التردد (أومعامل اصتدام الجزيئات) ،

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_A} : طاقة تنشيط (بوحدة : جول·مول^-1)،

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} : = 8,314 J·K^-1·mol^-1 ثابت الغازات العام

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} : درجة الحرارة (بوحدة :كلفن)،

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} : ثابت معدل التفاعل

ويلاحظ أن ادالة هنا دالة أسية للأساس الطبيعي e ، وأن كلا من البسط في الأس خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle {E_A}} والمقام خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle {R \cdot T}} لهما نفس الوحدة وهي جول/مول ، وبناءً على ذلك فالوحدات تمحو بعضها ويبقى الأس عددًا حقيقيًا ليست له وحدات (يقال عن ذلك تجانس الوحدات).

اعتبر أرنيوس معامل الاصطدام خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} ثابتا ، ولكن اتضح فيما أن المعادلة تقريبية ، وأن خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} نفسها تعتمد على درجة الحرارة طبقا للعلاقة :

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle A=u^*\cdot\sqrt{T}}

حيث u^* ثابت. ومنها نستنتج أن A تزيد مع الجزر التربيعي لدرجة الحرارة ، وتعمل بدورها هي الأخرى على تزايد سرعة التفاعل مع ارتفاع درجة الحرارة ، لكنه ارتفاعا بطيئا ، وان سرعة التفاعل تتحكم فيها درجة الحرارة بدرجة أشد من خلال الدالة الأسية.

إذن يمكننا كتابة المعادلة الأكثر دقة والتي تأخذ أيضا اعتماد المعامل A على درجة الحرارة كالآتي:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = B\cdot T^n\cdot e^{-\frac{E_A}{R \cdot T}}}

 عدد أرنيوس

In almost all practical cases, خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_a \gg RT} and k increases rapidly with T.

Mathematically, at very high temperatures so that خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_a \ll RT} , k levels off and approaches A as a limit, but this case does not occur under practical conditions.

تكتب "معادلة أرنيوس" كثيرا بالتعويض عن الأس في معادلته بعدد أرنيوس خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = \tfrac{E_A}{R \cdot T}} ، وهو عدد ليست له وحدة ، كما بيّنا أعلاه.

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle k=B\cdot T^n\cdot e^{-\gamma}}

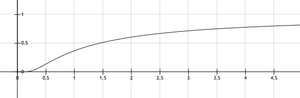
زيادة درجة الحرارة تزيد من المقام في الأس ، أي أن خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\gamma}} تقترب من الصفر بزيادة درجة الحرارة ، وتقترب الدالة الأسية من 1 ، وهو أكبر قيمة لها. بالتالي تكون k كبيرة ،أي يسير التفاعل سريعا مع ارتفاع درجة الحرارة. في نفس الوقت تتزايد k مع زيادة درجة الحرارة بالدرجة خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ T^n} ، ولكن المؤثر الأكبر يكمن في وجود درجة الحرارة في الأس في معادلة أرهينيوس.

 علاقة ثابت المعدل بطاقة گيبس الحرة

مع تقدم البحث أصبحنا الآن نكتب معادلة أرنيوس عن سير تفاعل كيميائي مع أخذ نظرية تحول الحالة التي صاغها يوجين ويگنر وزملاؤه عام 1930. وتكتب في أغلب الأحوال على الشكل :

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ k = \frac{k_BT}{h}e^{-\frac{\Delta G^\Dagger}{RT}}}

حيث :

ΔG^‡ طاقة جيبس الحرة للتنشيط،

k_B ثابت بولتزمان،

h ثابت پلانك.

نجد أن ثابت معامل التفاعل عبارة عن حاصل ضرب دالة أسية للاساس e في معامل خطي يعتمد على درجة الحرارة. ولكننا لا بد وأن نتذكر أن الطاقة الحرة هي الأخرى تعتمد على درجة الحرارة. ونقوم بتعيين الطاقة الحرة للتنشيط بأنها الفرق بين شطر المعادلة يدخل فيه الإنثالبي مطروحا منه شطر متعلق بالإنتروبية مضروبة في درجة الحرارة المطلقة. وإذا قمنا بأخذ جميع تلك المتغيرات في الحسبان فإننا نعود إلى معادلة أرنيوس التي تتكون من شطر أسي مضروبا في شطر يتغير بطيئا مع ارتفاع درجة الحرارة T.

 اقرأ أيضا

• مخطط أرنيوس
• معادلة إيرنگ
• معامل بولتسمان
• تفاعل كيميائي
• تفاعل ناشر للحرارة
• تفاعل يمتص الحرارة
• تفاعل الثرميت
• تفاعل أكسدة-اختزال
• اختزال
• نظرية تحول الحالة
• قاعدة ڤانت هوفت
• نظرية التصادم
• تفاعل نووي

 وصلات خارجية

• Carbon Dioxide solubility in Polyethylene – Using Arrhenius equation for calculating species solubility in polymers