نصف قطر الأرض
القطر الأرضي هو وحدة قياس تستخدم في القياسات الكبيرة، وهي تساوي قطر الأرض الذي يبلغ طوله 12,750 كيلومتر. وعلى سبيل المثال، يبلغ قطر الزهرة 12100 كلم أي 0.95 قطر أرضي.
مقدمة

فيزياء انبعاج الأرض
Rotation of a planet causes it to approximate an oblate ellipsoid/spheroid with a bulge at the equator and flattening at the North and South Poles, so that the equatorial radius a is larger than the polar radius b by approximately aq. The oblateness constant q is given by
where ω is the angular frequency, G is the gravitational constant, and M is the mass of the planet.[أ] For the Earth 1/q ≈ 289, which is close to the measured inverse flattening 1/f ≈ 298.257. Additionally, the bulge at the equator shows slow variations. The bulge had been decreasing, but since 1998 the bulge has increased, possibly due to redistribution of ocean mass via currents.[2]
The variation in density and crustal thickness causes gravity to vary across the surface and in time, so that the mean sea level differs from the ellipsoid. This difference is the geoid height, positive above or outside the ellipsoid, negative below or inside. The geoid height variation is under 110 m (360 ft) on Earth. The geoid height can change abruptly due to earthquakes (such as the Sumatra-Andaman earthquake) or reduction in ice masses (such as Greenland).[3]
Not all deformations originate within the Earth. The gravity of the Moon and Sun cause the Earth's surface at a given point to undulate by tenths of meters over a nearly 12-hour period (see Earth tide).
نصف القطر والأحوال المحلية
نصف القطر الثابت
نصف القطر الإستوائي
نصف القطر القطبي
أنصاف الأقطار المعتمدة على الموقع
Geocentric radius
The distance from the Earth's center to a point on the spheroid surface at geodetic latitude φ is:
where a and b are, respectively, the equatorial radius and the polar radius.
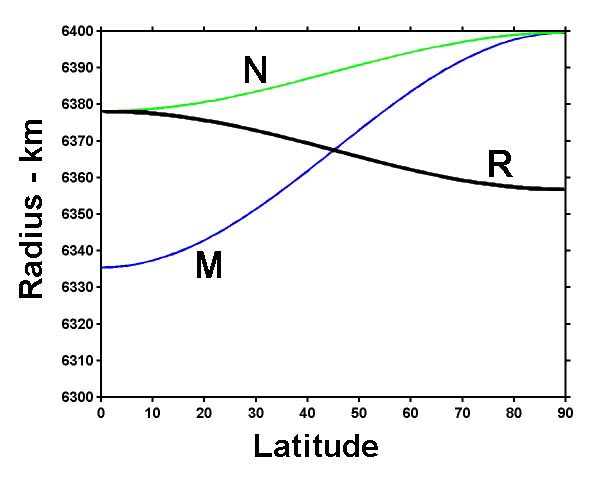
Notable geocentric radii
- Maximum: The summit of Chimborazo is 6،384.4 km (3،967.1 mi) from the Earth's center.
- Minimum: The floor of the Arctic Ocean is approximately 6،352.8 km (3،947.4 mi) from the Earth's center.[4]
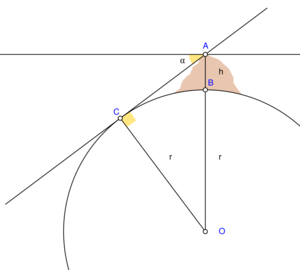
Radii of curvature
Principal sections
There are two principal radii of curvature: along the meridional and prime-vertical normal sections.
Meridional
In particular, the Earth's radius of curvature in the (north–south) meridian at φ is:
This is the radius that Eratosthenes measured.
The Earth's meridional radius of curvature at the equator equals the meridian's semi-latus rectum:
- b2/a = 6,335.439 km
The Earth's polar radius of curvature is:
- a2/b = 6,399.594 km
Directional
The Earth's radius of curvature along a course at an azimuth (measured clockwise from north) α at φ is derived from Euler's curvature formula as follows:[5]
Combinations
It is possible to combine the principal radii of curvature above in a non-directional manner.
انظر أيضاً
Notes
- ^ This follows from the International Astronomical Union definition rule (2): a planet assumes a shape due to hydrostatic equilibrium where gravity and centrifugal forces are nearly balanced.[1]
References
- ^ IAU 2006 General Assembly: Result of the IAU Resolution votes Archived 2006-11-07 at the Wayback Machine
- ^ Satellites Reveal A Mystery Of Large Change In Earth's Gravity Field , Aug. 1, 2002, Goddard Space Flight Center. Archived أبريل 28, 2010 at the Wayback Machine
- ^ NASA's Grace Finds Greenland Melting Faster, 'Sees' Sumatra Quake, December 20, 2005, Goddard Space Flight Center.
- ^ "Discover-TheWorld.com - Guam - POINTS OF INTEREST - Don't Miss - Mariana Trench". Guam.discover-theworld.com. 1960-01-23. Retrieved 2013-09-16.
- ^ خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةTorge
وصلات خارجية
- Merrifield, Michael R. (2010). " The Earth's Radius (and exoplanets)". Sixty Symbols. Brady Haran for the University of Nottingham.