قطع مخروطي
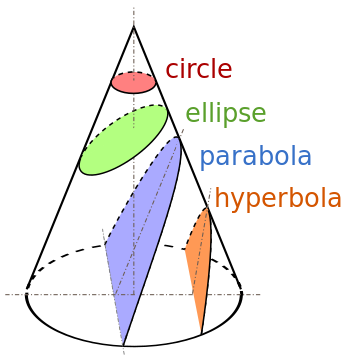
في الهندسة الوصفية القطعة المخروطية هو منحنى يُحصل عليها عند تقاطع مخروط بسطح لا يمر برأس و غير مماس له (التقاطع في هذه الحالات نقطة أو مستقيم). The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes called as a fourth type. دُرست القطع المخروطية منذ وقت طويل يعود إلى 200 قبل الميلاد، من قبل أبولونيوس من برجا.
The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic[1] to be the set of those points whose distances to some particular point, called a focus, and some particular line, called a directrix, are in a fixed ratio, called the eccentricity. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2; that is, as the set of points whose coordinates satisfy a quadratic equation in two variables which can be written in the form The geometric properties of the conic can be deduced from its equation.
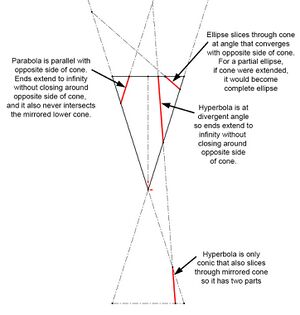
In the Euclidean plane, the three types of conic sections appear quite different, but share many properties. By extending the Euclidean plane to include a line at infinity, obtaining a projective plane, the apparent difference vanishes: the branches of a hyperbola meet in two points at infinity, making it a single closed curve; and the two ends of a parabola meet to make it a closed curve tangent to the line at infinity. Further extension, by expanding the real coordinates to admit complex coordinates, provides the means to see this unification algebraically.
الهندسة الإقليدية
في التحليل الرياضي القطوع المخروطية، هو المحل الهندسي لنقطة تتحرك بحيث تكون النسبة بين بعدها عن نقطة ثابتة وبعدها عن مستقيم ثابت تساوي نسبة ثابتة. تسمى هذه النسبة الإختلاف المركزي (Eccentricity)، كما تسمى النقطة الثابتة البؤرة (Focus)، أما المستقيم الثابت فيدعى الدليل (directrix).
حيث:
- P هي نقطة (x,y) تقع على القطع
- S البؤرة
- e معامل الاختلاف المركزي
- و m هي مسقط العمودي ل P على الدليل
إذا كان الإختلاف المركزي مساويا للوحدة (عدد الواحد الصحيح) سمي المنحنى قطعا مكافئا (Parabola)، وإذا كان الإختلاف المركزي أقل من الوحدة (الواحد الصحيح) سمي المنحنى قطعا ناقصا (Ellipse)، وإذا كان الإختلاف المركزي أكبر من الوحدة(الواحد) سمي المنحنى قطعا زائدا(Hyperbola).
وتسمى القطوع المكافئة والناقصة والزائدة بالقطوع المخروطية، لأنه يمكن أن تتولد نتيجة قطع السطح المخروطي بمستو في وضع معين.
المعادلة الجبرية
يمكن إعطاء معادلة القطع المخروطي بأشكال مختلفة منها:
- إذا كان الأختلاف المركزي يساوي هـ وكانت البؤرة عند نقطة الأصل (.،.) والدليل مستقيما عموديا على محور السينات يقطعه على بعد ف فإن معادلة القطع المخروطي تعطى بالمعادلة التالية:
(1 - هـ2)س2 + 2هـ2 ف س + ص2 = هـ2 ف
- معادلة من الدرجة الثانية في متغيرين س ، ص ويمكن كتابة هذه المعادلة على الصورة التالية:
أ س2 + 2ب س ص + جـ ص2 +2د س +2هـ ص + و = .
Pencil of conics
A (non-degenerate) conic is completely determined by five points in general position (no three collinear) in a plane and the system of conics which pass through a fixed set of four points (again in a plane and no three collinear) is called a pencil of conics.[2] The four common points are called the base points of the pencil. Through any point other than a base point, there passes a single conic of the pencil. This concept generalizes a pencil of circles.[3]
تقاطع مخروطين
The solutions to a system of two second degree equations in two variables may be viewed as the coordinates of the points of intersection of two generic conic sections. In particular two conics may possess none, two or four possibly coincident intersection points. An efficient method of locating these solutions exploits the homogeneous matrix representation of conic sections, i.e. a 3 × 3 symmetric matrix which depends on six parameters.
The procedure to locate the intersection points follows these steps, where the conics are represented by matrices:[4]
- given the two conics and , consider the pencil of conics given by their linear combination
- identify the homogeneous parameters which correspond to the degenerate conic of the pencil. This can be done by imposing the condition that and solving for and . These turn out to be the solutions of a third degree equation.
- given the degenerate conic , identify the two, possibly coincident, lines constituting it.
- intersect each identified line with either one of the two original conics; this step can be done efficiently using the dual conic representation of
- the points of intersection will represent the solutions to the initial equation system.
تعميمات
Conics may be defined over other fields (that is, in other pappian geometries). However, some care must be used when the field has characteristic 2, as some formulas can not be used. For example, the matrix representations used above require division by 2.
A generalization of a non-degenerate conic in a projective plane is an oval. An oval is a point set that has the following properties, which are held by conics: 1) any line intersects an oval in none, one or two points, 2) at any point of the oval there exists a unique tangent line.
Generalizing the focus properties of conics to the case where there are more than two foci produces sets called generalized conics.
The intersection of an elliptic cone with a sphere is a spherical conic, which shares many properties with planar conics.
في فروع أخرى للرياضيات
The classification into elliptic, parabolic, and hyperbolic is pervasive in mathematics, and often divides a field into sharply distinct subfields. The classification mostly arises due to the presence of a quadratic form (in two variables this corresponds to the associated discriminant), but can also correspond to eccentricity.
Quadratic form classifications:
- Quadratic forms
- Quadratic forms over the reals are classified by Sylvester's law of inertia, namely by their positive index, zero index, and negative index: a quadratic form in n variables can be converted to a diagonal form, as where the number of +1 coefficients, k, is the positive index, the number of −1 coefficients, ℓ, is the negative index, and the remaining variables are the zero index m, so In two variables the non-zero quadratic forms are classified as:
- – positive-definite (the negative is also included), corresponding to ellipses,
- – degenerate, corresponding to parabolas, and
- – indefinite, corresponding to hyperbolas.
- In two variables quadratic forms are classified by discriminant, analogously to conics, but in higher dimensions the more useful classification is as definite, (all positive or all negative), degenerate, (some zeros), or indefinite (mix of positive and negative but no zeros). This classification underlies many that follow.
- Curvature
- The Gaussian curvature of a surface describes the infinitesimal geometry, and may at each point be either positive – elliptic geometry, zero – Euclidean geometry (flat, parabola), or negative – hyperbolic geometry; infinitesimally, to second order the surface looks like the graph of (or 0), or . Indeed, by the uniformization theorem every surface can be taken to be globally (at every point) positively curved, flat, or negatively curved. In higher dimensions the Riemann curvature tensor is a more complicated object, but manifolds with constant sectional curvature are interesting objects of study, and have strikingly different properties, as discussed at sectional curvature.
- Second order PDEs
- Partial differential equations (PDEs) of second order are classified at each point as elliptic, parabolic, or hyperbolic, accordingly as their second order terms correspond to an elliptic, parabolic, or hyperbolic quadratic form. The behavior and theory of these different types of PDEs are strikingly different – representative examples is that the Poisson equation is elliptic, the heat equation is parabolic, and the wave equation is hyperbolic.
Eccentricity classifications include:
- Möbius transformations
- Real Möbius transformations (elements of PSL2(R) or its 2-fold cover, SL2(R)) are classified as elliptic, parabolic, or hyperbolic accordingly as their half-trace is or mirroring the classification by eccentricity.
- Variance-to-mean ratio
- The variance-to-mean ratio classifies several important families of discrete probability distributions: the constant distribution as circular (eccentricity 0), binomial distributions as elliptical, Poisson distributions as parabolic, and negative binomial distributions as hyperbolic. This is elaborated at cumulants of some discrete probability distributions.

انظر أيضاً
- Confocal conic sections
- Circumconic and inconic
- Director circle
- Elliptic coordinate system
- Equidistant set
- Parabolic coordinates
- Quadratic function
- Spherical conic
- قطع مكافيء Parabola.
- قطع ناقص Ellipse.
- قطع زائد Hyperbola.
مصادر
- معجم الرياضيات - تأليف لجنة من الخبراء من وزارة التربية والتعليم - عمان - طبعة مكتبة لبنان - ساحة رياض الصلح/ بيروت - 1980م.
ملاحظات
المراجع
- ^ Eves 1963
- ^ Faulkner 1952, pg. 64.
- ^ Berger, M., Geometry Revealed: A Jacob's Ladder to Modern Higher Geometry (Berlin/Heidelberg: Springer, 2010), p. 127.
- ^ Richter-Gebert 2011
ببليوجرافيا
- Akopyan, A.V.; Zaslavsky, A.A. (2007). Geometry of Conics. American Mathematical Society. ISBN 978-0-8218-4323-9.
- Artzy, Rafael (2008), Linear Geometry, Dover, ISBN 978-0-486-46627-9
- Boyer, Carl B. (2004), History of Analytic Geometry, Dover, ISBN 978-0-486-43832-0, https://books.google.com/books?id=2T4i5fXZbOYC
- Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1999), Geometry, Cambridge University Press, ISBN 978-0-521-59787-6, https://books.google.com/books?id=q49lhAzXTFEC
- Coxeter, H.S.M. (1964), Projective Geometry, Blaisdell, ISBN 9780387406237, https://books.google.com/books?id=gjAAI4FW0tsC
- Coxeter, H.S.M. (1993), The Real Projective Plane, Springer Science & Business Media
- Downs, J.W. (2003), Practical Conic Sections: The geometric properties of ellipses, parabolas and hyperbolas, Dover, ISBN 0-486-42876-1, https://books.google.com/books?id=PE7CAgAAQBAJ
- Eves, Howard (1963), A Survey of Geometry (Volume One), Boston: Allyn and Bacon
- Glaeser, Georg; Stachel, Hellmuth; Odehnal, Boris (2016), The Universe of Conics: From the ancient Greeks to 21st century developments, Berlin: Springer
- Hartmann, Erich, Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes, http://www.mathematik.tu-darmstadt.de/~ehartmann/circlegeom.pdf, retrieved on 20 September 2014 (PDF; 891 kB).
- Katz, Victor J. (1998), A History of Mathematics / An Introduction (2nd ed.), Addison Wesley Longman, ISBN 978-0-321-01618-8, https://archive.org/details/historyofmathema00katz
- Kendig, Keith (2005), Conics, The Mathematical Association of America, ISBN 978-0-88385-335-1
- Faulkner, T. E. (1952), Projective Geometry (2nd ed.), Edinburgh: Oliver and Boyd, ISBN 9780486154893, https://books.google.com/books?id=3TwCIg_O2yMC
- Merserve, Bruce E. (1983), Fundamental Concepts of Geometry, Dover, ISBN 0-486-63415-9, https://books.google.com/books?id=Y6jDAgAAQBAJ
- Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley
- Richter-Gebert, Jürgen (2011). Perspectives on Projective Geometry: A Guided Tour Through Real and Complex Geometry. Springer. ISBN 9783642172854.
- Samuel, Pierre (1988), Projective Geometry, Undergraduate Texts in Mathematics (Readings in Mathematics), New York: Springer-Verlag, ISBN 0-387-96752-4, https://archive.org/details/projectivegeomet0000samu
- Thomas, George B.; Finney, Ross L. (1979), Calculus and Analytic Geometry (fifth ed.), Addison-Wesley, p. 434, ISBN 0-201-07540-7
- Wilson, W.A.; Tracey, J.I. (1925), Analytic Geometry (Revised ed.), D.C. Heath and Company
وصلات خارجية