قطر زاوي
القطر الزاوي (إنگليزية: angular diameter) لجسم ما هو القطر المرئي للجسم من موقع معين مقاساً كزاوية. The angular diameter can alternately be thought of as the angle an eye or camera must rotate to look from one side of an apparent circle to the opposite side.
يستخدم القطر الزاوي في الفلك للتعبير عن قياس الأجسام في الفضاء.
الصيغ الرياضية
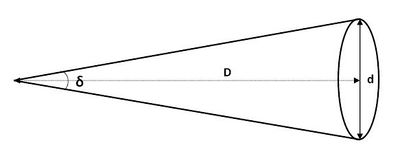
من الممكن حساب القطر الزاوي لشكل ما باستخدام العلاقة:
حيث القطر الزاوي و هي القطر المرئي والمسافة عن الجسم مقاسة بذات الواحدة عندما يكون أكبر بكثير من ، من الممكن تقريب قيمة بالعلاقة حيث قيمة الزاوية مقاسة بالراديان.
من أجل الأجسام الكروية التي قطرها الحقيقي يساوي يعطى القطر الزاوي بالعلاقة:
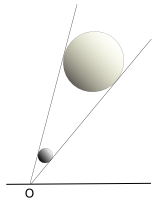
تقدير القطر الزاوي باستخدام كف مبسوطة
Estimates of angular diameter may be obtained by holding the hand at right angles to a fully extended arm, as shown in the figure.[1][2][3]
الاستخدام في الفلك
In astronomy the sizes of objects in the sky are often given in terms of their angular diameter as seen from Earth, rather than their actual sizes. Since these angular diameters are typically small, it is common to present them in arcseconds. An arcsecond is 1/3600th of one degree, and a radian is 180/ degrees, so one radian equals 3600*180/ arcseconds, which is about 206265 arcseconds. Therefore, the angular diameter of an object with physical diameter d at a distance D, expressed in arcseconds, is given by:[4]
- = (206265) d / D arcseconds.
The angular diameter of Earth's orbit around the Sun, from a distance of one parsec, is 1″ (one arcsecond).
The angular diameter of the Sun, from a distance of one light-year, is 0.03″, and that of the Earth 0.0003″. The angular diameter 0.03″ of the Sun given above is approximately the same as that of a person at a distance of the diameter of the Earth.[1]
This table shows the angular sizes of noteworthy celestial bodies as seen from the Earth:
| Celestial body | Angular diameter or size | Relative size |
|---|---|---|
| Sun | 31′31″ – 32′33″ | 30–31 times the maximum value for Venus (orange bar below) / 1891–1953″ |
| Moon | 29′20″ – 34′6″ | 28–32.5 times the maximum value for Venus (orange bar below) / 1760–2046″ |
| Helix Nebula | about 16′ by 28′ | |
| Spire in Eagle Nebula | 4′40″ | length is 280″ |
| Venus | 9.67″ – 63.00″ | |
| Jupiter | 29.80″ – 49.06″ | |
| Saturn | 14.50″ – 19.92″ | |
| Mars | 3.50″ – 25.08″ | |
| Mercury | 4.54″ – 13.02″ | |
| Uranus | 3.31″ – 4.04″ | |
| Neptune | 2.17″ – 2.36″ | |
| Ceres | 0.33″ – 0.84″ | |
| Vesta | 0.20″ – 0.64″ | |
| Pluto | 0.063″ – 0.115″ | |
| R Doradus | 0.052″ – 0.062″ | |
| Betelgeuse | 0.049″ – 0.060″ | |
| Eris | 0.034″ – 0.089″ | |
| Alphard | 0.00909″ | |
| Alpha Centauri A | 0.007″ | |
| Canopus | 0.006″ | |
| Sirius | 0.005936″ | |
| Altair | 0.003″ | |
| Deneb | 0.002″ | |
| Proxima Centauri | 0.001″ | |
| Alnitak | 0.0005″ | |
| A star like Alnitak at a distance where the Hubble space telescope would just be able to see it[5] | 6×10−10 arcsec |
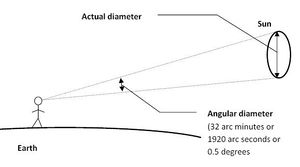
The table shows that the angular diameter of Sun, when seen from Earth is approximately 32 arcminutes (1920 arcseconds or 0.53 degrees), as illustrated above.
Thus the angular diameter of the Sun is about 250,000 times that of Sirius (Sirius has twice the diameter and its distance is 500,000 times as much; the Sun is 10^10 times as bright, corresponding to an angular diameter ratio of 10^5, so Sirius is roughly 6 times as bright per unit solid angle).
The angular diameter of the Sun is also about 250,000 times that of Alpha Centauri A (it has about the same diameter and the distance is 250,000 times as much; the Sun is 4×10^10 times as bright, corresponding to an angular diameter ratio of 200,000, so Alpha Centauri A is a little brighter per unit solid angle).
The angular diameter of the Sun is about the same as that of the Moon (the Sun's diameter is 400 times as large and its distance also; the Sun is 200,000 to 500,000 times as bright as the full Moon (figures vary), corresponding to an angular diameter ratio of 450 to 700, so a celestial body with a diameter of 2.5–4″ and the same brightness per unit solid angle would have the same brightness as the full Moon).
Even though Pluto is physically larger than Ceres, when viewed from Earth (e.g., through the Hubble Space Telescope) Ceres has a much larger apparent size.
While angular sizes measured in degrees are useful for larger patches of sky (in the constellation of Orion, for example, the three stars of the belt cover about 4.5 degrees of angular size), we need much finer units when talking about the angular size of galaxies, nebulae or other objects of the night sky.
Degrees, therefore, are subdivided as follows:
- 360 degrees (°) in a full circle
- 60 arc-minutes (′) in one degree
- 60 arc-seconds (″) in one arc-minute
To put this in perspective, the full moon viewed from Earth is about 1⁄2 degree, or 30 arc minutes (or 1800 arc-seconds). The Moon's motion across the sky can be measured in angular size: approximately 15 degrees every hour, or 15 arc-seconds per second. A one-mile-long line painted on the face of the Moon would appear to us to be about one arc-second in length.
In astronomy, it is typically difficult to directly measure the distance to an object. But the object may have a known physical size (perhaps it is similar to a closer object with known distance) and a measurable angular diameter. In that case, the angular diameter formula can be inverted to yield the Angular diameter distance to distant objects as
- .
In non-Euclidean space, such as our expanding universe, the angular diameter distance is only one of several definitions of distance, so that there can be different "distances" to the same object. See Distance measures (cosmology).
انظر أيضاً
- Angular diameter distance
- Angular resolution
- Solid angle
- Visual acuity
- Visual angle
- Visual Angle Illusion
- List of stars with resolved images
الهامش
- ^ https://dept.astro.lsa.umich.edu/ugactivities/Labs/coords/index.html
- ^ https://www.bartbusschots.ie/s/2013/06/08/photographing-satellites/
- ^ Wikiversity: Physics and Astronomy Labs/Angular size
- ^ Michael A. Seeds; Dana E. Backman (2010). Stars and Galaxies (7 ed.). Brooks Cole. p. 39. ISBN 978-0-538-73317-5.
- ^ 800 000 times smaller angular diameter than that of Alnitak as seen from Earth. Alnitak is a blue star so it gives off a lot of light for its size. If it were 800 000 times further away then it would be magnitude 31.5, at the limit of what Hubble can see.