المعرفة

عمر الكون

هذا المقال هو عن scientific estimates of the age of the universe. إذا كنت تريد religious and other non-scientific estimates، انظر Dating creation.

في علم الكون الفيزيائي، عمر الكون هو الوقت الكوني الوقت المنصرم منذ الانفجار العظيم. اليوم وقد اشتق علماء الفلك قياسين مختلفين للعصر:[1] وهناك قياس مبني على ملاحظة حالة الكون البعيد الناشئ، ونتيجة هذا القياس تقدر بحوالٍ 13.77 مليار عام (as of 2018[2])، 13.772±0.040 مليار عام طبقًا نموذج لامبدا-سي دي إم في 2018[2] والقياس التاني يعتمد على ملاحظة الكون المحلي الحديث الذي يشير إلى كون أصغر سنًا.[3][4][5] قلصت عدم اليقين للنوع الأول من القياس إلى 20 مليون عام. طبقًا لعدد من الدراسات والتي قدمت جميعها أرقامًا متشابهة للغاية بالنسبة للعمر. ويضم ذلك دراسات إشعاع الخلفية الكونية الميكروي التي قام بها مرصد پلانك الفضائي، ومسبار ولكنسون لقياس التباين الميكروي و وغيرهم من المجسات الفضائية. اعطت قياسات إشعاع الخلفية الكونية وقت التبريد للكون منذ الانفجار العظيم.[6] ويمكن استخدام قياس معدل توسع الكون لحساب العمر تقريبًا عن طريق الاستقراء إلى الوراء في الوقت. ويندرج نطاق التقدير أيضا تحت نطاق تقدير النجم الأقدم في الكون.


. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

التفسير

يصف نموذج لامبدا-سي دي إم تطور الكون منذ من حالته البدائية الموحدة والحارة والكثيفة إلى حالته الراهنة على مدى نحو 13.77 مليار سنة.[7] من الوقت الكوني. هذا النموذج مفهوم من الناحية النظرية ومدعوم بالكامل من جانب علم الفلك الرصدي عالي الجودة الحديث مثل مسبار ولكنسون لتباين الموجات الصغروية ، على النقيض تبقى نظريات أصل الحالة البدائية مجرد تخمينات. إذا قام المرء باستقراء نموذج نموذج لامبدا-سي دي إم إلى الوراء في أوائل حالته المفهومة جيدًا، سوف يصل بسرعة (في جزء صغير من الثانية) إلى التفرد. ويعرف ذلك باسم "التفرد المبدئي" أو "تفرد الانفجار العظيم". هذا التفرد غير مفهوم على أنه ذو أهمية مادية بالمعى المعتاد، ولكن من المناسب اقتباس أوقات تم قياسها "منذ الانفجار العظيم". على الرغم من أنها لا تتطابق مع وقت يمكن قياسه ماديًا. على سبيل المثال، "10−6 ثواني بعد الانفجار العظيم" تعتبر عصر محدد جيدًا في تطور الكون. وإذا اشار الشخص إلى نفس العصر على أنه 13.77 مليار سنة إلا 10 ثوان" سيفقد المعنى دقته لأن الفترة الزمنية الأخيرة الضئيلة يغلفهاعدم اليقين في السابقة.

على الرغم من أن الكون من الناحية النظرية قد يكون له تاريخ أطول، إلا أن الاتحاد الفلكي الدولي[8] يستخدم حاليًا مصطلح "عمر الكون" للاشارة إلى مدة تمدد نموذج لامبدا-سي دي إم، أو أو ما يعادل الوقت الذي انقضى منذ الانفجار العظيم في الكون المرصود حاليًا.


حدود الرصد

وبما أن الكون قد يكون على الأقل بعمر أقدم الأشياء به، هناك عدد من الموهناك عدد من الملاحظات التي تضع حدا أدنى لسن الكون؛[9][10] يتضمن ذلك حرارة الأقزام البيضاء التي تبرد تدريجيًا مع التقدم في السن، ومنعطف النسق الأساسي للنجم في تكتلات فالنجوم الأقل كتلة يقضون وقتًا أطول في التسلسل الرئيسي، تضع أقل النجوم تكتلًا التي تطورت بعيدًا عن التسلسل الرئيسي حددًا أدنى للعمر.)

Cosmological parameters

 
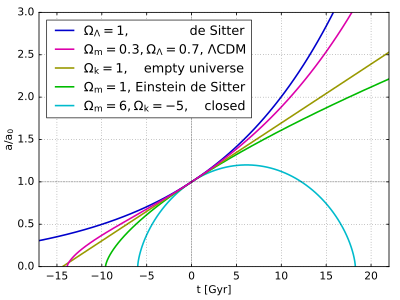
The age of the universe can be determined by measuring the Hubble constant today and extrapolating back in time with the observed value of density parameters (Ω). Before the discovery of dark energy, it was believed that the universe was matter-dominated (Einstein–de Sitter universe, green curve). Note that the de Sitter universe has infinite age, while the closed universe has the least age.
 
The value of the age correction factor, F, is shown as a function of two cosmological parameters: the current fractional matter density Ωm and cosmological constant density ΩΛ. The best-fit values of these parameters are shown by the box in the upper left; the matter-dominated universe is shown by the star in the lower right.

The problem of determining the age of the universe is closely tied to the problem of determining the values of the cosmological parameters. Today this is largely carried out in the context of the ΛCDM model, where the universe is assumed to contain normal (baryonic) matter, cold dark matter, radiation (including both photons and neutrinos), and a cosmological constant. The fractional contribution of each to the current energy density of the universe is given by the density parameters Ωm, Ωr, and ΩΛ. The full ΛCDM model is described by a number of other parameters, but for the purpose of computing its age these three, along with the Hubble parameter  , are the most important.

If one has accurate measurements of these parameters, then the age of the universe can be determined by using the Friedmann equation. This equation relates the rate of change in the scale factor a(t) to the matter content of the universe. Turning this relation around, we can calculate the change in time per change in scale factor and thus calculate the total age of the universe by integrating this formula. The age t0 is then given by an expression of the form

 

where   is the Hubble parameter and the function F depends only on the fractional contribution to the universe's energy content that comes from various components. The first observation that one can make from this formula is that it is the Hubble parameter that controls that age of the universe, with a correction arising from the matter and energy content. So a rough estimate of the age of the universe comes from the Hubble time, the inverse of the Hubble parameter. With a value for   around 69 km/s/Mpc, the Hubble time evaluates to   = 14.5 billion years.[11]

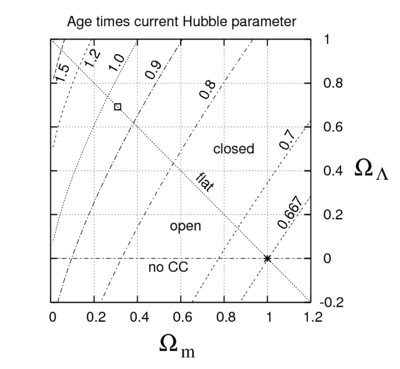
To get a more accurate number, the correction factor F must be computed. In general this must be done numerically, and the results for a range of cosmological parameter values are shown in the figure. For the Planck values (Ωm, ΩΛ) = (0.3086, 0.6914), shown by the box in the upper left corner of the figure, this correction factor is about F = 0.956. For a flat universe without any cosmological constant, shown by the star in the lower right corner, F = 2⁄3 is much smaller and thus the universe is younger for a fixed value of the Hubble parameter. To make this figure, Ωr is held constant (roughly equivalent to holding the CMB temperature constant) and the curvature density parameter is fixed by the value of the other three.

Apart from the Planck satellite, the Wilkinson Microwave Anisotropy Probe (WMAP) was instrumental in establishing an accurate age of the universe, though other measurements must be folded in to gain an accurate number. CMB measurements are very good at constraining the matter content Ωm[12] and curvature parameter Ωk.[13] It is not as sensitive to ΩΛ directly,[13] partly because the cosmological constant becomes important only at low redshift. The most accurate determinations of the Hubble parameter H0 come from Type Ia supernovae. Combining these measurements leads to the generally accepted value for the age of the universe quoted above.

The cosmological constant makes the universe "older" for fixed values of the other parameters. This is significant, since before the cosmological constant became generally accepted, the Big Bang model had difficulty explaining why globular clusters in the Milky Way appeared to be far older than the age of the universe as calculated from the Hubble parameter and a matter-only universe.[14][15] Introducing the cosmological constant allows the universe to be older than these clusters, as well as explaining other features that the matter-only cosmological model could not.[16]

WMAP

NASA's Wilkinson Microwave Anisotropy Probe (WMAP) project's nine-year data release in 2012 estimated the age of the universe to be (13.772±0.059)×109 years (13.772 billion years, with an uncertainty of plus or minus 59 million years).[6]

However, this age is based on the assumption that the project's underlying model is correct; other methods of estimating the age of the universe could give different ages. Assuming an extra background of relativistic particles, for example, can enlarge the error bars of the WMAP constraint by one order of magnitude.[17]

This measurement is made by using the location of the first acoustic peak in the microwave background power spectrum to determine the size of the decoupling surface (size of the universe at the time of recombination). The light travel time to this surface (depending on the geometry used) yields a reliable age for the universe. Assuming the validity of the models used to determine this age, the residual accuracy yields a margin of error near one percent.[18]

Planck

In 2015, the Planck Collaboration estimated the age of the universe to be 13.813±0.038 billion years, slightly higher but within the uncertainties of the earlier number derived from the WMAP data.[19]

In the table below, figures are within 68% confidence limits for the base ΛCDM model.

Legend:

Cosmological parameters from 2015 Planck results[19]
Parameter Symbol TT+lowP TT+lowP
+lensing		 TT+lowP
+lensing+ext		 TT,TE,EE+lowP TT,TE,EE+lowP
+lensing		 TT,TE,EE+lowP
+lensing+ext
Age of the universe
(Ga)		   13.813±0.038 13.799±0.038 13.796±0.029 13.813±0.026 13.807±0.026 13.799±0.021
Hubble constant
(km⁄Mpc⋅s)		   67.31±0.96 67.81±0.92 67.90±0.55 67.27±0.66 67.51±0.64 67.74±0.46

In 2018, the Planck Collaboration updated its estimate for the age of the universe to 13.772±0.040 billion years.[2]

Assumption of strong priors

Calculating the age of the universe is accurate only if the assumptions built into the models being used to estimate it are also accurate. This is referred to as strong priors and essentially involves stripping the potential errors in other parts of the model to render the accuracy of actual observational data directly into the concluded result. Although this is not a valid procedure in all contexts (as noted in the accompanying caveat: "based on the fact we have assumed the underlying model we used is correct"[بحاجة لمصدر]), the age given is thus accurate to the specified error (since this error represents the error in the instrument used to gather the raw data input into the model).

The age of the universe based on the best fit to Planck 2018 data alone is 13.772±0.040 billion years. This number represents an accurate "direct" measurement of the age of the universe (other methods typically involve Hubble's law and the age of the oldest stars in globular clusters, etc.). It is possible to use different methods for determining the same parameter (in this case – the age of the universe) and arrive at different answers with no overlap in the "errors". To best avoid the problem, it is common to show two sets of uncertainties; one related to the actual measurement and the other related to the systematic errors of the model being used.

An important component to the analysis of data used to determine the age of the universe (e.g. from Planck) therefore is to use a Bayesian statistical analysis, which normalizes the results based upon the priors (i.e. the model).[18] This quantifies any uncertainty in the accuracy of a measurement due to a particular model used.[20][21]


. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

History

المقالة الرئيسية: Cosmic age problem and Cosmic microwave background

In the 18th century, the concept that the age of the Earth was millions, if not billions, of years began to appear. However, most scientists throughout the 19th century and into the first decades of the 20th century presumed that the universe itself was Steady State and eternal, possibly with stars coming and going but no changes occurring at the largest scale known at the time.

The first scientific theories indicating that the age of the universe might be finite were the studies of thermodynamics, formalized in the mid-19th century. The concept of entropy dictates that if the universe (or any other closed system) were infinitely old, then everything inside would be at the same temperature, and thus there would be no stars and no life. No scientific explanation for this contradiction was put forth at the time.

In 1915 Albert Einstein published the theory of general relativity[22] and in 1917 constructed the first cosmological model based on his theory. In order to remain consistent with a steady state universe, Einstein added what was later called a cosmological constant to his equations. Einstein's model of a static universe was proved unstable by Arthur Eddington.

The first direct observational hint that the universe was not static but expanding came from the observations of 'recession velocities', mostly by Vesto Slipher, combined with distances to the 'nebulae' (galaxies) by Edwin Hubble in a work published in 1929.[23] Earlier in the 20th century, Hubble and others resolved individual stars within certain nebulae, thus determining that they were galaxies, similar to, but external to, our Milky Way Galaxy. In addition, these galaxies were very large and very far away. Spectra taken of these distant galaxies showed a red shift in their spectral lines presumably caused by the Doppler effect, thus indicating that these galaxies were moving away from the Earth. In addition, the farther away these galaxies seemed to be (the dimmer they appeared to us) the greater was their redshift, and thus the faster they seemed to be moving away. This was the first direct evidence that the universe is not static but expanding. The first estimate of the age of the universe came from the calculation of when all of the objects must have started speeding out from the same point. Hubble's initial value for the universe's age was very low, as the galaxies were assumed to be much closer than later observations found them to be.

The first reasonably accurate measurement of the rate of expansion of the universe, a numerical value now known as the Hubble constant, was made in 1958 by astronomer Allan Sandage.[24] His measured value for the Hubble constant came very close to the value range generally accepted today.

However Sandage, like Einstein, did not believe his own results at the time of discovery. His value for the age of the universeقالب:Elucidate was too short to reconcile with the 25-billion-year age estimated at that time for the oldest known stars. Sandage and other astronomers repeated these measurements numerous times, attempting to reduce the Hubble constant and thus increase the resulting age for the universe. Sandage even proposed new theories of cosmogony to explain this discrepancy. This issue was more or less resolved by improvements in the theoretical models used for estimating the ages of stars. As of 2013, using the latest models for stellar evolution, the estimated age of the oldest known star is 14.46±0.8 billion years.[25]

The discovery of microwave cosmic background radiation announced in 1965[26] finally brought an effective end to the remaining scientific uncertainty over the expanding universe. It was a chance result from work by two teams less than 60 miles apart. In 1964, Arno Penzias and Robert Wilson were trying to detect radio wave echoes with a supersensitive antenna. The antenna persistently detected a low, steady, mysterious noise in the microwave region that was evenly spread over the sky, and was present day and night. After testing, they became certain that the signal did not come from the Earth, the Sun, or our galaxy, but from outside our own galaxy, but could not explain it. At the same time another team, Robert H. Dicke, Jim Peebles, and David Wilkinson, were attempting to detect low level noise which might be left over from the Big Bang and could prove whether the Big Bang theory was correct. The two teams realized that the detected noise was in fact radiation left over from the Big Bang, and that this was strong evidence that the theory was correct. Since then, a great deal of other evidence has strengthened and confirmed this conclusion, and refined the estimated age of the universe to its current figure.

The space probes WMAP, launched in 2001, and Planck, launched in 2009, produced data that determines the Hubble constant and the age of the universe independent of galaxy distances, removing the largest source of error.[18]


. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

See also

References

  1. ^ European Space Agency (17 July 2018). "From an almost perfect Universe to the best of both worlds. Planck. (last paragraphs)". European Space Agency. Archived from the original on 13 April 2020.
  2. ^ أ ب ت Planck Collaboration (2020). "Planck 2018 results. VI. Cosmological parameters (See PDF, page 15, Table 2, Age/Gyr, last column)". Astronomy & Astrophysics. 641: A6. arXiv:1807.06209. doi:10.1051/0004-6361/201833910. S2CID 119335614.
  3. ^ Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; Bucciarelli, Beatrice; Lattanzi, Mario G.; MacKenty, John W.; Bowers, J. Bradley; Zheng, Weikang; Filippenko, Alexei V.; Huang, Caroline (2018-07-12). "Milky Way Cepheid Standards for Measuring Cosmic Distances and Application to Gaia DR2: Implications for the Hubble Constant". The Astrophysical Journal. 861 (2): 126. arXiv:1804.10655. Bibcode:2018ApJ...861..126R. doi:10.3847/1538-4357/aac82e. ISSN 1538-4357. S2CID 55643027.{{cite journal}}: CS1 maint: unflagged free DOI (link)
  4. ^ ESA/Planck Collaboration (17 July 2018). "Measurements of the Hubble constant". European Space Agency. Archived from the original on 7 October 2020. {{cite web}}: |archive-date= / |archive-url= timestamp mismatch; 6 أكتوبر 2020 suggested (help)
  5. ^ Freedman, Wendy L.; Madore, Barry F.; Hatt, Dylan; Hoyt, Taylor J.; Jang, In-Sung; Beaton, Rachael L.; Burns, Christopher R.; Lee, Myung Gyoon; Monson, Andrew J.; Neeley, Jillian R.; Phillips, Mark M. (2019-08-29). "The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch". The Astrophysical Journal. 882 (1): 34. arXiv:1907.05922. Bibcode:2019ApJ...882...34F. doi:10.3847/1538-4357/ab2f73. ISSN 1538-4357. S2CID 196623652.{{cite journal}}: CS1 maint: unflagged free DOI (link)
  6. ^ أ ب Bennett, C.L.; et al. (2013). "Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results". The Astrophysical Journal Supplement Series. 208 (2): 20. arXiv:1212.5225. Bibcode:2013ApJS..208...20B. doi:10.1088/0067-0049/208/2/20. S2CID 119271232.
  7. ^ "Cosmic Detectives". European Space Agency. 2 April 2013. Retrieved 2013-04-15.
  8. ^ Chang, K. (9 March 2008). "Gauging Age of Universe Becomes More Precise". The New York Times.
  9. ^ Chaboyer, Brian (1 December 1998). "The age of the universe". Physics Reports. 307 (1–4): 23–30. doi:10.1016/S0370-1573(98)00054-4.
  10. ^ Chaboyer, Brian (16 February 1996). "A Lower Limit on the Age of the Universe". Science. 271 (5251): 957–961. arXiv:astro-ph/9509115. doi:10.1126/science.271.5251.957.
  11. ^ Liddle, A. R. (2003). An Introduction to Modern Cosmology (2nd ed.). Wiley. p. 57. ISBN 978-0-470-84835-7.
  12. ^ Hu, W. "Animation: Matter Content Sensitivity. The matter-radiation ratio is raised while keeping all other parameters fixed". University of Chicago. Archived from the original on 23 February 2008. Retrieved 2008-02-23.
  13. ^ أ ب Hu, W. "Animation: Angular diameter distance scaling with curvature and lambda". University of Chicago. Archived from the original on 23 February 2008. Retrieved 2008-02-23.
  14. ^ "Globular Star Clusters". SEDS. 1 July 2011. Archived from the original on 24 February 2008. Retrieved 2013-07-19.
  15. ^ Iskander, E. (11 January 2006). "Independent age estimates". University of British Columbia. Archived from the original on 6 March 2008. Retrieved 2008-02-23.
  16. ^ Ostriker, J. P.; Steinhardt, P. J. (1995). "Cosmic Concordance". arXiv:astro-ph/9505066.
  17. ^ de Bernardis, F.; Melchiorri, A.; Verde, L.; Jimenez, R. (2008). "The Cosmic Neutrino Background and the Age of the Universe". Journal of Cosmology and Astroparticle Physics. 2008 (3): 20. arXiv:0707.4170. Bibcode:2008JCAP...03..020D. doi:10.1088/1475-7516/2008/03/020. S2CID 8896110.
  18. ^ أ ب ت Spergel, D. N.; et al. (2003). "First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters". The Astrophysical Journal Supplement Series. 148 (1): 175–194. arXiv:astro-ph/0302209. Bibcode:2003ApJS..148..175S. doi:10.1086/377226. S2CID 10794058.
  19. ^ أ ب Planck Collaboration (2016). "Planck 2015 results. XIII. Cosmological parameters (See PDF, page 32, Table 4, Age/Gyr, last column)". Astronomy & Astrophysics. 594: A13. arXiv:1502.01589. Bibcode:2016A&A...594A..13P. doi:10.1051/0004-6361/201525830. S2CID 119262962.
  20. ^ Loredo, T. J. (1992). "The Promise of Bayesian Inference for Astrophysics".: 275–297, Springer-Verlag. doi:10.1007/978-1-4613-9290-3_31. 
  21. ^ Colistete, R.; Fabris, J. C.; Concalves, S. V. B. (2005). "Bayesian Statistics and Parameter Constraints on the Generalized Chaplygin Gas Model Using SNe ia Data". International Journal of Modern Physics D. 14 (5): 775–796. arXiv:astro-ph/0409245. Bibcode:2005IJMPD..14..775C. doi:10.1142/S0218271805006729. S2CID 14184379.
  22. ^ Einstein, A. (1915). "Zur allgemeinen Relativitätstheorie". Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (in الألمانية): 778–786. Bibcode:1915SPAW.......778E.
  23. ^ Hubble, E. (1929). "A relation between distance and radial velocity among extra-galactic nebulae". Proceedings of the National Academy of Sciences. 15 (3): 168–173. Bibcode:1929PNAS...15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160.
  24. ^ Sandage, A. R. (1958). "Current Problems in the Extragalactic Distance Scale". The Astrophysical Journal. 127 (3): 513–526. Bibcode:1958ApJ...127..513S. doi:10.1086/146483.
  25. ^ Bond, H. E.; Nelan, E. P.; Vandenberg, D. A.; Schaefer, G. H.; Harmer, D. (2013). "HD 140283: A Star in the Solar Neighborhood that Formed Shortly After the Big Bang". The Astrophysical Journal. 765 (12): L12. arXiv:1302.3180. Bibcode:2013ApJ...765L..12B. doi:10.1088/2041-8205/765/1/L12. S2CID 119247629.
  26. ^ Penzias, A. A.; Wilson, R .W. (1965). "A Measurement of Excess Antenna Temperature at 4080 Mc/s". The Astrophysical Journal. 142: 419–421. Bibcode:1965ApJ...142..419P. doi:10.1086/148307.

External links

قالب:Cosmology topics

تمّ الاسترجاع من "https://www.marefa.org/w/index.php?title=عمر_الكون&oldid=2317523"