طريقة العناصر المتناهية
| معادلات تفاضلية |
|---|
 |
| Classification |
| الحل |
طريقة العناصر المنتهية (FEM) أو يطلق عليها أيضاً تحليل العناصر المنتهية هي طريقة تحليل عددي لإيجاد الحلول التقريبية للمعادلات التفاضلية الجزئية بالإضافة إلى الحلول التكاملية. يعتمد الحل إما على إلغاء المعادلات التفاضلية الجزئية نهائياً (في الحالات الساكنة) أو تقريب المعادلات التفاضلية الجزئية إلى معادلات تفاضلية نظامية والتي يكون من الممكن حلها باستخدام عدة طرق كطريقة أويلر أو رونگه-كوتا.
تطبيقات
هناك العديد من التطبيقات لطريقة العناصر المنتهية وأغلبها تتعلق بالهندسة الميكانيكية بشكل أو بآخر، حيث تستخدم هذه الطريقة ضمن عملية تصميم وتطوير المنتجات المختلفة. بعض برامج حساب العناصر المنتهية الحديثة تقوم بدراسة الحرارة، المغناطيسية الكهربائية، تدفق السوائل...الخ.
في دراسة تصميم المنشآت، تفيد طريقة العناصر المنتهية بشكل كبير في الحصول على متانة عالية للمنشآة بالإضافة إلى تخفيف وزنها وتقليص المواد اللازمة وبالتالي الكلفة اللازمة للإنشاء.
شرح طريقة العناصر المنتهية
سوف نستخدم مثالين بسيطين لشرح طريقة العناصر المنتهية، والتي من خلالها من الممكن استخلاص الطريقة العامة. في النقاش التالي، يجب على القارئ أن يكون متفهما لمبادئ علم الحسبان والجبر الخطي.
P1 هي مسألة أحادية البعد، معطاة على الشكل التالي:
حيث معلوم و هو تابع مجهول للمتحول ، و هو المشتق الثاني للتابع بالنسبة للمتحول .
المسألة ثنائية البعد البسيطة هي مسألة ديركلت وتعطى على الشكل التالي:
حيث هي منطقة مفتوحة متصلة في المستوي الثنائي البعد الذي تكون حدوده هي عبارة عن مضلع ذو شكل جميل. و و هي المشتقات الثانية للمتحولين و على الترتيب.
من الممكن حل المسألة أحادية البعد بحساب المشتق العكسي. لكن هذه الطريقة في حل مسألة القيمة الحدية BVP تصلح لحل المسائل أحادية البعد ولا يمكن تعميمها إلى مسائل ذات أبعاد أعلى أو مثال لها الشكل ولهذا السبب كان من الضروري تطوير طريقة العناصر المنتهية، بدءاً من البعد الأحادي وتعميمها على الأبعاد الأعلى.
الشرح هنا سوف يتم على مرحلتين والتي تعكس المرحلتين الأساسيتين الواجب تطبيقهما لحل مسألة القيمة الحدية BVP باستخدام طريقة العناصر المنتهية:
- الخطوة الأولى: تبسيط مسألة القيمة الحدية BVP إلى شكل بسيط تنتفي معه الحاجة إلى استخدام الحاسب للحل، بل يكون من الممكن حلها يدوياً باستخدام الورقة والقلم.
- الخطوة الثانية: هي التقطيع، حيث يتم تجزئة الشكل إلى عناصر منتهية وحل كل عنصر على حدة.
بعد هذه الخطوة سيكون لدينا صيغة متكاملة لحل مسائل ذات درجات عالية لكن يجب أن تكون خطية والتي حلولها ستكون حلاً تقريبياً لمسألة القيمة الحدية. ومن ثم يتم برمجة هذه الطريقة على الحاسوب.
الصيغة المتحولية
الخطوة الأولى هو تحويل P1 و P2 إلى مكافئاتها المتحولية. إذا كان هو حل لـ P1، عندها من أجل أي دالة متصلة يحقق شروط الانتقال الحدي، مثلاً: عند و ، يكون لدينا
(1)
وبشكل معاكس، من أجل قيمة معطاة لـ فإن (1) تكون محققة من أجل أي دالة متصلة وعندها من الممكن أن يبرهن أن ستكون حلاً لـ P1 (برهان هذا ليس بالأمر السهل وهو يعتمد على فضاء سوبوليف).
وباستخدام التكامل بالأجزاء على يمين المعادلة (1) سنحصل على مايلي:
(2)
حيث تم افتراض أن .
برهان يظهر وجود حل وحيد
من الممكن اعتبار أن هو عبارة عن تابع مستمر مطلق للثنائية بحيث أن عند و (انظر فضاء سوبوليف). مثل هذه التوابع تكون ضعيفة (قابلة للاشتقاق مرة واحدة) وتكشف عن الخريطة الخطية الثنائية المتناظرة ومن ثم تعرف جداء داخلي الذي يحول إلى فضاء هلبرت. ومن ناحية أخرى، فإن الطرف الأيسر هو أيضاً جداء داخلي، ولكن هذه المرة على الفضاء Lp . وتطبيق لمبرهنة تمثيل رايسز على فضاءات هلبرت يظهر أنه يوجد حل وحيد يحل (2) وبالتالي يحل المسألة P1.
الصيغة المتحولية لـ P2
إذا تم التكامل بالأجزاء باستخدام مبرهنة غرين حيث نجد أنه إذا كان هو حل لـ P2، فإنه من أجل أي يكون
حيث تحقق التدرج وترمز إلى الجداء الداخلي في المستوي ثنائي البعد.
التقطيع
الفكرة الأساسية في طريقة العناصر المنتهية هو استبدال المسألة الخطية ذات الأبعاد اللانهائية: أوجد قيمة بحيث أن
بصيغة بعدية منتهية:
- (3) أوجد such that
حيث هو فضاء جزئي خطي ذو عدد أبعاد منته من . هناك العديد من الخيارات لـ . لكن في طريقة العناصر المنتهية نعتبر على أنها فضاء للأجزاء الخطية للتابع.
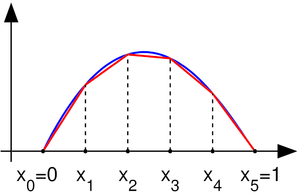
في المسألة P1، نأخذ المقطع باختيار قيم من ونعرف على الشكل:
حيث نعرف و . لاحظ أن التوابع في هي توابع غير قابلة للاشتقاق بالاعتماد على التعريف المبدئي للحسبان. إذا كان فإن المشتق يكون عادة غير معرف عند أي , . لكن يوجد مشتق عند كل قيمة للمتحول ومن الممكن استخدام هذا المشتق لغرض التكامل بالأجزاء.
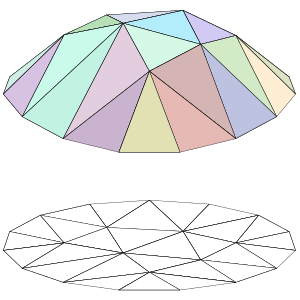
من أجل المسألة P2 نحتاج أن تكون عبارة عن مجموعة من التوابع من . في الشكل الموضح على اليسار، يظهر تثليث مضلعي لمنطقة مضلعية من 15 ضلع في المستوي (في الأسفل)، والتابع الخطى المجزأ (ملوناً، في الأعلى) لهذا المضلع الذي يكون خطياً على كل مثلث من التثليث. حيث أن الفضاء سيحتوي على توابع تكون خطية على كل مثلث من التثليث المختار.
تظهر مكتوبة على الشكل في بعض المراجع، وذلك بسبب أنه يوجد هدف في الحصول على حلول أدق وأدق للمسألة المتقطعة (3) الذي سيكون إلى حد ما سيؤدي إلى حد المسألة الأصلية في إيجاد القيم الحدية للمسألة P2. يتم عنونة التثليث باستخدام معامل ذو قيمة حقيقية والذي يكون ذو قيمة صغيرة. سوف يتم ربط هذا المعامل بحجم أكبر مثلث وسطي الحجم في التثليث. وعندما نزيد تجزئة التثليث فإن فضاء التقطيع الخطي يجب أن يتغير مع كما يوضح الترميز .
انظر أيضاً
- Applied element method
- Boundary element method
- Computer experiment
- Direct stiffness method
- Discontinuity layout optimization
- Discrete element method
- Finite element machine
- Finite element method in structural mechanics
- Finite volume method for unsteady flow
- Interval finite element
- Isogeometric analysis
- Lattice Boltzmann methods
- List of finite element software packages
- Movable cellular automaton
- Multidisciplinary design optimization
- Multiphysics
- Patch test
- Rayleigh–Ritz method
- Weakened weak form
- الدخاخني
الهامش
للاستزادة
- G. Allaire and A. Craig: Numerical Analysis and Optimization:An Introduction to Mathematical Modelling and Numerical Simulation
- K. J. Bathe : Numerical methods in finite element analysis, Prentice-Hall (1976).
- J. Chaskalovic, Finite Elements Methods for Engineering Sciences, Springer Verlag, (2008).
- O. C. Zienkiewicz, R. L. Taylor, J. Z. Zhu : The Finite Element Method: Its Basis and Fundamentals, Butterworth-Heinemann, (2005).
وصلات خارجية
- IFER Internet Finite Element Resources - Describes and provides access to finite element analysis software via the Internet.
- MIT Open Course-ware on Linear finite element method (With video lectures)
- NAFEMS—The International Association for the Engineering Analysis Community
- Finite Element Analysis Resources- Finite Element news, articles and tips
- Finite-element Methods for Electromagnetics - free 320-page text
- Finite Element Books- books bibliography
- Mathematics of the Finite Element Method
- Finite Element Methods for Partial Differential Equations - Lecture notes by Endre Süli
- Electromagnetic Modeling web site at Clemson University (includes list of currently available software)







































![{\displaystyle {\begin{matrix}V=\{v:[0,1]\rightarrow {\mathbb {R}}\;:v{\mbox{ is continuous, }}v|_{[x_{k},x_{k+1}]}{\mbox{ is linear for }}\\k=0,...,n{\mbox{, and }}v(0)=v(1)=0\}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd6687aed4c4deccc2124114a3cbb16b7453c374)