صيغة براهماگوپتا

في الهندسة الرياضية، تقوم صيغة براهماگوپتا بإيجاد مساحة أي رباعي أضلاع بواسطة طول أضلاعه وقياس بعض زواياه.

بشكلها الأكثر شيوعاً تقوم المعادلة بحساب معادلة رباعي الأضلاع المحصور ضمن دائرة (رباعي دائري).

الصيغة البسيطة

أبسط صيغة لصيغة براهماگوپتا هي الصيغة التي تعطى في الرباعي الدائري الذي أطوال أضلاعهa, b, c, d على الشكل التالي:

{\sqrt {(s-a)(s-b)(s-c)(s-d)}}

حيث s تعطى بالعلاقة: $s={\frac {a+b+c+d}{2}}.$

s-a={\frac {-a+b+c+d}{2}}

s-b={\frac {a-b+c+d}{2}}

s-c={\frac {a+b-c+d}{2}}

s-d={\frac {a+b+c-d}{2}}

وهي تعميم لمعادلة هيرون لحساب مساحة المثلث.

K={\frac {\sqrt {(a^{2}+b^{2}+c^{2}+d^{2})^{2}+8abcd-2(a^{4}+b^{4}+c^{4}+d^{4})}}{4}}\cdot

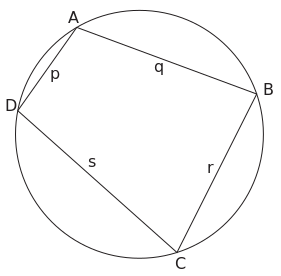
اثبات صيغة براهماگوپتا

مخطط مرجعي

Here we use the notations in the figure to the right. Area of the cyclic quadrilateral = Area of $\triangle ADB$ + Area of $\triangle BDC$

={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin C.

But since $ABCD$ is a cyclic quadrilateral, $\angle DAB=180^{\circ }-\angle DCB.$ Hence $\sin A=\sin C.$ Therefore

{\mbox{Area}}={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin A

({\mbox{Area}})^{2}={\frac {1}{4}}\sin ^{2}A(pq+rs)^{2}

4({\mbox{Area}})^{2}=(1-\cos ^{2}A)(pq+rs)^{2}=(pq+rs)^{2}-\cos ^{2}A(pq+rs)^{2}.\,

Solving for common side DB, in $\triangle$ ADB and $\triangle$ BDC, the law of cosines gives

p^{2}+q^{2}-2pq\cos A=r^{2}+s^{2}-2rs\cos C.\,

Substituting $\cos C=-\cos A$ (since angles $A$ and $C$ are supplementary) and rearranging, we have

2\cos A(pq+rs)=p^{2}+q^{2}-r^{2}-s^{2}.\,

Substituting this in the equation for the area,

4({\mbox{Area}})^{2}=(pq+rs)^{2}-{\frac {1}{4}}(p^{2}+q^{2}-r^{2}-s^{2})^{2}

16({\mbox{Area}})^{2}=4(pq+rs)^{2}-(p^{2}+q^{2}-r^{2}-s^{2})^{2},\,

which is of the form $a^{2}-b^{2}=(a-b)(a+b)$ and hence can be written as

(2(pq+rs)-p^{2}-q^{2}+r^{2}+s^{2})(2(pq+rs)+p^{2}+q^{2}-r^{2}-s^{2})\,

which, regrouping, is of the form $(c^{2}-d^{2})(e^{2}-f^{2})$

=((r+s)^{2}-(p-q)^{2})((p+q)^{2}-(r-s)^{2})\,

hence yielding four linear factors: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle (c-d)(c+d)(e-f)(e+f)}