سدنيون
| Sedenions | |
|---|---|
| الرمز | |
| Type | جبر غير تجميعي |
| الوحدات | e0...e15 |
| المحايد الضربي | e0 |
| الخصائص الرئيسية | تجميع القوى توزيعية |
| الأنظمة الشائعة | |
في الجبر التجريدي، السـِدِنيون Sedenion يشكل 16 بعداً جبرياً فوق الأعداد الحقيقية. يرمز لمجموعة السدنيون بالرمز . يعرف حالياً نوعان من السيدينيون:
- سيدينيون تم الحصول عليه من إنشاء كايلي-ديكسون
- سيدينيون مخروطي (ذو 16 بعداً جبرياً).
الحساب
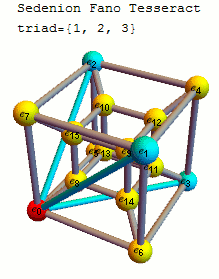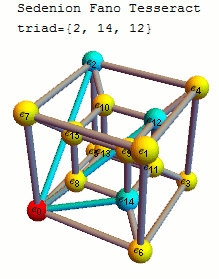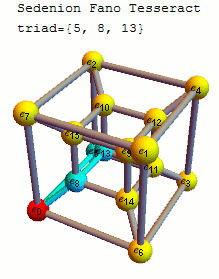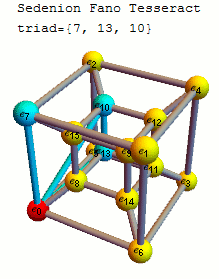
بشكل مشابه للأوكتونيون، فإن عملية ضرب السدنيون هي عملية غير تبديلية وغير تجميعية. ولكنه يمتلك خاصية تجميع القوى.
كل سدنيون هو عبارة عن تركيب خطي لعناصره وهي: 1, e1, e2, e3, e4, e5, e6, e7, e8, e9, e10, e11, e12, e13, e14 and e15 والتي هي أسس الفضاء الشعاعي للسدنيون.
يعطى جدول ضرب عناصر السدنيون الستة عشرة على الشكل التالي:
Like octonions, multiplication of sedenions is neither commutative nor associative. But in contrast to the octonions, the sedenions do not even have the property of being alternative. They do, however, have the property of power associativity, which can be stated as that, for any element x of , the power is well defined. They are also flexible.
Every sedenion is a linear combination of the unit sedenions , , , , ...,, which form a basis of the vector space of sedenions. Every sedenion can be represented in the form
- .
Addition and subtraction are defined by the addition and subtraction of corresponding coefficients and multiplication is distributive over addition.
Like other algebras based on the Cayley–Dickson construction, the sedenions contain the algebra they were constructed from. So, they contain the octonions (generated by to in the table below), and therefore also the quaternions (generated by to ), complex numbers (generated by and ) and reals (generated by ).
The sedenions have a multiplicative identity element and multiplicative inverses but they are not a division algebra because they have zero divisors. This means that two non-zero sedenions can be multiplied to obtain zero: an example is ( + )( − ). All hypercomplex number systems after sedenions that are based on the Cayley–Dickson construction contain zero divisors.
جدول ضرب السدنيونات هو التالي:
جدول الضرب
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sedenion properties
From the above table, we can see that:
Anti-associative
The sedenions are not fully anti-associative. Choose any four generators, and . The following 5-cycle shows that at least one of these relations must associate.
In particular, in the table above, using and the last expression associates.
Quaternionic subalgebras
The 35 triads that make up this specific sedenion multiplication table with the 7 triads of the octonions used in creating the sedenion through the Cayley–Dickson construction shown in bold:
The binary representations of the indices of these triples xor to 0.
{{1, 2, 3}, {1, 4, 5}, {1, 7, 6}, {1, 8, 9}, {1, 11, 10}, {1, 13, 12}, {1, 14, 15},
{2, 4, 6}, {2, 5, 7}, {2, 8, 10}, {2, 9, 11}, {2, 14, 12}, {2, 15, 13}, {3, 4, 7},
{3, 6, 5}, {3, 8, 11}, {3, 10, 9}, {3, 13, 14}, {3, 15, 12}, {4, 8, 12}, {4, 9, 13},
{4, 10, 14}, {4, 11, 15}, {5, 8, 13}, {5, 10, 15}, {5, 12, 9}, {5, 14, 11}, {6, 8, 14},
{6, 11, 13}, {6, 12, 10}, {6, 15, 9}, {7, 8, 15}, {7, 9, 14}, {7, 12, 11}, {7, 13, 10}}
The list of 84 sets of zero divisors {, , , }, where ( + )( + )=0:
التطبيقات
Moreno (1998) showed that the space of pairs of norm-one sedenions that multiply to zero is homeomorphic to the compact form of the exceptional Lie group G2. (Note that in his paper, a "zero divisor" means a pair of elements that multiply to zero.)
انظر أيضاً
الهامش
المراجع
- Imaeda, K.; Imaeda, M. (2000), "Sedenions: algebra and analysis", Applied Mathematics and Computation 115 (2): 77–88, doi:
- Baez, John C. (2002). "The Octonions". Bulletin of the American Mathematical Society. New Series. 39 (2): 145–205. arXiv:math/0105155. Bibcode:1994BAMaS..30..205W. doi:10.1090/S0273-0979-01-00934-X. MR 1886087.
{{cite journal}}: Invalid|ref=harv(help) - Kinyon, M.K.; Phillips, J.D.; Vojtěchovský, P. (2007). "C-loops: Extensions and constructions". Journal of Algebra and Its Applications. 6 (1): 1–20. arXiv:math/0412390. CiteSeerX 10.1.1.240.6208. doi:10.1142/S0219498807001990.
- Kivunge, Benard M.; Smith, Jonathan D. H (2004). "Subloops of sedenions" (PDF). Comment. Math. Univ. Carolinae. 45 (2): 295–302.
- Moreno, Guillermo (1998), "The zero divisors of the Cayley–Dickson algebras over the real numbers", Bol. Soc. Mat. Mexicana, Series 3 4 (1): 13–28, Bibcode: 1997q.alg....10013G
- Smith, Jonathan D. H. (1995), "A left loop on the 15-sphere", Journal of Algebra 176 (1): 128–138, doi:














































