سرعة الصوت
| قياسات الصوت | |
|---|---|
السمات | الرموز |
| ضغط الصوت | p, SPL,LPA |
| سرعة الجسيم | v, SVL |
| إزاحة الجسيم | δ |
| شدة الصوت | I, SIL |
| قوة الصوت | P, SWL, LWA |
| طاقة الصوت | W |
| كثافة طاقة الصوت | w |
| التعرض الصوتي | E, SEL |
| المعاوقة الصوتية | Z |
| التردد الصوتي | AF |
| فقدان الإرسال | TL |
سرعة الصوت، تعتمد سرعة الصوت على الوسط الذي ينتقل خلاله الصوت. وخصائص الوسط التي تحدد سرعة الصوت هي الكثافة وقابلية الانضغاط. والكثافة هي مقدار الكتلة الموجودة في وحدة الحجم من المادة. وتقيس قابلية الانضغاط مدى سهولة كبس المادة في حيز ضيق. وكلما زادت الكثافة وزادت قابلية الانضغاط، قلت سرعة الصوت.
تكون السوائل والأجسام الصلبة بصفة عامة أكثر كثافة من الهواء، ولكنها أيضًا أقل من الهواء بكثير في قابلية الانضغاط، ولذلك، فإن الصوت ينتقل بسرعة أكبر خلال السوائل والأجسام الصلبة. ولذلك نجد مثلاً أن سرعة الصوت في الماء نحو أربعة أمثال سرعته في الهواء، وسرعته في الفولاذ نحو 15 مرة مقدار سرعته في الهواء. وتقاس سرعة الصوت في الهواء عادة عند مستوى سطح البحر، وعند 15°م من الحرارة. وعند هذه الدرجة، ينتقل الصوت بسرعة 340 م/ث. ولكن سرعة الصوت تزداد بزيادة درجة الحرارة. فسرعة الصوت في الهواء، على سبيل المثال، 386 م/ث عند درجة الحرارة 100°م. تكون السوائل والأجسام الصلبة بصفة عامة أكثر كثافة من الهواء، ولكنها أيضًا أقل من الهواء بكثير في قابلية الانضغاط، ولذلك، فإن الصوت ينتقل بسرعة أكبر خلال السوائل والأجسام الصلبة. ولذلك نجد مثلاً أن سرعة الصوت في الماء نحو أربعة أمثال سرعته في الهواء، وسرعته في الفولاذ نحو 15 مرة مقدار سرعته في الهواء. وتقاس سرعة الصوت في الهواء عادة عند مستوى سطح البحر، وعند 15°م من الحرارة. وعند هذه الدرجة، ينتقل الصوت بسرعة 340 م/ث. ولكن سرعة الصوت تزداد بزيادة درجة الحرارة. فسرعة الصوت في الهواء، على سبيل المثال، 386 م/ث عند درجة الحرارة 100°م.
سرعة الصوت أقل بكثير من سرعة الضوء. يتحرك الضوء في الفراغ بسرعة 299,792 كم/ث، أي بنحو مليون مرة مقدار سرعة الصوت. ونتيجة لذلك، نرى وميض البرق أثناء العواصف، قبل أن نسمع صوت الرعد. وإذا راقبت نجارًا يطرق بالمطرقة من مسافة بعيدة، فإنك سترى المطرقة تطرق الخشب قبل أن تسمع صوتها.
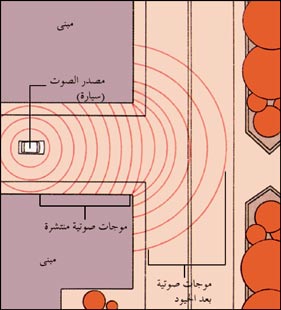
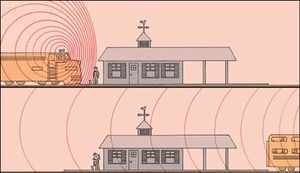
ولعلك لاحظت أن طبقة صوت صفارة القطار تبدو أعلى والقطار يقترب، وتبدو أقل بعد أن يمر القطار ويبتعد. تنتقل موجات الصوت التي تحدثها الصفارة بسرعة ثابتة في الهواء، بغض النظر عن سرعة القطار. ولكن، بينما يقترب القطار، فإن كل موجة تالية تحدثها الصفارة تقطع مسافة أقصر إلى آذاننا. ولذلك فإن الموجات تصل بمعدل أكبر، أي بتردد أكبر، وهنا تبدو طبقة الصوت أعلى. وعندما يبتعد القطار، فإن كل موجة تالية تقطع مسافة أطول إلى الأذن، فتصل الموجات بمعدل أقل، أي بتردد أقل، وتبدو طبقة الصوت أقل. ويسمى هذا التغير الظاهري في طبقة الصوت، الذي تحدثه الأجسام المتحركة تأثير دوبلر. ولا يتغير عمق الصوت بالنسبة لمستمع في القطار.
وتطير الطائرات النفاثة أحيانًا بسرعات تفوق سرعة الصوت. وتنتج الطائرة ذات السرعة التي تفوق سرعة الصوت موجات صدمية، وهي اضطرابات ضغط قوية تنشأ وتتراكم حول الطائرة. ويسمع الناس على الأرض ضجيجًا عاليًا، يُعرف باسم الفرقعة الصوتية (دوي اختراق حاجز الصوت)، عندما تعبر فوقهم موجات صدمية من الطائرة. انظر: الديناميكا الهوائية.
التاريخ
تضمن كتاب إسحاق نيوتن، في عام 1687، المبادئ حساب سرعة الصوت في الهواء بأنها 298 م/ث. وهي أقل من الرقم الحقيقي بنحو 15%.[1] ويرجع الاختلاف في المقام الأول إلى إهمال التأثير (غير المعروف آنذاك) لدرجات الحرارة سريعة التقلب في الموجة الصوتية (بالمصطلحات الحديثة، يُعد انضغاط الموجة الصوتية وتمدد الهواء عملية ثابتة الحرارة، وليست عملية ذات درجة حرارة متساوية). هذا الخطأ صححه لاحقاً لاپلاس.[2]
خلال القرن السابع عشر ، كانت هناك عدة محاولات لقياس سرعة الصوت بدقة ، بما في ذلك محاولات ماران مرسن في 1630 (1,380 قدم پاريسي في الثانية)، وپيير گاسندي في 1635 (1,473 قدم پاريسي في الثانية) و روبرت بويل (1,125 قدم پاريسي في الثانية).[3] وفي 1709، نشر القس وليام درم، القيـِّم في أپمنستر، قياساً أكثر دقة لسرعة الصوت، بقيمة 1,072 قدم پاريسي في الثانية.[3] (The القدم الپاريسي كان 325 مم. وهو أطول من "القدم الدولي" القياسي، شائع الاستخدام اليوم، الذي عـُرِّف رسمياً في 1959 بأنه 304.8 مم، مما يجعل سرعة الصوت عند درجة حرارة 20 °C (68 °F) 1,055 قدم پاريسي في الثانية).
استخدم درَم تلسكوپاً من برج كنيسة القديس لورنس، أپمنستر لرصد وميض بندقية بعيدة يتم اطلاقها، ثم قاس الوقت حتى سمع صوت الرصاص باستخدام بندول نصف ثانية. تم إجراء قياسات من طلقات نارية من عدد من المعالم المحلية ، بما في ذلك كنيسة شمال أوكندون. كانت المسافة معروفة بـ التثليث ، وبالتالي تم حساب السرعة التي قطعها الصوت.[4]
المفاهيم الأساسية
يمكن توضيح انتقال الصوت باستخدام نموذج يتكون من مجموعة من الأجسام الكروية المترابطة بواسطة النوابض.
من الناحية المادية الحقيقية، تمثل الكرات جزيئات المادة وتمثل النوابض الروابط بينها. يمر الصوت عبر النظام عن طريق ضغط وتوسيع النوابض، ونقل الطاقة الصوتية إلى المجالات المجاورة. يساعد هذا في نقل الطاقة بدوره إلى نوابض الكرة المجاورة (الروابط)، وما إلى ذلك.
تعتمد سرعة الصوت عبر النموذج على صلابة/قساوة النابض وكتلة الكرات. طالما أن التباعد بين الكرات يبقى ثابتاً، فإن النوابض/الروابط الأكثر صلابة تنقل الطاقة بشكل أسرع، بينما تنقل الكرات الأكبر الطاقة بشكل أبطأ.
في المادة الحقيقية ، تُعرف صلابة النوابض باسم معامل المرونة، وتتوافق الكتلة مع كثافة المادة. بالنظر إلى (ثبات باقي العوامل) الخاصة بجميع الأشياء الأخرى، سينتقل الصوت بشكل أبطأ في المواد الإسفنجية، وأسرع في المواد الأكثر صلابة. يمكن أيضاً فهم التأثيرات مثل التشتت والانعكاس باستخدام هذا النموذج.[citation needed]
على سبيل المثال، سينتقل الصوت في النيكل بمعدل 1.59 مرة أسرع منه في البرونز، بسبب زيادة صلابة النيكل عند نفس الكثافة تقريباً. وبالمثل، ينتقل الصوت في غاز الهيدروجين الخفيف ( پروتيوم) أسرع بنحو 1.41 مرة من غاز الهيدروجين الثقيل (ديوتريوم، نظراً لأن الديوتريوم له خصائص متشابهة ولكن ضعف الكثافة. في الوقت نفسه، ينتقل الصوت "من النوع المضغوط" في المواد الصلبة أسرع منه في السوائل، وأسرع في السوائل منه في الغازات، لأن ضغط المواد الصلبة أكثر صعوبة من السوائل، بينما السوائل بدورها تكون أكثر صعوبة في الضغط من الغازات.
تذكر بعض الكتب المدرسية خطأً أن سرعة الصوت تزداد مع زيادة الكثافة. يتم توضيح هذه الفكرة من خلال تقديم بيانات لثلاث مواد، مثل الهواء والماء والصلب، ولكل منها قابلية انضغاط مختلفة اختلافاً كبيراً، والتي تعوض أكثر من اختلافات الكثافة. مثال توضيحي للتأثيرين هو أن الصوت ينتقل في الماء أسرع بـ 4.3 مرات فقط من الهواء، على الرغم من الاختلافات الهائلة في انضغاط الوسيطتين. والسبب هو أن الكثافة الأكبر للمياه، والتي تعمل على "إبطاء" الصوت في الماء بالنسبة للهواء، تعوض تقريباً عن اختلافات الانضغاط في الوسطين.
يمكن ملاحظة مثال عملي في إدنبره عندما تم إطلاق "مدفع الساعة الواحدة" في الطرف الشرقي لقلعة إدنبره. عند الوقوف عند قاعدة الطرف الغربي من كاسل روك، يمكن سماع صوت البندقية من خلال الصخرة، قبل وصوله قليلاً بالطريق الهوائي، متأخراً جزئياً بسبب الطريق الأطول قليلاً. إنه فعال بشكل خاص إذا تم إطلاق تحية متعددة البنادق مثل "عيد ميلاد الملكة".
موجات الانضغاط والقص

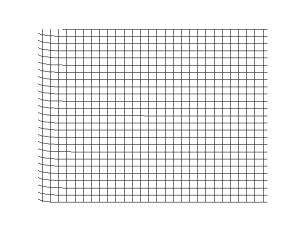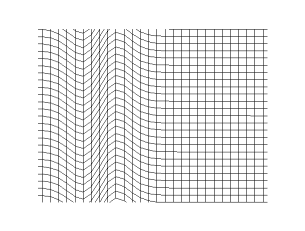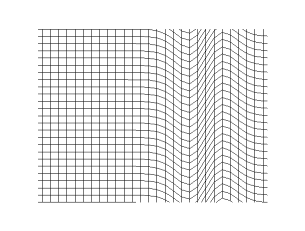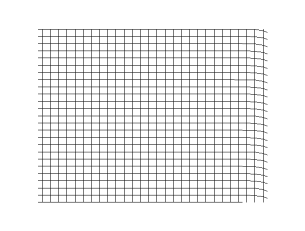
في الغازات أو السوائل، يتكون الصوت من موجات ضغط. في المواد الصلبة، تنتشر الموجات كنوعين مختلفين. ترتبط الموجة الطولية بالضغط وفك الضغط في اتجاه الانتقال، وهي نفس العملية في الغازات والسوائل، مع موجة ضغط مماثلة في المواد الصلبة. يتم دعم موجات الضغط فقط في الغازات والسوائل. نوع إضافي من الموجات، الموجة العرضية، وتسمى أيضاً موجة القص، تحدث فقط في المواد الصلبة لأن المواد الصلبة فقط هي التي تدعم التشوهات المرنة. بسبب التشوه المرن للوسط العمودي على اتجاه حركة الموجة؛ يسمى اتجاه تشوه القص بـ الاستقطاب لهذا النوع من الموجات. بشكل عام، تحدث الموجات العرضية كزوج من الاستقطاب المتعامد.
قد يكون لهذه الموجات المختلفة (موجات الضغط والاستقطابات المختلفة لموجات القص) سرعات مختلفة في نفس التردد. لذلك، يصلون إلى مراقب ما في أوقات مختلفة، من الأمثلة القصوى على ذلك الزلزال، حيث تصل موجات الانضغاط الحادة أولاً ثم تتأرجح الموجات العرضية بعد ثوانٍ.
يتم تحديد سرعة موجة الانضغاط في المائع بواسطة قابلية الانضغاط و الكثافة. في المواد الصلبة، تكون موجات الانضغاط مماثلة لتلك الموجودة في السوائل، اعتماداً على قابلية الانضغاط والكثافة، ولكن مع عامل إضافي لـ معامل القص الذي يؤثر على موجات الانضغاط بسبب الطاقات المرنة خارج المحور والتي تكون قادرة على التأثير على التوتر الفعال و الاسترخاء في ضغط. يتم تحديد سرعة موجات القص، التي يمكن أن تحدث فقط في المواد الصلبة، ببساطة من خلال معامل قص المادة الصلبة وكثافتها.
الانعكاس

| الوسط | السرعة بالأمتار في الثانية |
|---|---|
| الألومنيوم | 5,000 |
| الخشب | 4,110 |
| الزجاج | 4,540 |
| الطوب | 3,650 |
| الفولاذ | 5,200 |
| ماء البحر عند 25°م | 1,531 |
| الماء المقطر عند 25°م | 1,496 |
| الهواء عند 15°م | 340 |
إذا صحْتَ في اتجاه جدار كبير من الطوب، من مسافة عشرة أمتار على الأقل، فإنك ستسمع صدى صوتك. ينتج الصدى عندما تنعكس موجات الصوت من الجدار إلى أذنيك. وعمومًا، ينعكس جزء من الصَّوت، عندما تصطدم موجاته في وسط ما بجسم كبير من وسط آخر، كما حدث في حالة الموجات في الهواء بعد اصطدامها بجدار الطوب. والصوت الذي لا ينعكس يخترق الوسط الجديد. وتحدِّد سرعة الصوت في كل من الوسطين وكثافة الوسطين مقدار الانعكاس. وإذا كان الصوت ينتقل بنفس السرعة تقريبًا في كل من الوسطين، وكان لكل منهما نفس الكثافة تقريبًا، فإن ما ينعكس من الصوت يكون ضئيلاً، وسيخترق أغلب الصوت الوسط الجديد. وعلى عكس ذلك، ينعكس أغلب الصوت إذا كان هنالك اختلاف كبير في سرعة الصوت في الوسطين وكذلك في كثافتيهما. وتنتقل موجات الصوت في الهواء بسرعة تقل كثيرًا عن سرعتها في الطوب، كما أن كثافة الطوب تزيد كثيرًا عن كثافة الهواء، ولذلك ينعكس أغلب صوتك عندما تصيح باتجاه جدار الطوب.
الانكسار
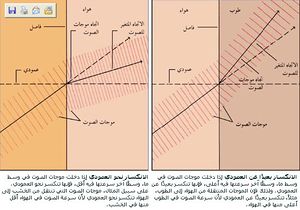
عندما تغادر موجات الصوت وسطًا وتدخل وسطًا آخر تختلف سرعتها، ويتغير اتجاهها. وينتج هذا التغيير في الاتجاه عن التغيُّر في سرعة الموجات، ويسمى انكسارًا. وإذا كانت سرعة موجات الصوت في الوسط الثاني أقل، تنكسر الموجات نحو العمودي. والعمودي خط وهمي يعامد الفاصل بين الوسطين. وإذا كانت سرعة الصوت في الوسط الثاني أكبر ، فإن الموجات تنكسر بعيدًا عن العمودي.
ويمكن أن تنكسر موجات الصوت أيضًا، إذا كانت سرعة الصوت تتغير من نقطة إلى نقطة في نفس الوسط. ففي هذه الحالة، تنحني الموجات نحو المنطقة ذات السرعة الأقل. وقد تكون لاحظت أن الصوت يُسمع من مسافة أبعد في الليل، مقارنة بنهار يوم ساطع الشمس. فأثناء النهار، يكون الهواء القريب من الأرض أدفأ من الهواء الذي يعلوه، ولذلك فإن موجات الصوت تنحني بعيدًا عن سطح الأرض نحو الهواء الأكثر برودة حيث تكون سرعتها أقل. وينتج عن انحناء الموجات بهذه الكيفية ضعف الصوت قرب سطح الأرض. أما في الليل، فإن الهواء القريب من سطح الأرض ويكون هو الأكثر برودة، فتنحني موجات الصوت نحو الأرض، مما يمكِّن من سماع الصوت القريب من الأرض من مسافات أبعد.
الحُيُود
تنتشر موجات الصوت التي تنتقل بمحاذاة مبنى مبتعدة حول ركن المبنى. وعندما تمر موجات الصوت عبر الباب، تنتشر حول حافته. ويُسمَّى انتشار الموجات حول حافة عائق تمر به، أو عند مرورها خلال فتحة ما الحُيُود. ويحدث الحيود كلما مرت موجات الصوت بعائق أو فتحة، ولكنه يصبح أوضح ما يكون إذا كان الطول الموجي للصوت طويلاً بالمقارنة مع حجم العائق أو الفتحة. ويُمكِّنك الحيود من سماع الصوت حول ركن، حتى في غياب مسار مستقيم من مصدر الصوت إلى أذنيك. انظر: الحيود.
الرنين
هو تقوية الصوت. ويحدث عندما تنتج قوة صغيرة متكررة اهتزازات أكبر وأكبر في جسم ما. ولكي يحدث الرنين، يلزم أن يكون للقوة المتكررة المبذولة تردد يساوي تردد رنين الجسم. وتردد الرنين هو تقريبًا التردد الذي يهتز به الجسم طبيعيًا، إذا تعرض لاضطراب ما. وقد قيل إن بعض المغنِّين في المسرحيات الغنائية يمكنهم أن يحطموا كوبًا زجاجيًا بغناء نغمة ذات تردد مساوٍ لتردد رنين الكوب، حيث تكبر الاهتزازات التي تحدث في الكوب، ويكبر الرنين حتى ينكسر الكوب.
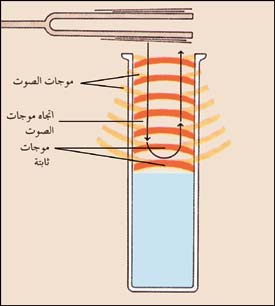
ومن الممكن إيضاح الرنين تجريبيًا بوساطة شوكة رنانة مهتزة، يمسك بها المرء فوق أنبوب مفتوح من ناحية ومغلق من الناحية الأخرى. فإذا كان طول الأنبوب ربع الطول الموجي للصوت الصادر عن الشوكة، فإن الموجات ستنتقل إلى أسفل الأنبوب وتنعكس من القاع. وفي هذه الحالة، تشكل الموجات المنعكسة مع الموجات الأصلية نمطًا موجيًا يبدو ساكنًا. وتسمى مثل هذه الأنماط الموجات الثابتة. وعندما تتكون الموجات الثابتة في الأنبوب، يكون عمود الهواء داخل الأنبوب في حالة رنين مع الشوكة الرنانة. وتجعل الموجات الثابتة في الأنبوب الهواء المحيط يهتز باتساع أكبر مما ينتج عنه صوت أكثر ارتفاعًا.
ويزيد الرنين من ارتفاع الصوت الذي تحدثه الكثير من الآلات الموسيقية. فالآلات الهوائية، على سبيل المثال، تنتج الرنين بنفس كيفية الشوكة الرنانة والأنبوب. تنشأ الموجات الثابتة في عمود الهواء داخل الآلة، فتجعله في حالة رنين مع الاهتزازات عند فتحة الفم، مكبرًا بذلك صوت الآلة.
الضربات
عندما تصدر نبرتان بترددين مختلفتين اختلافًا طفيفًا في الوقت نفسه، فإن ما يسمعه المرء يكون صوتًا واحدًا يرتفع وينخفض على فترات منتظمة. وتسمى هذه التغيرات الدورية في ارتفاع الصوت الضربات. وتنتج الضربات لأن موجات الصوت من النبرتين تتراكبان وتتداخلان. ويقال عن تداخل الموجات المشتركة إنه تداخل بنّاء إذا تطابقت الضغوط مع الضغوط والتخلخلات مع التخلخلات. ففي هذه الحالة، تقوِّي الموجات بعضها بعضًا منتجة صوتًا أكثر ارتفاعًا. ويكون التداخل هدامًا إذا تطابقت الضغوط مع التخلخلات. وفي هذه الحالة يتلاشى الصوت أو يكون ضعيفًا. وبسبب الاختلاف الطفيف في التردد، تتعاقب فترات التداخل البناء والتداخل الهدام، فيرتفع الصوت ثم ينخفض، منتجًا الضربات.
يساوي عدد الضربات في الثانية، ويسمى تردد الضربات، الفرق بين تردديْ النبرتين. فعند صدور نبرة بتردد 256 هرتز، ونبرة بتردد 257 هرتز في الوقت ذاته، على سبيل المثال، يسمع المرء ضربة واحدة في كل ثانية.
المعادلات
يتم تمثيل سرعة الصوت في مجموعة الرموز الرياضية بالحرف c، من الكلمة اللاتينية celeritas التي تعني السرعة.
بالنسبة للسوائل بشكل عام، تُعطى سرعة الصوت c بواسطة معادلة نيوتن-لابلاس:
حيث
- Ks معامل الصلابة، المتساوي معامل الحجم (أو معامل مرونة الحجم للغازات);
- الكثافة.
وهكذا، تزداد سرعة الصوت مع زيادة صلابة (مقاومة الجسم المرن للتشوه بواسطة القوة المطبقة) للمادة وتنخفض مع زيادة الكثافة. بالنسبة للغازات المثالية، فإن معامل الكتلة K هو ببساطة ضغط الغاز مضروباً في مؤشر ثابت الحرارة، وهو ما يقرب من 1.4 للهواء في ظل الظروف العادية للضغط ودرجة الحرارة.
بالنسبة إلى معادلات الحالة العامة، إذا تم استخدام الميكانيكا الكلاسيكية، فيمكن اشتقاق سرعة الصوت c[7] كالتالي:
لنعتبر أن الموجة الصوتية تنتشر بسرعة من خلال أنبوب محاذاة مع المحور ومساحة المقطع العرضي . في الفترة الزمنية تتحرك بطول . في الحالة الثابتة، يكون معدل تدفق الكتلة هو نفسه عند طرفي الأنبوب، وبالتالي فإن تدفق الكتلة .وفقاً لـ قانون نيوتن الثاني، توفر قوة تدرج الضغط التسارع:
ولذلك:
حيث
- P الضغط;
- هي الكثافة و يؤخذ المشتق متماثلاً، أي ثابت الانتروپيا s. وذلك لأن الموجة الصوتية تنتقل بسرعة كبيرة بحيث يمكن تقريب انتشارها على أنها عملية ثابتة الحرارة.
إذا كانت التأثيرات النسبية مهمة ،يتم حساب سرعة الصوت من معادلات أويلر النسبية.
في وسط غير مشتت، تكون سرعة الصوت مستقلة عن تردد الصوت، وبالتالي فإن سرعات نقل الطاقة وانتشار الصوت هي نفسها لجميع الترددات. يشكل الهواء، وهو خليط من الأكسجين والنيتروجين، وسطاً غير مشتت. ومع ذلك، يحتوي الهواء على كمية صغيرة من ثاني أكسيد الكربون CO2 وهو "وسط مشتت"، ويسبب تشتت الهواء عند ترددات الموجات فوق الصوتية (> 28 kHz)[8]
في وسط مشتت، تكون سرعة الصوت تابع لتردد الصوت، من خلال علاقة التشتت. ينتشر كل مكون تردد بسرعته الخاصة، والتي تسمى سرعة الطور، بينما تنتشر طاقة الاضطراب عند سرعة الزمرة. تحدث نفس الظاهرة مع موجات الضوء. راجع التشتت البصري للحصول على وصف.
الاعتماد على خصائص الوسط
سرعة الصوت متغيرة وتعتمد على خصائص المادة التي تنتقل الموجة من خلالها. في المواد الصلبة، تعتمد سرعة الموجات العرضية (أو القص) على تشوه القص تحت إجهاد القص (يسمى معامل القص)، وكثافة الوسط. تعتمد الموجات الطولية (أو الانضغاطية) في المواد الصلبة على نفس العاملين مع إضافة اعتماد على الانضغاطية.
في السوائل، تعتبر انضغاطية الوسيط وكثافته هما العاملان المهمان فقط، لأن السوائل لا تنقل إجهادات القص. في السوائل غير المتجانسة، مثل السائل المملوء بفقاعات الغاز، تؤثر كثافة السائل وانضغاطية الغاز على سرعة الصوت بطريقة مضافة، كما هو موضح في تأثير الشوكولاتة الساخنة.
في الغازات، ترتبط قابلية الانضغاط الحافظة للحرارة ارتباطاً مباشراً بالضغط من خلال نسبة السعة الحرارية (مؤشر ثابت الحرارة)، بينما يرتبط الضغط والكثافة عكسياً بدرجة الحرارة والوزن الجزيئي، مما يجعل فقط الخصائص المستقلة تماماً لـ درجة الحرارة و التركيب الجزيئي مهم (يمكن تحديد نسبة السعة الحرارية حسب درجة الحرارة والبنية الجزيئية، لكن الوزن الجزيئي البسيط لا يكفي لتحديده).
ينتشر الصوت بشكل أسرع في غازات الوزن الجزيئي المنخفض مثل الهليوم أكثر مما ينتشر في الغازات الثقيلة مثل زينون. بالنسبة للغازات الأحادية، تبلغ سرعة الصوت حوالي 75٪ من متوسط السرعة التي تتحرك بها الذرات في هذا الغاز.
بالنسبة إلى الغاز المثالي يكون التركيب الجزيئي ثابتاً، وبالتالي تعتمد سرعة الصوت فقط على درجة الحرارة. عند درجة حرارة ثابتة، لا يؤثر ضغط الغاز على سرعة الصوت، لأن الكثافة ستزداد، وبما أن الضغط و الكثافة (يتناسبان أيضاً مع الضغط) لهما تأثيرات متساوية ولكن معاكسة على السرعة من الصوت، وإلغاء المساهمتين بالضبط. بطريقة مماثلة، تعتمد موجات الانضغاط في المواد الصلبة على الانضغاطية والكثافة - تماماً كما في السوائل - ولكن في الغازات، تساهم الكثافة في الانضغاط بطريقة تجعل جزءاً من كل سمة من العوامل، تاركاً الاعتماد فقط على درجة الحرارة، الوزن الجزيئي ونسبة السعة الحرارية التي يمكن اشتقاقها بشكل مستقل من درجة الحرارة والتركيب الجزيئي (انظر المشتقات أدناه). وبالتالي، بالنسبة لغاز واحد معين (بافتراض أن الوزن الجزيئي لا يتغير) وعلى مدى درجة حرارة صغير (تكون السعة الحرارية فيه ثابتة نسبياً)، تصبح سرعة الصوت معتمدة على درجة حرارة الغاز فقط.
في النظام غير المثالي للغاز، حيث تُستخدم معادلة غاز ڤان در ڤالز، فإن التناسب ليس دقيقاً، وهناك اعتماد بسيط لسرعة الصوت على ضغط الغاز.
للرطوبة تأثير صغير ولكن يمكن قياسه على سرعة الصوت (مما يؤدي إلى زيادة بنحو 0.1٪ - 0.6٪)، لأنه يتم استبدال جزيئات الأكسجين و النيتروجين في الهواء بجزيئات أخف من الماء. وهذا تأثير خلط بسيط.
اختلاف الارتفاع والآثار المترتبة على صوتيات الغلاف الجوي

في غلاف الأرض الجوي، العامل الرئيسي الذي يؤثر على سرعة الصوت هو درجة الحرارة. بالنسبة لغاز مثالي معين بسعة حرارية ثابتة وتركيب ثابت، فإن سرعة الصوت تعتمد "فقط" على درجة الحرارة؛ راجع التفاصيل أدناه. في مثل هذه الحالة المثالية، فإن تأثيرات الكثافة المنخفضة وضغط الارتفاع المنخفض تلغي بعضها البعض، باستثناء التأثير المتبقي لدرجة الحرارة.
نظراً لتنافص درجة الحرارة (وبالتالي سرعة الصوت) مع زيادة الارتفاع حتى 11 km، فإن الصوت ينكسر لأعلى، بعيداً عن المستمعين على الأرض، مما يخلق ظل صوتي على مسافة ما من المصدر.[9] يشار إلى انخفاض سرعة الصوت مع الارتفاع بأنه تدرج سالب لسرعة الصوت.
ومع ذلك، هناك اختلافات في هذا الاتجاه أعلى من 11 km. على وجه الخصوص، في الستراتوسفير أعلاه حوالي 20 km، تزداد سرعة الصوت مع الارتفاع، بسبب زيادة درجة الحرارة من التسخين داخل طبقة الأوزون. ينتج عن هذا سرعة موجبة لتدرج الصوت في هذه المنطقة. لا تزال هناك منطقة عالية جداً أخرى من التدرج الموجب تحدث على ارتفاعات، في الغلاف الحراري المسمى بشكل مناسب فوق 90 km.
الصيغة العملية للهواء الجاف
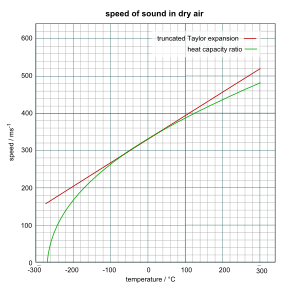
يمكن حساب السرعة التقريبية للصوت في الهواء الجاف (0٪ رطوبة)، بالأمتار في الثانية، عند درجات حرارة قريبة من 0 °C، من: حيث هي درجة الحرارة بالدرجة سلسيوس (°C).[10]
هذه المعادلة مشتقة من أول شرطين من منشور تايلور للمعادلة الأكثر دقة التالية:
ينتج عن قسمة الجزء الأول وضرب الجزء الثاني على الجانب الأيمن في √273.15 الشكل المكافئ تماماً
والتي يمكن كتابتها أيضاً
حيث يشير الحرف T إلى درجة الحرارة المطلقة.
تستند قيمة 331.3 m/s، والتي تمثل السرعة عند 0 °C (أو 273.15 K) إلى القيم النظرية (وبعضها مقاسة) لـ نسبة السعة الحرارية،γ، بالإضافة إلى حقيقة أنه في 1 ضغط جوي يتم وصف الهواء الحقيقي جيداً من خلال التقريب المثالي للغاز. قد تختلف القيم الشائعة لسرعة الصوت عند 0 °C من 331.2 إلى 331.6 بسبب الافتراضات التي تم إجراؤها عند حسابها. إذا افترضنا أن الغاز المثالي γ هو 7/5 = 1.4 بالضبط، يتم حساب سرعة 0 °C (انظر القسم أدناه) لتكون 331.3 m/s، المعامل المستخدم أعلاه.
هذه المعادلة صحيحة لنطاق درجة حرارة أوسع بكثير، لكنها لا تزال تعتمد على تقريب نسبة السعة الحرارية كونها مستقلة عن درجة الحرارة، ولهذا السبب ستفشل، خاصة في درجات الحرارة المرتفعة. إنه يعطي تنبؤات جيدة في الظروف الجافة والباردة والضغط المنخفض نسبياً، مثل الطبقة الجوية العليا للأرض. وتفشل المعادلة عند ضغوط منخفضة للغاية وأطوال موجية قصيرة، بسبب الاعتماد على افتراض أن الطول الموجي للصوت في الغاز أطول بكثير من متوسط المسار الحر بين تصادمات جزيئات الغاز. سيتم تحديد اشتقاق من هذه المعادلات في القسم التالي.
الرسم البياني الذي يقارن نتائج المعادلتين على اليمين، باستخدام قيمة مختلفة قليلاً لـ 331.5 m/s لسرعة الصوت عند 0 °C.[11]
التفاصيل
سرعة الصوت في الغازات المثالية والهواء
بالنسبة للغاز المثالي، يتم إعطاء K (معامل الحجم في المعادلات أعلاه، أي ما يعادل C، معامل الصلابة في المواد الصلبة) بواسطة
وهكذا، من معادلة نيوتن-لابلاس أعلاه، تُعطى سرعة الصوت في الغاز المثالي
حيث
- γ هو نسبة السعة الحرارية المعروف أيضاً باسم عامل التمدد المتساوي. هي نسبة الحرارة النوعية لغاز عند ضغط ثابت إلى حرارة غاز عند حجم ثابت () وتنشأ لأن موجة الصوت الكلاسيكية تحث على ضغط ثابت الحرارة، حيث الضغط ليس لديه الوقت الكافي للتخلص من نبض الضغط، وبالتالي يساهم في الضغط الناجم عن الانضغاط;
- p هي الضغط;
- ρ هي الكثافة.
باستخدام قانون الغازات المثالية لاستبدال p بـ nRT/V واستبدال ρ بـ nM/V تصبح معادلة الغاز المثالي
حيث
- cideal هي سرعة الصوت في الغازات المثالية;
- R (حوالي 8.314463 J·K−1·mol−1) هي ثابت غازي مولي (ثابت الغاز العام);[12]
- k هي ثابت بولتسمان;
- γ (گاما) هي نسبة السعة الحرارية. في درجة حرارة الغرفة، حيث يتم تقسيم الطاقة الحرارية بالكامل إلى دوران (تكون الدورات مثارة بشكل تام) ولكن التأثيرات الكمية تمنع إثارة أوضاع الاهتزاز، تكون القيمة 7/5 = 1.400 للجزيئات ثنائية الذرة، وفقاً للنظرية الحركية. تم قياس گاما بشكل تجريبي عبر نطاق من 1.3991 إلى 1.403 عند 0 °C، للهواء. گاما هي بالضبط 5/3 = 1.6667 للغازات أحادية الذرة مثل الغازات النبيلة وهي 8/6 = 1.3333 لغازات الجزيئات الثلاثية، مثل الماء، ليست خطية مشتركة (الغاز الثلاثي الخطي المشترك مثل ثاني أكسيد الكربون يعادل غاز ثنائي الذرة لأغراضنا هنا);
- T هي درجة الحرارة المطلقة;
- M هي الكتلة المولية للغاز. متوسط الكتلة المولية للهواء الجاف حوالي 0.028,964,5 kg/mol;[citation needed]
- n هو عدد المولات;
- m هي كتلة جزيء واحد.
تنطبق هذه المعادلة فقط عندما تكون الموجة الصوتية اضطراباً صغيراً في الحالة المحيطة، ويتم استيفاء بعض الشروط الأخرى المذكورة، كما هو مذكور أدناه. تم إيجاد القيم المحسوبة لـ cair والتي تختلف قليلاً عن القيم المحددة تجريبياً.[13]
اشتهر نيوتن بسرعة الصوت قبل معظم تطورات الديناميكا الحرارية ولذلك استخدم بشكل غير صحيح حسابات الحرارة اللاتبادلية بدلاً من ثابت الحرارة. كانت نتيجته تفتقد إلى عامل γ لكنها كانت صحيحة.
يعطي الاستبدال العددي للقيم المذكورة أعلاه تقريباً مثالياً لسرعة الصوت للغازات، والتي تكون دقيقة عند ضغوط وكثافة الغاز المنخفضة نسبياً (بالنسبة للهواء، يشمل ذلك ظروف مستوى سطح البحر القياسية للأرض). أيضاً، بالنسبة للغازات ثنائية الذرة، يتطلب استخدام γ = 1.4000 أن يكون الغاز موجوداً في نطاق درجة حرارة عالية بما يكفي لتحفيز السعة الحرارية الدورانية بالكامل (على سبيل المثال، يتم استخدام الدوران الجزيئي بشكل كامل فاصل أو خزان للطاقة الحرارية); ولكن في الوقت نفسه، يجب أن تكون درجة الحرارة منخفضة بدرجة كافية بحيث لا تساهم أنماط الاهتزاز الجزيئي في أي سعة حرارية (على سبيل المثال، تدخل حرارة ضئيلة في الاهتزاز، حيث أن جميع أوضاع الكم الاهتزازية فوق وضع الطاقة الدنيا، لديها طاقات عالية جداً بحيث لا يمكن ملؤها بواسطة عدد كبير من الجزيئات في درجة الحرارة هذه). بالنسبة للهواء، يتم استيفاء هذه الشروط في درجة حرارة الغرفة، وكذلك درجات حرارة أقل بكثير من درجة حرارة الغرفة (انظر الجداول أدناه). انظر القسم الخاص بالغازات في السعة الحرارية النوعية لمزيد من المناقشة الكاملة لهذه الظاهرة.
بالنسبة للهواء، نقدم الاختصار
بالإضافة إلى ذلك، ننتقل إلى درجة الحرارة المئوية = T − 273.15، وهو أمر مفيد لحساب سرعة الهواء في المنطقة القريبة 0 °C (حوالي 273 كلڤن). ثم، للهواء الجاف،
حيث (ثيتا) هي درجة الحرارة بالدرجات سلسيوس (°C).
باستبدال القيم العددية
ثابت الغازات العام بوحدة J/مول/كلڤن، و
متوسط الكتلة المولية للهواء بالكيلو غرام; واستخدام القيمة المثالية للغاز ثنائي الذرة γ = 1.4000، لدينا
أخيراً، ينتج عن منشور تايلور للجذر التربيعي المتبقي في
يتضمن الاشتقاق أعلاه المعادلتين الأوليين الواردتين في قسم "المعادلة العملية للهواء الجاف" أعلاه.
آثار قص الريح
The speed of sound varies with temperature. Since temperature and sound velocity normally decrease with increasing altitude, sound is refracted upward, away from listeners on the ground, creating an acoustic shadow at some distance from the source.[9] Wind shear of 4 m/(s · km) can produce refraction equal to a typical temperature lapse rate of 7.5 °C/km.[14] Higher values of wind gradient will refract sound downward toward the surface in the downwind direction,[15] eliminating the acoustic shadow on the downwind side. This will increase the audibility of sounds downwind. This downwind refraction effect occurs because there is a wind gradient; the sound is not being carried along by the wind.[16]
For sound propagation, the exponential variation of wind speed with height can be defined as follows:[17]
where
- U(h) is the speed of the wind at height h;
- ζ is the exponential coefficient based on ground surface roughness, typically between 0.08 and 0.52;
- dU/dH(h) is the expected wind gradient at height h.
In the 1862 American Civil War Battle of Iuka, an acoustic shadow, believed to have been enhanced by a northeast wind, kept two divisions of Union soldiers out of the battle,[18] because they could not hear the sounds of battle only 10 km (six miles) downwind.[19]
الجداول
In the standard atmosphere:
- T0 is 273.15 K (= 0 °C = 32 °F), giving a theoretical value of 331.3 m/s (= 1086.9 ft/s = 1193 km/h = 741.1 mph = 644.0 kn). Values ranging from 331.3 to 331.6 m/s may be found in reference literature, however;
- T20 is 293.15 K (= 20 °C = 68 °F), giving a value of 343.2 m/s (= 1126.0 ft/s = 1236 km/h = 767.8 mph = 667.2 kn);
- T25 is 298.15 K (= 25 °C = 77 °F), giving a value of 346.1 m/s (= 1135.6 ft/s = 1246 km/h = 774.3 mph = 672.8 kn).
In fact, assuming an ideal gas, the speed of sound c depends on temperature only, not on the pressure or density (since these change in lockstep for a given temperature and cancel out). Air is almost an ideal gas. The temperature of the air varies with altitude, giving the following variations in the speed of sound using the standard atmosphere—actual conditions may vary.
| أثر درجة الحرارة | |||
|---|---|---|---|
| in °C | c in m·s-1 | ρ in kg·m-3 | Z in N·s·m-3 |
| −10 | 325.2 | 1.342 | 436.1 |
| −5 | 328.3 | 1.317 | 432.0 |
| 0 | 331.3 | 1.292 | 428.4 |
| +5 | 334.3 | 1.269 | 424.3 |
| +10 | 337.3 | 1.247 | 420.6 |
| +15 | 340.3 | 1.225 | 416.8 |
| +20 | 343.2 | 1.204 | 413.2 |
| +25 | 346.1 | 1.184 | 409.8 |
| +30 | 349.0 | 1.165 | 406.3 |
- is the temperature in °C
- c is the speed of sound in m·s-1
- ρ is the density in kg·m-3
- Z is the characteristic acoustic impedance in N·s·m-3 (Z=ρ·c)
Given normal atmospheric conditions, the temperature, and thus speed of sound, varies with altitude:
| الارتفاع | درجة الحرارة | m·s-1 | km·h-1 | mph | knots |
| Sea level | 15 °C (59 °F) | 340 | 1225 | 761 | 661 |
| 11 000 m−20 000 m (Cruising altitude of commercial jets, and first supersonic flight) |
−57 °C (−70 °F) | 295 | 1062 | 660 | 573 |
| 29 000 m (Flight of X-43A) | −48 °C (−53 °F) | 301 | 1083 | 673 | 585 |
تأثير التردد وتكوين الغاز
اعتبارات طبيعية عامة
The medium in which a sound wave is travelling does not always respond adiabatically, and as a result, the speed of sound can vary with frequency.[20]
The limitations of the concept of speed of sound due to extreme attenuation are also of concern. The attenuation which exists at sea level for high frequencies applies to successively lower frequencies as atmospheric pressure decreases, or as the mean free path increases. For this reason, the concept of speed of sound (except for frequencies approaching zero) progressively loses its range of applicability at high altitudes.[13] The standard equations for the speed of sound apply with reasonable accuracy only to situations in which the wavelength of the sound wave is considerably longer than the mean free path of molecules in a gas.
The molecular composition of the gas contributes both as the mass (M) of the molecules, and their heat capacities, and so both have an influence on speed of sound. In general, at the same molecular mass, monatomic gases have slightly higher speed of sound (over 9% higher) because they have a higher γ (5/3 = 1.66...) than diatomics do (7/5 = 1.4). Thus, at the same molecular mass, the speed of sound of a monatomic gas goes up by a factor of
This gives the 9% difference, and would be a typical ratio for speeds of sound at room temperature in helium vs. deuterium, each with a molecular weight of 4. Sound travels faster in helium than deuterium because adiabatic compression heats helium more since the helium molecules can store heat energy from compression only in translation, but not rotation. Thus helium molecules (monatomic molecules) travel faster in a sound wave and transmit sound faster. (Sound travels at about 70% of the mean molecular speed in gases; the figure is 75% in monatomic gases and 68% in diatomic gases).
Note that in this example we have assumed that temperature is low enough that heat capacities are not influenced by molecular vibration (see heat capacity). However, vibrational modes simply cause gammas which decrease toward 1, since vibration modes in a polyatomic gas give the gas additional ways to store heat which do not affect temperature, and thus do not affect molecular velocity and sound velocity. Thus, the effect of higher temperatures and vibrational heat capacity acts to increase the difference between the speed of sound in monatomic vs. polyatomic molecules, with the speed remaining greater in monatomics.
تطبيق عملي على الهواء
By far, the most important factor influencing the speed of sound in air is temperature. The speed is proportional to the square root of the absolute temperature, giving an increase of about 0.6 m/s per degree Celsius. For this reason, the pitch of a musical wind instrument increases as its temperature increases.
The speed of sound is raised by humidity. The difference between 0% and 100% humidity is about 1.5 m/s at standard pressure and temperature, but the size of the humidity effect increases dramatically with temperature.
The dependence on frequency and pressure are normally insignificant in practical applications. In dry air, the speed of sound increases by about 0.1 m/s as the frequency rises from 10 Hz to 100 Hz. For audible frequencies above 100 Hz it is relatively constant. Standard values of the speed of sound are quoted in the limit of low frequencies, where the wavelength is large compared to the mean free path.[21]
As shown above, the approximate value 1000/3 = 333.33... m/s is exact a little below 5 °C and is a good approximation for all "usual" outside temperatures (in temperate climates, at least), hence the usual rule of thumb to determine how far lightning has struck: count the seconds from the start of the lightning flash to the start of the corresponding roll of thunder and divide by 3: the result is the distance in kilometers to the nearest point of the lightning bolt.
رقم ماخ
رقم ماخ، الكمية المفيدة في الديناميكا الهوائية، هو نسبة السرعة في الجو إلى السرعة المحلية للصوت. وعلى ارتفاع، للأسباب المشروحة، فإن رقم ماخ هو دالة في درجة الحرارة. إلا أن أجهزة قياس الطيران تعمل باستخدام فارق الضغط لحساب رقم ماخ، وليس درجة الحرارة. الافتراض هو أن ضغطاً معيناً يمثل ارتفاعاً معيناً، ولذلك درجة حرارة قياسية. تحتاج أجهزة قياس الطيران إلى العمل بهذه الطريقة لأن ضغط الركود الذي يستشعره أنبوب پيتو يعتمد على الارتفاع بالإضافة إلى السرعة.
الطرق التجريبية
توجد مجموعة من الطرق المختلفة لقياس الصوت في الهواء.
The earliest reasonably accurate estimate of the speed of sound in air was made by William Derham and acknowledged by Isaac Newton. Derham had a telescope at the top of the tower of the Church of St Laurence in Upminster, England. On a calm day, a synchronized pocket watch would be given to an assistant who would fire a shotgun at a pre-determined time from a conspicuous point some miles away, across the countryside. This could be confirmed by telescope. He then measured the interval between seeing gunsmoke and arrival of the sound using a half-second pendulum. The distance from where the gun was fired was found by triangulation, and simple division (distance/time) provided velocity. Lastly, by making many observations, using a range of different distances, the inaccuracy of the half-second pendulum could be averaged out, giving his final estimate of the speed of sound. Modern stopwatches enable this method to be used today over distances as short as 200–400 metres, and not needing something as loud as a shotgun.
طرق توقيت الطلقة الواحدة
The simplest concept is the measurement made using two microphones and a fast recording device such as a digital storage scope. This method uses the following idea.
If a sound source and two microphones are arranged in a straight line, with the sound source at one end, then the following can be measured:
- The distance between the microphones (x), called microphone basis.
- The time of arrival between the signals (delay) reaching the different microphones (t).
Then v = x/t.
طرق أخرى
In these methods, the time measurement has been replaced by a measurement of the inverse of time (frequency).
Kundt's tube is an example of an experiment which can be used to measure the speed of sound in a small volume. It has the advantage of being able to measure the speed of sound in any gas. This method uses a powder to make the nodes and antinodes visible to the human eye. This is an example of a compact experimental setup.
A tuning fork can be held near the mouth of a long pipe which is dipping into a barrel of water. In this system it is the case that the pipe can be brought to resonance if the length of the air column in the pipe is equal to (1 + 2n)λ/4 where n is an integer. As the antinodal point for the pipe at the open end is slightly outside the mouth of the pipe it is best to find two or more points of resonance and then measure half a wavelength between these.
Here it is the case that v = fλ.
قياسات عالية الدقة في الهواء
The effect of impurities can be significant when making high-precision measurements. Chemical desiccants can be used to dry the air, but will, in turn, contaminate the sample. The air can be dried cryogenically, but this has the effect of removing the carbon dioxide as well; therefore many high-precision measurements are performed with air free of carbon dioxide rather than with natural air. A 2002 review[22] found that a 1963 measurement by Smith and Harlow using a cylindrical resonator gave "the most probable value of the standard speed of sound to date." The experiment was done with air from which the carbon dioxide had been removed, but the result was then corrected for this effect so as to be applicable to real air. The experiments were done at 30 °C but corrected for temperature in order to report them at 0 °C. The result was 331.45 ± 0.01 m/s for dry air at STP, for frequencies from 93 Hz to 1,500 Hz.
الأوساط غير الغازية
سرعة الصوت في الكتل الصلبة
الجواسئ ثلاثية الأبعاد
In a solid, there is a non-zero stiffness both for volumetric deformations and shear deformations. Hence, it is possible to generate sound waves with different velocities dependent on the deformation mode. Sound waves generating volumetric deformations (compression) and shear deformations (shearing) are called pressure waves (longitudinal waves) and shear waves (transverse waves), respectively. In earthquakes, the corresponding seismic waves are called P-waves (primary waves) and S-waves (secondary waves), respectively. The sound velocities of these two types of waves propagating in a homogeneous 3-dimensional solid are respectively given by[23]
حيث
- K هي bulk modulus of the elastic materials;
- G هي shear modulus of the elastic materials;
- E هي معامل ينگ؛
- ρ هي الكثافة؛
- ν هي نسبة پواسون.
The last quantity is not an independent one, as E = 3K(1 − 2ν). Note that the speed of pressure waves depends both on the pressure and shear resistance properties of the material, while the speed of shear waves depends on the shear properties only.
Typically, pressure waves travel faster in materials than do shear waves, and in earthquakes this is the reason that the onset of an earthquake is often preceded by a quick upward-downward shock, before arrival of waves that produce a side-to-side motion. For example, for a typical steel alloy, K = 170 GPa, G = 80 GPa and ρ = 7,700 kg/m3, yielding a compressional speed csolid,p of 6,000 m/s.[23] This is in reasonable agreement with csolid,p measured experimentally at 5,930 m/s for a (possibly different) type of steel.[24] The shear speed csolid,s is estimated at 3,200 m/s using the same numbers.
الجواسئ أحادية البعد
The speed of sound for pressure waves in stiff materials such as metals is sometimes given for "long rods" of the material in question, in which the speed is easier to measure. In rods where their diameter is shorter than a wavelength, the speed of pure pressure waves may be simplified and is given by:[25]
where E is Young's modulus. This is similar to the expression for shear waves, save that Young's modulus replaces the shear modulus. This speed of sound for pressure waves in long rods will always be slightly less than the same speed in homogeneous 3-dimensional solids, and the ratio of the speeds in the two different types of objects depends on Poisson's ratio for the material.
سرعة الصوت في السوائل
In a fluid, the only non-zero stiffness is to volumetric deformation (a fluid does not sustain shear forces).
Hence the speed of sound in a fluid is given by
where K is the bulk modulus of the fluid.
الماء
In fresh water, sound travels at about 1481 m/s at 20 °C (see the External Links section below for online calculators).[26] Applications of underwater sound can be found in sonar, acoustic communication and acoustical oceanography.
ماء البحر
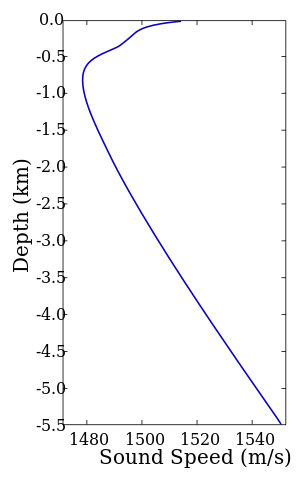
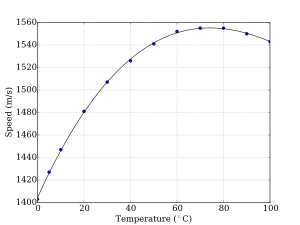
In salt water that is free of air bubbles or suspended sediment, sound travels at about 1500 m/s (1500.235 m/s at 1000 kilopascals, 10 °C and 3% salinity by one method).[27] The speed of sound in seawater depends on pressure (hence depth), temperature (a change of 1 °C ~ 4 m/s), and salinity (a change of 1‰ ~ 1 m/s), and empirical equations have been derived to accurately calculate the speed of sound from these variables.[28][29] Other factors affecting the speed of sound are minor. Since in most ocean regions temperature decreases with depth, the profile of the speed of sound with depth decreases to a minimum at a depth of several hundred metres. Below the minimum, sound speed increases again, as the effect of increasing pressure overcomes the effect of decreasing temperature (right).[30] For more information see Dushaw et al.[31]
An empirical equation for the speed of sound in sea water is provided by Mackenzie:[32]
حيث
- T is the temperature in degrees Celsius;
- S is the salinity in parts per thousand;
- z is the depth in metres.
The constants a1, a2, ..., a9 are
with check value 1550.744 m/s for T = 25 °C, S = 35 parts per thousand, z = 1,000 m. This equation has a standard error of 0.070 m/s for salinity between 25 and 40 ppt. See Technical Guides. Speed of Sound in Sea-Water for an online calculator.
(Note: The Sound Speed vs. Depth graph does not correlate directly to the MacKenzie formula. This is due to the fact that the temperature and salinity varies at different depths. When T and S are held constant, the formula itself is always increasing with depth.)
Other equations for the speed of sound in sea water are accurate over a wide range of conditions, but are far more complicated, e.g., that by V. A. Del Grosso[33] and the Chen-Millero-Li Equation.[31][34]
سرعة الصوت في الپلازما
سرعة الصوت في پلازما للحالة الشائعة حيث تكون الإلكترونات أسخن من الأيونات (ولكن ليست أسخن كثيراً) تعطيها الصيغة (انظر هنا)
حيث
- mi هي كتلة الأيون؛
- μ هي نسبة كتلة الأيون إلى كتلة الپروتون μ = mi/mp؛
- Te هي درجة حرارة الإلكترون؛
- Z هي حالة الشحنة؛
- k هي ثابت بولتسمان؛
- γ هي نسبة السعة الحرارية.
على عكس الغاز، فإن الضغط والكثافة يحددهما نوعان منفصلان: الضغط من الإلكترونات والكثافة من الأيونات. ويقترن الاثنان من خلال مجال كهربائي متقلب.
انظر أيضاُ
- Acoustoelastic effect
- موجة مرنة
- صوت الثانية
- دوي إختراق الصوت
- حاجز الصوت
- سرعات الصوت في العناصر
- الصوتيات تحت الماء
- اهتزاز
- قناة سوفار
مرئيات
| ما هي سرعة الصوت؟ لماذا ينعدم الصوت في الفضاء؟ |
المصادر
- ^ "The Speed of Sound". mathpages.com. Retrieved 3 May 2015.
- ^ Bannon, Mike; Kaputa, Frank (12 December 2014). "The Newton–Laplace Equation and Speed of Sound". Thermal Jackets. Retrieved 3 May 2015.
- ^ أ ب Murdin, Paul (25 December 2008). Full Meridian of Glory: Perilous Adventures in the Competition to Measure the Earth. Springer Science & Business Media. pp. 35–36. ISBN 9780387755342.
- ^ Fox, Tony (2003). Essex Journal. Essex Arch & Hist Soc. pp. 12–16.
- ^ APOD: 19 August 2007- A Sonic Boom
- ^ http://www.eng.vt.edu/fluids/msc/gallery/conden/mpegf14.htm
- ^ "17.2 Speed of Sound | University Physics Volume 1". courses.lumenlearning.com. Retrieved 2020-01-24.
- ^ Dean, E. A. (August 1979). Atmospheric Effects on the Speed of Sound, Technical report of Defense Technical Information Center
- ^ أ ب Everest, F. (2001). The Master Handbook of Acoustics. New York: McGraw-Hill. pp. 262–263. ISBN 978-0-07-136097-5.
- ^ Bies, D.A.; Hansen, C.H. (2009). Engineering Noise Control - Theory and Practice, 4th Edition. New York: CRC Press. pp. 18–19. ISBN 978-0-415-48707-8.
- ^ Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. (2000). Fundamentals of Acoustics, 4th Edition. New York: John Wiley & Sons. pp. 120-121. ISBN 0-471-84789-5.
- ^ "CODATA Value: molar gas constant". Physics.nist.gov. Retrieved 24 October 2010.
- ^ أ ب U.S. Standard Atmosphere, 1976, U.S. Government Printing Office, Washington, D.C., 1976.
- ^ Uman, Martin (1984). Lightning. New York: Dover Publications. ISBN 978-0-486-64575-9.
- ^ Volland, Hans (1995). Handbook of Atmospheric Electrodynamics. Boca Raton: CRC Press. p. 22. ISBN 978-0-8493-8647-3.
- ^ Singal, S. (2005). Noise Pollution and Control Strategy. Oxford: Alpha Science International. p. 7. ISBN 978-1-84265-237-4.
It may be seen that refraction effects occur only because there is a wind gradient and it is not due to the result of sound being convected along by the wind.
- ^ Bies, David (2009). Engineering Noise Control, Theory and Practice. London: CRC Press. p. 249. ISBN 978-0-415-26713-7.
As wind speed generally increases with altitude, wind blowing towards the listener from the source will refract sound waves downwards, resulting in increased noise levels.
- ^ Cornwall, Sir (1996). Grant as Military Commander. New York: Barnes & Noble. p. 92. ISBN 978-1-56619-913-1.
- ^ Cozens, Peter (2006). The Darkest Days of the War: the Battles of Iuka and Corinth. Chapel Hill: The University of North Carolina Press. ISBN 978-0-8078-5783-0.
- ^ A B Wood, A Textbook of Sound (Bell, London, 1946)
- ^ "Speed of Sound in Air". Phy.mtu.edu. Retrieved 13 June 2014.
- ^ Zuckerwar, Handbook of the speed of sound in real gases, p. 52
- ^ أ ب L. E. Kinsler et al. (2000), Fundamentals of acoustics, 4th Ed., John Wiley and sons Inc., New York, USA.
- ^ J. Krautkrämer and H. Krautkrämer (1990), Ultrasonic testing of materials, 4th fully revised edition, Springer-Verlag, Berlin, Germany, p. 497
- ^ Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. (2000). Fundamentals of Acoustics, 4th Edition. New York: John Wiley & Sons. pp. 70. ISBN 0-471-84789-5.
- ^ "Speed of Sound in Water at Temperatures between 32–212 oF (0–100 oC) — imperial and SI units". The Engineering Toolbox.
- ^ Wong, George S. K.; Zhu, Shi-ming (1995). "Speed of sound in seawater as a function of salinity, temperature, and pressure". The Journal of the Acoustical Society of America. 97 (3): 1732. Bibcode:1995ASAJ...97.1732W. doi:10.1121/1.413048.
- ^ APL-UW TR 9407 High-Frequency Ocean Environmental Acoustic Models Handbook, pp. I1-I2.
- ^ Robinson, Stephen (22 September 2005). "Technical Guides – Speed of Sound in Sea-Water". National Physical Laboratory. Retrieved 7 December 2016.
- ^ "How Fast Does Sound Travel?". Discovery of Sound in the Sea. University of Rhode Island. Retrieved 30 November 2010.
- ^ أ ب Dushaw, Brian D.; Worcester, P. F.; Cornuelle, B. D.; Howe, B. M. (1993). "On Equations for the Speed of Sound in Seawater". Journal of the Acoustical Society of America. 93 (1): 255–275. Bibcode:1993ASAJ...93..255D. doi:10.1121/1.405660.
- ^ Kenneth V., Mackenzie (1981). "Discussion of sea-water sound-speed determinations". Journal of the Acoustical Society of America. 70 (3): 801–806. Bibcode:1981ASAJ...70..801M. doi:10.1121/1.386919.
- ^ Del Grosso, V. A. (1974). "New equation for speed of sound in natural waters (with comparisons to other equations)". Journal of the Acoustical Society of America. 56 (4): 1084–1091. Bibcode:1974ASAJ...56.1084D. doi:10.1121/1.1903388.
- ^ Meinen, Christopher S.; Watts, D. Randolph (1997). "Further Evidence that the Sound-Speed Algorithm of Del Grosso Is More Accurate Than that of Chen and Millero". Journal of the Acoustical Society of America. 102 (4): 2058–2062. Bibcode:1997ASAJ..102.2058M. doi:10.1121/1.419655.
وصلات خارجية
- Calculation: Speed of sound in air and the temperature
- Speed of sound - temperature matters, not air pressure
- Properties Of The U.S. Standard Atmosphere 1976
- The Speed of Sound at MathPages
- How to measure the speed of sound in a laboratory
- Speed of sound in water and water steam as function of pressure & temperature
- Teaching resource for 14-16yrs on sound including speed of sound
- Technical Guides - Speed of Sound in Pure Water
- Technical Guides - Speed of Sound in Sea-Water
- NewByte standard atmosphere calculator and speed converter
- Did sound once travel at light speed? - If the speed of sound was greater just after the big bang, it could solve a longstanding mystery over the universe's background temperature (New Scientist, 9 April 2008)