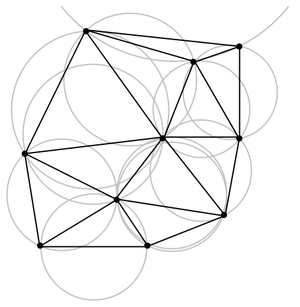
تثليث ديلاوني
في الرياضيات والهندسة الرياضية الحاسوبية، تثليث ديلاوني إنگليزية: Delaunay triangulation لمجموعة P من النقاط في المستوي هو تثليث DT(P) بحيث أن لا يوجد أي نقطة من P تكون داخل الدائرة المحيطة بأي مثلث في DT(P). يعمل تثليث ديلاوني على تعظيم أصغر زاوية في جميع مثلثات التثليث، وبذلك يتم تفادي إنشاء مثلثات رفيعة جداً. تم اختراع طريقة التثليث هذه من قبل بوريس ديلاوني في عام 1934. [1]
بحسب تعريف ديلاوني، فإن الدائرة المحيطة بمثلث تم إنشاءه من ثلاث نقاط من مجموعة النقاط تكون دائرة فارغة إذا لم تحتوي هذه الدائرة غير النقاط الثلاثة المعرفة لها. وعليه فإن شرط ديلاوني ينص أن الشبكة المثلثية تكون تثليث ديلاوني إذا كانت جميع الدوائر المحيطة بالمثلثات هي دوائر فارغة.
مراجع
- ^ B. Delaunay: Sur la sphère vide, Izvestia Akademii Nauk SSSR, Otdelenie Matematicheskikh i Estestvennykh Nauk, 7:793-800, 1934
وصلات خارجية
This article may include material from Wikimedia licensed under CC BY-SA 4.0. Please comply with the license terms.