وزن
| Weight | |
|---|---|
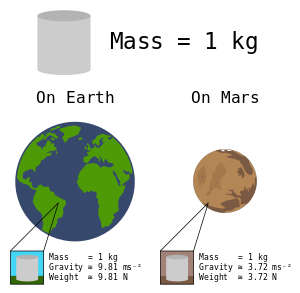 A diagram explaining the mass and weight | |
الرموز الشائعة | |
| الوحدة الدولية | newton (N) |
وحدات أخرى | pound-force (lbf) |
| In الوحدة الدولية الأساسية | kg⋅m⋅s−2 |
| بعد قياسي SI | |
| Extensive? | Yes |
| Intensive? | No |
| Conserved? | No |
اشتقاقات من كميات أخرى | |
| البعد | |
الوزن هو قوة جذب الأرض للجسم. وهي طريقة لتحديد كمية مادة ما، تختلف وحدات أو معيارية الأوزان من مادة ما إلى أخرى عند قياسها فبعضها مخصص للأوزان القليلة أو الخفيفة أو الثمينة ومنها ما هو للتحديد التقريبي للمادة.
In science and engineering, the weight of an object is the force acting on the object due to acceleration or gravity.[1][2][3]
Some standard textbooks[4] define weight as a vector quantity, the gravitational force acting on the object. Others[5][6] define weight as a scalar quantity, the magnitude of the gravitational force. Yet others[7] define it as the magnitude of the reaction force exerted on a body by mechanisms that counteract the effects of gravity: the weight is the quantity that is measured by, for example, a spring scale. Thus, in a state of free fall, the weight would be zero. In this sense of weight, terrestrial objects can be weightless: so if one ignores air resistance, one could say the legendary apple falling from the tree, on its way to meet the ground near Isaac Newton, was weightless.
The unit of measurement for weight is that of force, which in the International System of Units (SI) is the newton. For example, an object with a mass of one kilogram has a weight of about 9.8 newtons on the surface of the Earth, and about one-sixth as much on the Moon. Although weight and mass are scientifically distinct quantities, the terms are often confused with each other in everyday use (e.g. comparing and converting force weight in pounds to mass in kilograms and vice versa).[8]
Further complications in elucidating the various concepts of weight have to do with the theory of relativity according to which gravity is modeled as a consequence of the curvature of spacetime. In the teaching community, a considerable debate has existed for over half a century on how to define weight for their students. The current situation is that a multiple set of concepts co-exist and find use in their various contexts.[2]
التاريخ


تعريفات

Several definitions exist for weight, not all of which are equivalent.[3][10][11][12]
التعريف الثقالي
The most common definition of weight found in introductory physics textbooks defines weight as the force exerted on a body by gravity.[1][12] This is often expressed in the formula W = mg, where W is the weight, m the mass of the object, and g gravitational acceleration.
الكتلة
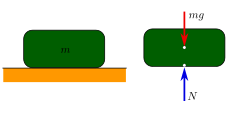
الأرض تجذب الاجسام بقوة تؤثر باتجاه رأسي إلى أسفل تسمى قوة الجاذبية الأرضية ، و اتفق العلماء على تسمية قوة جذب الأرض بوزن الجسم و يستخدم الميزان الزنبركي في قياس الأوزان.
This table shows the variation of acceleration due to gravity (and hence the variation of weight) at various locations on the Earth's surface.[13]
| Location | Latitude | m/s2 |
|---|---|---|
| Equator | 0° | 9.7803 |
| Sydney | 33°52′ S | 9.7968 |
| Aberdeen | 57°9′ N | 9.8168 |
| North Pole | 90° N | 9.8322 |
The historic use of "weight" for "mass" also persists in some scientific terminology – for example, the chemical terms "atomic weight", "molecular weight", and "formula weight", can still be found rather than the preferred "atomic mass" etc.
In a different gravitational field, for example, on the surface of the Moon, an object can have a significantly different weight than on Earth. The gravity on the surface of the Moon is only about one-sixth as strong as on the surface of the Earth. A one-kilogram mass is still a one-kilogram mass (as mass is an intrinsic property of the object) but the downward force due to gravity, and therefore its weight, is only one-sixth of what the object would have on Earth. So a man of mass 180 pounds weighs only about 30 pounds-force when visiting the Moon.
SI units
In most modern scientific work, physical quantities are measured in SI units. The SI unit of weight is the same as that of force: the newton (N) – a derived unit which can also be expressed in SI base units as kg⋅m/s2 (kilograms times meters per second squared).[14]
In commercial and everyday use, the term "weight" is usually used to mean mass, and the verb "to weigh" means "to determine the mass of" or "to have a mass of". Used in this sense, the proper SI unit is the kilogram (kg).[14]
Pound and other non-SI units
In United States customary units, the pound can be either a unit of force or a unit of mass.[15] Related units used in some distinct, separate subsystems of units include the poundal and the slug. The poundal is defined as the force necessary to accelerate an object of one-pound mass at 1 ft/s2, and is equivalent to about 1/32.2 of a pound-force. The slug is defined as the amount of mass that accelerates at 1 ft/s2 when one pound-force is exerted on it, and is equivalent to about 32.2 pounds (mass).
Sensation
The sensation of weight is caused by the force exerted by fluids in the vestibular system, a three-dimensional set of tubes in the inner ear.Sensation of Weight[محل شك] It is actually the sensation of g-force, regardless of whether this is due to being stationary in the presence of gravity, or, if the person is in motion, the result of any other forces acting on the body such as in the case of acceleration or deceleration of a lift, or centrifugal forces when turning sharply.
القياس

Relative weights on the Earth and other celestial bodies
The table below shows comparative gravitational accelerations at the surface of the Sun, the Earth's moon, each of the planets in the solar system. The “surface” is taken to mean the cloud tops of the gas giants (Jupiter, Saturn, Uranus and Neptune). For the Sun, the surface is taken to mean the photosphere. The values in the table have not been de-rated for the centrifugal effect of planet rotation (and cloud-top wind speeds for the gas giants) and therefore, generally speaking, are similar to the actual gravity that would be experienced near the poles.
| Body | Multiple of Earth gravity |
Surface gravity m/s2 |
|---|---|---|
| Sun | 27.90 | 274.1 |
| Mercury | 0.3770 | 3.703 |
| Venus | 0.9032 | 8.872 |
| Earth | 1 (by definition) | 9.8226[16] |
| Moon | 0.1655 | 1.625 |
| Mars | 0.3895 | 3.728 |
| Jupiter | 2.640 | 25.93 |
| Saturn | 1.139 | 11.19 |
| Uranus | 0.917 | 9.01 |
| Neptune | 1.148 | 11.28 |
وحدة قياس الوزن
يقاس الوزن بوحدة دولية تسمى (نيوتن) نسبة إلى العالم الإنجليزي اسحق نيوتن الذي وضع القانون العام للجاذبية، و النيوتن يساوي تقريبا قوة جذب الأرض لكتلة مقدارها 100 جرام.
و فيما يلي بعض المعايير:
- الرطل = 450 جرام
- أوقية = 37.5 جرام
- مثقال = 4.680 جرام ( وزن 65 حبة شعير )
- الدرهم = 3.125 جرام ( وزن 48 شعيرة )
- الحمصة = ربع مثقال
- الجوزة = 4 مثاقيل
- الدانق = 0.525 جرام ( وزن 8 شعيرات )
- القيراط = 0.198 جرام ( وزن 4 شعيرات )
- حبة شعير = 0.049 جرام
- ملعقة الطعام الكبـيرة و هي تعادل وزن مثقال و يعادل وزن 65 حبة شعير تقريباً
- ملعقة الطعام وسـط و هي تعادل نصف مثقال ويعادل وزن 33 حبة شعير تقريبا
- ملعقة الطعام صـغيرة و هي تعادل ربع مثقال ويعادل وزن 17 حبة شعير تقريباً
أمثلة
إذا كانت كتلة الجسم (200) جرام فإن قوة جذب الأرض له تساوي 2 نيوتن. أي أن وزنها = 2 نيوتن و الجسم الذي كتلته (300) جرام فإن وزنه = 3 نيوتن. و إذا كانت كتلة الجسم (1000) جرام أي (1) كجم فإن قوة جذب الأرض له = 10 نيوتن. أي أن وزن الكيلو جرام الواحد على سطح الأرض = 10 نيوتن. و إذا قلنا أن جسما كتلته 2 كجم فإن وزنه = 2 × 10 = 20 نيوتن. و إذا قلنا أن جسما كتلته 5 كجم فإن وزنه = 5 × 10 = 50 نيوتن.
تعريفات
Several definitions exist for weight, not all of which are equivalent.[3][10][11][12]
Gravitational definition
The most common definition of weight found in introductory physics textbooks defines weight as the force exerted on a body by gravity.[1][12] This is often expressed in the formula W = mg, where W is the weight, m the mass of the object, and g gravitational acceleration.
In 1901, the 3rd General Conference on Weights and Measures (CGPM) established this as their official definition of weight:
The word weight denotes a quantity of the same nature[Note 1] as a force: the weight of a body is the product of its mass and the acceleration due to gravity.
This resolution defines weight as a vector, since force is a vector quantity. However, some textbooks also take weight to be a scalar by defining:
The weight W of a body is equal to the magnitude Fg of the gravitational force on the body.[20]
The gravitational acceleration varies from place to place. Sometimes, it is simply taken to have a standard value of 9.80665 m/s2, which gives the standard weight.[18]
The force whose magnitude is equal to mg newtons is also known as the m kilogram weight (which term is abbreviated to kg-wt)[21]
تعريف عملي
In the operational definition, the weight of an object is the force measured by the operation of weighing it, which is the force it exerts on its support.[10] Since W is the downward force on the body by the centre of earth and there is no acceleration in the body, there exists an opposite and equal force by the support on the body. Also it is equal to the force exerted by the body on its support because action and reaction have same numerical value and opposite direction. This can make a considerable difference, depending on the details; for example, an object in free fall exerts little if any force on its support, a situation that is commonly referred to as weightlessness. However, being in free fall does not affect the weight according to the gravitational definition. Therefore, the operational definition is sometimes refined by requiring that the object be at rest.[citation needed] However, this raises the issue of defining "at rest" (usually being at rest with respect to the Earth is implied by using standard gravity).[citation needed] In the operational definition, the weight of an object at rest on the surface of the Earth is lessened by the effect of the centrifugal force from the Earth's rotation.
The operational definition, as usually given, does not explicitly exclude the effects of buoyancy, which reduces the measured weight of an object when it is immersed in a fluid such as air or water. As a result, a floating balloon or an object floating in water might be said to have zero weight.
ISO definition
In the ISO International standard ISO 80000-4:2006,[22] describing the basic physical quantities and units in mechanics as a part of the International standard ISO/IEC 80000, the definition of weight is given as:
Definition
- ,
- where m is mass and g is local acceleration of free fall.
Remarks
- When the reference frame is Earth, this quantity comprises not only the local gravitational force, but also the local centrifugal force due to the rotation of the Earth, a force which varies with latitude.
- The effect of atmospheric buoyancy is excluded in the weight.
- In common parlance, the name "weight" continues to be used where "mass" is meant, but this practice is deprecated.
— ISO 80000-4 (2006)
The definition is dependent on the chosen frame of reference. When the chosen frame is co-moving with the object in question then this definition precisely agrees with the operational definition.[11] If the specified frame is the surface of the Earth, the weight according to the ISO and gravitational definitions differ only by the centrifugal effects due to the rotation of the Earth.
الوزن الظاهر
In many real world situations the act of weighing may produce a result that differs from the ideal value provided by the definition used. This is usually referred to as the apparent weight of the object. A common example of this is the effect of buoyancy, when an object is immersed in a fluid the displacement of the fluid will cause an upward force on the object, making it appear lighter when weighed on a scale.[23] The apparent weight may be similarly affected by levitation and mechanical suspension. When the gravitational definition of weight is used, the operational weight measured by an accelerating scale is often also referred to as the apparent weight.[24]
الكتلة

In modern scientific usage, weight and mass are fundamentally different quantities: mass is an intrinsic property of matter, whereas weight is a force that results from the action of gravity on matter: it measures how strongly the force of gravity pulls on that matter. However, in most practical everyday situations the word "weight" is used when, strictly, "mass" is meant.[8][14] For example, most people would say that an object "weighs one kilogram", even though the kilogram is a unit of mass.
The distinction between mass and weight is unimportant for many practical purposes because the strength of gravity does not vary too much on the surface of the Earth. In a uniform gravitational field, the gravitational force exerted on an object (its weight) is directly proportional to its mass. For example, object A weighs 10 times as much as object B, so therefore the mass of object A is 10 times greater than that of object B. This means that an object's mass can be measured indirectly by its weight, and so, for everyday purposes, weighing (using a weighing scale) is an entirely acceptable way of measuring mass. Similarly, a balance measures mass indirectly by comparing the weight of the measured item to that of an object(s) of known mass. Since the measured item and the comparison mass are in virtually the same location, so experiencing the same gravitational field, the effect of varying gravity does not affect the comparison or the resulting measurement.
The Earth's gravitational field is not uniform but can vary by as much as 0.5%[25] at different locations on Earth (see Earth's gravity). These variations alter the relationship between weight and mass, and must be taken into account in high-precision weight measurements that are intended to indirectly measure mass. Spring scales, which measure local weight, must be calibrated at the location at which the objects will be used to show this standard weight, to be legal for commerce.[citation needed]
This table shows the variation of acceleration due to gravity (and hence the variation of weight) at various locations on the Earth's surface.[26]
| Location | Latitude | m/s2 | Absolute difference from equator | Percentage difference from equator |
|---|---|---|---|---|
| Equator | 0° | 9.7803 | 0.0000 | 0% |
| Sydney | 33°52′ S | 9.7968 | 0.0165 | 0.17% |
| Aberdeen | 57°9′ N | 9.8168 | 0.0365 | 0.37% |
| North Pole | 90° N | 9.8322 | 0.0519 | 0.53% |
The historical use of "weight" for "mass" also persists in some scientific terminology – for example, the chemical terms "atomic weight", "molecular weight", and "formula weight", can still be found rather than the preferred "atomic mass", etc.
In a different gravitational field, for example, on the surface of the Moon, an object can have a significantly different weight than on Earth. The gravity on the surface of the Moon is only about one-sixth as strong as on the surface of the Earth. A one-kilogram mass is still a one-kilogram mass (as mass is an intrinsic property of the object) but the downward force due to gravity, and therefore its weight, is only one-sixth of what the object would have on Earth. So a man of mass 180 pounds weighs only about 30 pounds-force when visiting the Moon.
SI units
In most modern scientific work, physical quantities are measured in SI units. The SI unit of weight is the same as that of force: the newton (N) – a derived unit which can also be expressed in SI base units as kg⋅m/s2 (kilograms times metres per second squared).[14]
In commercial and everyday use, the term "weight" is usually used to mean mass, and the verb "to weigh" means "to determine the mass of" or "to have a mass of". Used in this sense, the proper SI unit is the kilogram (kg).[14]
Pound and other non-SI units
In United States customary units, the pound can be either a unit of force or a unit of mass.[27] Related units used in some distinct, separate subsystems of units include the poundal and the slug. The poundal is defined as the force necessary to accelerate an object of one-pound mass at 1 ft/s2, and is equivalent to about 1/32.2 of a pound-force. The slug is defined as the amount of mass that accelerates at 1 ft/s2 when one pound-force is exerted on it, and is equivalent to about 32.2 pounds (mass).
The kilogram-force is a non-SI unit of force, defined as the force exerted by a one-kilogram mass in standard Earth gravity (equal to 9.80665 newtons exactly). The dyne is the cgs unit of force and is not a part of SI, while weights measured in the cgs unit of mass, the gram, remain a part of SI.
Sensation
The sensation of weight is caused by the force exerted by fluids in the vestibular system, a three-dimensional set of tubes in the inner ear.Sensation of Weight[محل شك] It is actually the sensation of g-force, regardless of whether this is due to being stationary in the presence of gravity, or, if the person is in motion, the result of any other forces acting on the body such as in the case of acceleration or deceleration of a lift, or centrifugal forces when turning sharply.
Measuring

Weight is commonly measured using one of two methods. A spring scale or hydraulic or pneumatic scale measures local weight, the local force of gravity on the object (strictly apparent weight force). Since the local force of gravity can vary by up to 0.5% at different locations, spring scales will measure slightly different weights for the same object (the same mass) at different locations. To standardize weights, scales are always calibrated to read the weight an object would have at a nominal standard gravity of 9.80665 m/s2 (approx. 32.174 ft/s2). However, this calibration is done at the factory. When the scale is moved to another location on Earth, the force of gravity will be different, causing a slight error. So to be highly accurate and legal for commerce, spring scales must be re-calibrated at the location at which they will be used.
A balance on the other hand, compares the weight of an unknown object in one scale pan to the weight of standard masses in the other, using a lever mechanism – a lever-balance. The standard masses are often referred to, non-technically, as "weights". Since any variations in gravity will act equally on the unknown and the known weights, a lever-balance will indicate the same value at any location on Earth. Therefore, balance "weights" are usually calibrated and marked in mass units, so the lever-balance measures mass by comparing the Earth's attraction on the unknown object and standard masses in the scale pans. In the absence of a gravitational field, away from planetary bodies (e.g. space), a lever-balance would not work, but on the Moon, for example, it would give the same reading as on Earth. Some balances are marked in weight units, but since the weights are calibrated at the factory for standard gravity, the balance will measure standard weight, i.e. what the object would weigh at standard gravity, not the actual local force of gravity on the object.
If the actual force of gravity on the object is needed, this can be calculated by multiplying the mass measured by the balance by the acceleration due to gravity – either standard gravity (for everyday work) or the precise local gravity (for precision work). Tables of the gravitational acceleration at different locations can be found on the web.
Gross weight is a term that is generally found in commerce or trade applications, and refers to the total weight of a product and its packaging. Conversely, net weight refers to the weight of the product alone, discounting the weight of its container or packaging; and tare weight is the weight of the packaging alone.
Relative weights on the Earth and other celestial bodies
The table below shows comparative gravitational accelerations at the surface of the Sun, the Earth's moon, each of the planets in the solar system. The "surface" is taken to mean the cloud tops of the gas giants (Jupiter, Saturn, Uranus and Neptune). For the Sun, the surface is taken to mean the photosphere. The values in the table have not been de-rated for the centrifugal effect of planet rotation (and cloud-top wind speeds for the gas giants) and therefore, generally speaking, are similar to the actual gravity that would be experienced near the poles.
| Body | Multiple of Earth gravity |
Surface gravity m/s2 |
|---|---|---|
| Sun | 27.90 | 274.1 |
| Mercury | 0.3770 | 3.703 |
| Venus | 0.9032 | 8.872 |
| Earth | 1 (by definition) | 9.8226[28] |
| Moon | 0.1655 | 1.625 |
| Mars | 0.3895 | 3.728 |
| Jupiter | 2.640 | 25.93 |
| Saturn | 1.139 | 11.19 |
| Uranus | 0.917 | 9.01 |
| Neptune | 1.148 | 11.28 |
القانون
وزن الجسم = كتلة الجسم × وزن الكيلو جرام الواحد
و = ك × ج
| | |
نيوتن كيلو جرام نيوتن / كيلو جرام
انظر أيضاً
- Human body weight
- Tare weight
- weight the English unit
- Weight (object)
ملاحظات
- ^ The phrase "quantity of the same nature" is a literal translation of the French phrase grandeur de la même nature. Although this is an authorized translation, VIM 3 of the International Bureau of Weights and Measures recommends translating grandeurs de même nature as quantities of the same kind.[17]
المراجع
- ^ أ ب ت Richard C. Morrison (1999). "Weight and gravity - the need for consistent definitions". The Physics Teacher. 37 (1): 51. Bibcode:1999PhTea..37...51M. doi:10.1119/1.880152.
- ^ أ ب Igal Galili (2001). "Weight versus gravitational force: historical and educational perspectives". International Journal of Science Education. 23 (10): 1073. Bibcode:2001IJSEd..23.1073G. doi:10.1080/09500690110038585. S2CID 11110675.
- ^ أ ب ت Gat, Uri (1988). "The weight of mass and the mess of weight". In Richard Alan Strehlow (ed.). Standardization of Technical Terminology: Principles and Practice – second volume. ASTM International. pp. 45–48. ISBN 978-0-8031-1183-7.
- ^ Knight, Randall D. (2004). Physics for Scientists and Engineers: a Strategic Approach. San Francisco, USA: Addison–Wesley. pp. 100–101. ISBN 0-8053-8960-1.
- ^ Bauer, Wolfgang and Westfall, Gary D. (2011). University Physics with Modern Physics. New York: McGraw Hill. p. 103. ISBN 978-0-07-336794-1.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Serway, Raymond A. and Jewett, John W. Jr. (2008). Physics for Scientists and Engineers with Modern Physics. USA: Thompson. p. 106. ISBN 978-0-495-11245-7.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Hewitt, Paul G. (2001). Conceptual Physics. USA: Addison–Wesley. pp. 159. ISBN 0-321-05202-1.
- ^ أ ب The National Standard of Canada, CAN/CSA-Z234.1-89 Canadian Metric Practice Guide, January 1989:
- 5.7.3 Considerable confusion exists in the use of the term "weight". In commercial and everyday use, the term "weight" nearly always means mass. In science and technology "weight" has primarily meant a force due to gravity. In scientific and technical work, the term "weight" should be replaced by the term "mass" or "force", depending on the application.
- 5.7.4 The use of the verb "to weigh" meaning "to determine the mass of", e.g., "I weighed this object and determined its mass to be 5 kg," is correct.
- ^ Sur Das (1590s). "Weighing Grain". Baburnama.
- ^ أ ب ت Allen L. King (1963). "Weight and weightlessness". American Journal of Physics. 30: 387. Bibcode:1962AmJPh..30..387K. doi:10.1119/1.1942032. خطأ استشهاد: وسم
<ref>غير صالح؛ الاسم "King" معرف أكثر من مرة بمحتويات مختلفة. - ^ أ ب ت A. P. French (1995). "On weightlessness". American Journal of Physics. 63: 105–106. Bibcode:1995AmJPh..63..105F. doi:10.1119/1.17990. خطأ استشهاد: وسم
<ref>غير صالح؛ الاسم "French" معرف أكثر من مرة بمحتويات مختلفة. - ^ أ ب ت ث Galili, I.; Lehavi, Y. (2003). "The importance of weightlessness and tides in teaching gravitation" (PDF). American Journal of Physics. 71 (11): 1127–1135. Bibcode:2003AmJPh..71.1127G. doi:10.1119/1.1607336.
- ^ Clark, John B (1964). Physical and Mathematical Tables. Oliver and Boyd.
- ^ أ ب ت ث ج A. Thompson & B. N. Taylor (March 3, 2010) [July 2, 2009]. "The NIST Guide for the use of the International System of Units, Section 8: Comments on Some Quantities and Their Units". Special Publication 811. NIST. Retrieved 2010-05-22.
- ^ "Common Conversion Factors, Approximate Conversions from U.S. Customary Measures to Metric". National Institute of Standards and Technology. Retrieved 2013-09-03.
- ^ This value excludes the adjustment for centrifugal force due to Earth’s rotation and is therefore greater than the 9.80665 m/s2 value of standard gravity.
- ^ Working Group 2 of the Joint Committee for Guides in Metrology (JCGM/WG 2) (2008). International vocabulary of metrology – Basic and general concepts and associated terms (VIM) – Vocabulaire international de métrologie – Concepts fondamentaux et généraux et termes associés (VIM) (PDF) (JCGM 200:2008) (in الإنجليزية and الفرنسية) (3rd ed.). BIPM. Note 3 to Section 1.2.
{{cite book}}: CS1 maint: numeric names: authors list (link) - ^ أ ب "Resolution of the 3rd meeting of the CGPM (1901)". BIPM.
- ^ David B. Newell; Eite Tiesinga, eds. (2019). The International System of Units (SI) (PDF) (NIST Special publication 330, 2019 ed.). Gaithersburg, MD: NIST. p. 46.
- ^ Halliday, David; Resnick, Robert; Walker, Jearl (2007). Fundamentals of Physics. Vol. 1 (8th ed.). Wiley. p. 95. ISBN 978-0-470-04473-5.
- ^ Chester, W. Mechanics. George Allen & Unwin. London. 1979. ISBN 0-04-510059-4. Section 3.2 at page 83.
- ^ ISO 80000-4:2006, Quantities and units - Part 4: Mechanics
- ^ Bell, F. (1998). Principles of mechanics and biomechanics. Stanley Thornes Ltd. pp. 174–176. ISBN 978-0-7487-3332-3.
- ^ Galili, Igal (1993). "Weight and gravity: teachers' ambiguity and students' confusion about the concepts". International Journal of Science Education. 15 (2): 149–162. Bibcode:1993IJSEd..15..149G. doi:10.1080/0950069930150204.
- ^ Hodgeman, Charles, ed. (1961). Handbook of Chemistry and Physics (44th ed.). Cleveland, USA: Chemical Rubber Publishing Co. pp. 3480–3485.
- ^ Clark, John B (1964). Physical and Mathematical Tables. Oliver and Boyd.
- ^ "Common Conversion Factors, Approximate Conversions from U.S. Customary Measures to Metric". Nist. National Institute of Standards and Technology. 13 January 2010. Retrieved 2013-09-03.
- ^ This value excludes the adjustment for centrifugal force due to Earth’s rotation and is therefore greater than the 9.80665 m/s2 value of standard gravity.






