أفق

A High desert horizon at sunset, California, USA

The horizon is the apparent line that separates the surface of a celestial body from its sky when viewed from the perspective of an observer on or near the surface of the relevant body. This line divides all viewing directions based on whether it intersects the relevant body's surface or not.

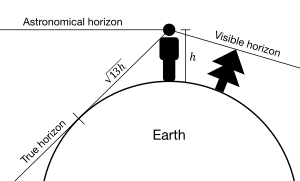
The true horizon is actually a theoretical line, which can only be observed to any degree of accuracy when it lies along a relatively smooth surface such as that of Earth's oceans. At many locations, this line is obscured by terrain, and on Earth it can also be obscured by life forms such as trees and/or human constructs such as buildings. The resulting intersection of such obstructions with the sky is called the visible horizon. On Earth, when looking at a sea from a shore, the part of the sea closest to the horizon is called the offing.^[1]

The true horizon surrounds the observer and it is typically assumed to be a circle, drawn on the surface of a perfectly spherical model of the Earth. Its center is below the observer and below sea level. Its distance from the observer varies from day to day due to atmospheric refraction, which is greatly affected by weather conditions. Also, the higher the observer's eyes are from sea level, the farther away the horizon is from the observer. For instance, in standard atmospheric conditions, for an observer with eye level above sea level by 1.70 متر (5 ft 7 in), the horizon is at a distance of about 5 كيلومتر (3.1 mi).^[2] When observed from very high standpoints, such as a space station, the horizon is much farther away and it encompasses a much larger area of Earth's surface. In this case, the horizon would no longer be a perfect circle, not even a plane curve such as an ellipse, especially when the observer is above the equator, as the Earth's surface can be better modeled as an ellipsoid than as a sphere.

الظهور والاستخدام

View of the ocean with a ship on the horizon (small dot to left of foreground ship)

البعد عن الأفق

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \approx \sqrt{2\,h\,R} \,,}

where h is height above sea level and R is the Earth radius.

When d is measured in kilometres and h in metres, the distance is

d\approx 3.57{\sqrt {h}}\,,

where the constant 3.57 has units of km/m^½.

When d is measured in miles (statute miles i.e. "land miles" of 5،280 أقدام (1،609.344 m)^[2]) and h in feet, the distance is

d\approx {\sqrt {1.5h}}\approx 1.22{\sqrt {h}}\,.

where the constant 1.22 has units of mi/ft^½.

In this equation Earth's surface is assumed to be perfectly spherical, with r equal to about 6،371 كيلومتر (3،959 mi).

أمثلة

Assuming no atmospheric refraction and a spherical Earth with radius R=6،371 كيلومتر (3،959 mi):

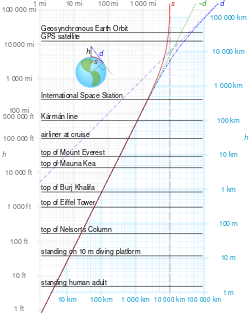
For an observer standing on the ground with h = 1.70 متر (5 ft 7 in), the horizon is at a distance of 4.7 كيلومتر (2.9 mi).
For an observer standing on the ground with h = 2 متر (6 ft 7 in), the horizon is at a distance of 5 كيلومتر (3.1 mi).
For an observer standing on a hill or tower 30 متر (98 ft) above sea level, the horizon is at a distance of 19.6 كيلومتر (12.2 mi).
For an observer standing on a hill or tower 100 متر (330 ft) above sea level, the horizon is at a distance of 36 كيلومتر (22 mi).
For an observer standing on the roof of the Burj Khalifa, 828 متر (2،717 ft) from ground, and about 834 متر (2،736 ft) above sea level, the horizon is at a distance of 103 كيلومتر (64 mi).
For an observer atop Mount Everest (8،848 متر (29،029 ft) in altitude), the horizon is at a distance of 336 كيلومتر (209 mi).
For an observer aboard a commercial passenger plane flying at a typical altitude of 35،000 أقدام (11،000 m), the horizon is at a distance of 369 كيلومتر (229 mi).
For a U-2 pilot, whilst flying at its service ceiling 21،000 متر (69،000 ft), the horizon is at a distance of 517 كيلومتر (321 mi).

كواكب أخرى

Derivation

Geometrical basis for calculating the distance to the horizon, secant tangent theorem

Geometrical distance to the horizon, Pythagorean theorem

Three types of horizon

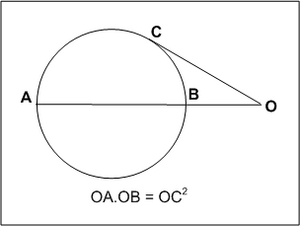
The secant-tangent theorem states that

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{OC}^2 = \mathrm{OA} \times \mathrm{OB} \,.}

Make the following substitutions:

d = OC = distance to the horizon
D = AB = diameter of the Earth
h = OB = height of the observer above sea level
D+h = OA = diameter of the Earth plus height of the observer above sea level,

with d, D, and h all measured in the same units. The formula now becomes

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d^2 = h(D+h)\,\!}

or

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d = \sqrt{h(D+h)} =\sqrt{h(2R+h)}\,,}

where R is the radius of the Earth.

d = distance to the horizon
h = height of the observer above sea level
R = radius of the Earth

referring to the second figure at the right leads to the following:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle (R+h)^2 = R^2 + d^2 \,\!}

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle R^2 + 2Rh + h^2 = R^2 + d^2 \,\!}

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d = \sqrt{h(2R + h)} \,.}

The exact formula above can be expanded as:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d = \sqrt{2Rh + h^2} \,,}

where R is the radius of the Earth (R and h must be in the same units). For example, if a satellite is at a height of 2000 km, the distance to the horizon is 5،430 كيلومتر (3،370 mi); neglecting the second term in parentheses would give a distance of 5،048 كيلومتر (3،137 mi), a 7% error.

التقريب

Graphs of distances to the true horizon on Earth for a given height h. s is along the surface of the Earth, d is the straight line distance, and ~d is the approximate straight line distance assuming h << the radius of the Earth, 6371 km. In the SVG image, hover over a graph to highlight it.

If the observer is close to the surface of the earth, then it is valid to disregard h in the term (2R + h), and the formula becomes-

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d = \sqrt{2Rh} \,.}

Using kilometres for d and R, and metres for h, and taking the radius of the Earth as 6371 km, the distance to the horizon is

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \approx \sqrt{2\cdot6371\cdot{h/1000}} \approx 3.570\sqrt{h} \,} .

Using imperial units, with d and R in statute miles (as commonly used on land), and h in feet, the distance to the horizon is

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \approx \sqrt{2\cdot3963\cdot{h/5280}} \approx \sqrt{1.5h} \approx 1.22 \sqrt{h} } .

If d is in nautical miles, and h in feet, the constant factor is about 1.06, which is close enough to 1 that it is often ignored, giving:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \approx \sqrt h }

If h is significant with respect to R, as with most satellites, then the approximation is no longer valid, and the exact formula is required.

قياسات أخرى

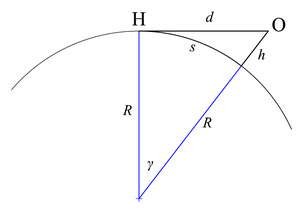
Arc distance

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle s = R \gamma \,;}

then

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos \gamma = \cos\frac{s}{R}=\frac{R}{R+h}\,.}

Solving for s gives

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle s=R\cos^{-1}\frac{R}{R+h} \,.}

The distance s can also be expressed in terms of the line-of-sight distance d; from the second figure at the right,

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan \gamma = \frac {d} {R} \,;}

substituting for γ and rearranging gives

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle s=R\tan^{-1}\frac{d}{R} \,.}

The distances d and s are nearly the same when the height of the object is negligible compared to the radius (that is, h ≪ R).

Zenith angle

Maximum zenith angle for elevated observer in homogeneous spherical atmosphere

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos \gamma =\frac{R}{R+h}}

where خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} is the observer's height above the surface and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} is the angular dip of the horizon. It is related to the horizon zenith angle خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} by:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = \gamma +90{}^\circ }

For a non-negative height خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} , the angle خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} is always ≥ 90°.

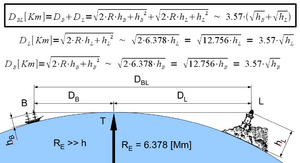
Objects above the horizon

Geometrical horizon distance

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_\mathrm{BL} < 3.57\,(\sqrt{h_\mathrm{B}} + \sqrt{h_\mathrm{L}}) \,,}

where D_BL is in kilometres and h_B and h_L are in metres.

A view across a 20-km-wide bay in the coast of Spain. Note the curvature of the Earth hiding the base of the buildings on the far shore.

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle D \approx 3.57(\sqrt{2}+\sqrt{70})}

which comes to about 35 kilometres.

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3.57 \sqrt{10} }

kilometres from him, which comes to about 11.3 kilometres away. The ship is a further 8.7 km away. The height of a point on the ship that is just visible to the observer is given by:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle h\approx\left(\frac{8.7}{3.57}\right)^2}

which comes to almost exactly six metres. The observer can therefore see that part of the ship that is more than six metres above the level of the water. The part of the ship that is below this height is hidden from him by the curvature of the Earth. In this situation, the ship is said to be hull-down.

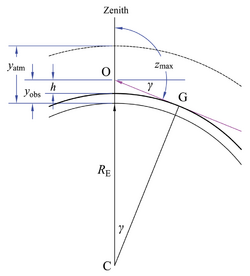
Effect of atmospheric refraction

Typical desert horizon

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d={{R}_{\text{E}}}\left( \psi +\delta \right) \,,}

where R_E is the radius of the Earth, ψ is the dip of the horizon and δ is the refraction of the horizon. The dip is determined fairly simply from

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos \psi = \frac{{R}_{\text{E}}{\mu}_{0}}{\left( {{R}_{\text{E}}}+h \right)\mu } \,,}

where h is the observer's height above the Earth, μ is the index of refraction of air at the observer's height, and μ₀ is the index of refraction of air at Earth's surface.

The refraction must be found by integration of

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta =-\int_{0}^{h}{\tan \phi \frac{\text{d}\mu }{\mu }} \,,}

where خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\,\!} is the angle between the ray and a line through the center of the Earth. The angles ψ and خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi\,\!} are related by

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi =90{}^\circ -\psi \,.}

Simple method—Young

A much simpler approach, which produces essentially the same results as the first-order approximation described above, uses the geometrical model but uses a radius R′ = 7/6 R_E. The distance to the horizon is then^[2]

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d=\sqrt{2 R^\prime h} \,.}

Taking the radius of the Earth as 6371 km, with d in km and h in m,

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \approx 3.86 \sqrt{h} \,;}

with d in mi and h in ft,

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle d \approx 1.32 \sqrt{h} \,.}

Results from Young's method are quite close to those from Sweer's method, and are sufficiently accurate for many purposes.

Curvature of the horizon

The curvature of the horizon is easily seen in this 2008 photograph, taken from a Space Shuttle at an altitude of 226 km (140 mi).

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \kappa=\sqrt{\left(1+\frac{h}{R}\right)^2-1}\ }

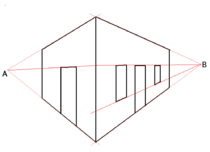
Vanishing points

Two points on the horizon are at the intersections of the lines extending the segments representing the edges of the building in the foreground. The horizon line coincides here with the line at the top of the doors and windows.

انظر أيضاً

References

^ "Offing". Webster's Third New International Dictionary (Unabridged ed.). Pronounced, "Hor-I-zon".
^ ^أ ^ب ^ت خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة ATYoungDistToHoriz