زاوية محوطة

في علم هندسة الرياضيات، فإن الزاوية المحوطة تتشكل من التقاء خطين قاطعين، أو التقاء خط قاطع مخ خط مماس، على دائرة. وبأسلوب مبسط، يمكن القول أن الزاوية المحوطة تتشكل من أي وتري دائرة يتشاركان بنفس نقطة النهاية.

خاصية

ربى ما ضي هه أن قيمة زاوية القوس الذي تشكل بالتقاء خطي زاوية محوطة هي ضعف قيمة الزاوية نفسها.

وهذه الخاصية عدة نتائج منطقية منها:

يمكن برهنة أنه عند التقاء زاويتين محوطتين على نفس القوس، فحصيلة ضرب طول ضلعيهما يكون متساويا.
يمكن برهنة أن الزاويتين المتقابلتين لرباعي دائري هما زاويتان متكاملتان (أي مجموع قيمتهما يساوي 180 درجة).

البرهان

الحالة الأولى: زاوية محوطة بحيث أحد أضلاعها هو قطر الدائرة

أرسم الشكل التالي: أرسم دائرة مركزها نقطة O. أختر نقطتين على محيط الدائرة وسميهم V و A. أرسم الخط VO ومده ليتخطى O ويقطع الدائرة في نقطة B والتي هي مواجهة لنقطة V بالنسبة للمركز. أرسم زاوية ذات رأس V وأضلاعها تمر بـ A و B.

أعطي الزاوية المركزية BOA اسم θ. أرسم خط OA. لاحظ أن خطي OV و OA هما شعاعي الدائرة، لذا هما متساويين. لذلك، فإن المثلث VOA هو متساوي الضلعين وبالتلي، فإن الزاويتين BVA و VAO متساويتان. سمي كل منهما بـ ψ.

بما أن VB هو خطا مستقيما، فإن الزاويتين BOA و AOV هما زاويتين متكاملتين ومجموعهما هو °180. أذا، الزاوية AOV تساوي θ-°180 ومن المعروف أن مجموع زاوية المثلث يساوي °180 فإذا

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi + \psi + 180^\circ - \theta = 180^\circ }

وبالنتيجة

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \psi + 180^\circ - \theta = 180^\circ }

اطرح °180 من الجانبين فتحصل على:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \psi = \theta, \,}

التي تثبت النظرية.

الحالة الثانية: زاوية محوطة بحيث مركز الدائرة بداخلها

ارسم الشكل التالي: ارسم دائرة مركزها O. أختر ثلاث نقط على محيطها وسمهم V و C و D. أرسم الخطين VC و VD.الزاوية DVC هي زاوية محوطة. أرسم الحط VO ومده ليقطع محيط الدائرة في نقطة E لاحظ أن الزاوية DVC تشكل القوس DC على الدائرة..

افترض أن النقطة E هي على هذا القوس. E هي مقابلة للنقطة V. الزاويتين DVE و EVC هما زاويتين محوطتين أيضا وكلاهما لهما ضلع يمر بمركز الدائرة. لذلك الحلو الأولى التي برهنت في الأعلى تنطبق عليهما. فإذن:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle DVC = \angle DVE + \angle EVC. \, }

ودع

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_0 = \angle DVC, }

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_1 = \angle DVE, }

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_2 = \angle EVC, }

بحيث

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_0 = \psi_1 + \psi_2. \qquad \qquad (1) }

أرسم الخطين OC و OD. فتصبح الزاوية DOC زاوية مركزية وكذلك الزاويتين DOE و EOC.

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle DOC = \angle DOE + \angle EOC. }

ودع

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 = \angle DOC, }

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1 = \angle DOE, }

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_2 = \angle EOC, }

بحيث

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 = \theta_1 + \theta_2. \qquad \qquad (2) }

ومن القسم الأول حصلنا على خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1 = 2 \psi_1 } وعلى خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_2 = 2 \psi_2 } . وبدمح النتيجتين مع (2) نحصل على:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 = 2 \psi_1 + 2 \psi_2 \,}

وبالتالي: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 = 2 \psi_0. \,} التي تبرهن النظرية.

الحالة الثالثة: زاوية محوطة بحيث مركز الدائرة خارجها

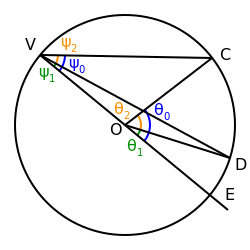
أرسم الشكل التالي: أرسم دائرة مركزه O. أتر ثلاث نقاط V و C و D على محيطها. أرسم الخطين VC و VD. لاحظ أن الزاوية DVC هي زاوية محوطة. ارسم الحط VO ومده بشكل مستقيم ليقطع الدائرة بنقطة E. الزاوية DVC تشكل القوس DC على الدائرة.

أفترض أن نقطة E هي خارج القوس. نقطة E هي متقابلة مع النقطة V. الزاويتين DVE و EVC هما زاويتين محوطتين أيضا ولكلتيهما ضلع يمر بالمركز. فاذا هي مطابقة للحالة الأولى التي برهناها سلفا. لذلك:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle DVC = \angle EVC - \angle DVE } .

دع

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_0 = \angle DVC, }

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_1 = \angle DVE, }

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_2 = \angle EVC, }

بحيث

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi_0 = \psi_2 - \psi_1 \qquad \qquad (3) }

أرسم الخطين OC و OD. الزاوية DOC هي زاوية مركزية و كذلك الزواية: DOE و EOC.

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \angle DOC = \angle EOC - \angle DOE. }

دع

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 = \angle DOC, }

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1 = \angle DOE, }

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_2 = \angle EOC, }

بحيث

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 = \theta_2 - \theta_1 \qquad \qquad (4) }

من القسم الأول حصلنا على:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1 = 2 \psi_1 } و خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_2 = 2 \psi_2 } . وبدمج النتيجة مع (4) نحصل على:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 = 2 \psi_2 - 2 \psi_1 }

اذاً باستعمال (3)

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_0 = 2 \psi_0. }

التي تبرهن النظرية.

وصلات خارجية

مراجع

هذه بذرة مقالة عن الرياضيات تحتاج للنمو والتحسين، ساهم في إثرائها بالمشاركة في تحريرها.