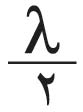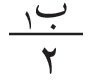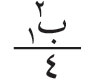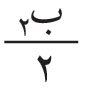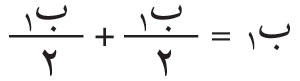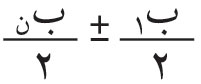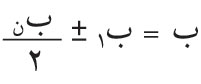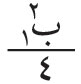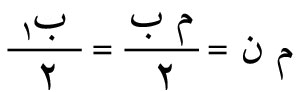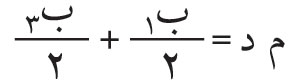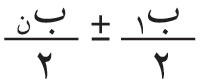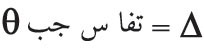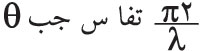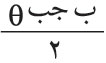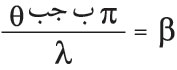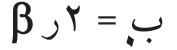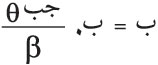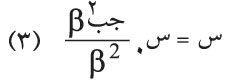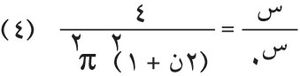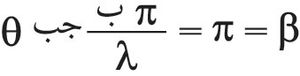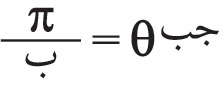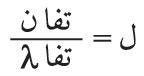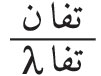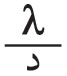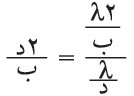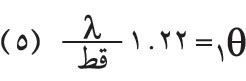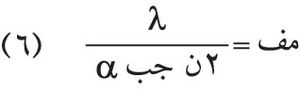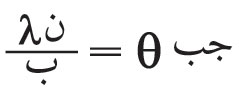حيود

انحراف الضوء أو حيود الضوء(بالإنجليزية : Diffraction) يشير في العادة إلى ظواهر طبيعية عديدة تحدث عند اصطدام موجة (ضوئية أو صوتية)بعائق وتوصف بانها إنحناء شديد الوضوح للموجات حول عوائق صغيرة وانتشار الموجات من خلال فتحات صغيرة.[2] تأثيرات شديدة الشبه تحدث عند حدوث تعاقب في خصائص الوسيط الذي تنتقل به الموجة، على سبيل المثال انحراف قرينة الانكسار لموجات الضوء أو ملف الممانعة الصوتي بالنسبة للموجات الصوتية ويمكن الإشارة لهذه الظواهر بالانحراف الضوئي. يحدث انحراف الضوء مع كل الموجات بما يشمل الموجات الصوتية والموجات الضوئية والموجات الكهرومغناطيسية مثل الضوء المرئي وآشعة أكس وموجات الراديو. وتحدث ظاهرة الحيود أيضا مع الجسيمات الأولية مثل الإلكترون والنيوترون حيث أن الجسيمات الأولية لديها خصائص موجية، فحيود الضوء يحدث أيضا مع المادة ويمكن أن يُدرس طبقاً لميكانيكا الكم.
الانعراج أو الحيود ظاهرة لا ينتشر الضوء من جرائها انتشاراً مستقيماً، بل تنعطف موجاته نحو منطقة الظل الهندسي لحاجزٍ يعترض هذه الموجات.
ويقصد بالظل الهندسي الظلُّ الذي يتكون خلف حاجز معتم وفقاً لنظرية نيوتن في الضوء، التي تنص على أنه جسيمات دقيقة تنتشر في الوسط المتجانس بسرعة كبيرة وفق خطوطٍ مستقيمة، لذلك يطلق عليها «نظرية الانتشار المستقيم». وعلى أساسٍ من ذلك فُسِّر تكوُّن الظل والخسوف والكسوف وتشكل الأخيلة بمختلف الأدوات البصرية[ر]. ولكن إذا أمعن الإنسان النظر في ظل جسم يكوِّنه منبع ضوئي نقطي على حاجز، فإنه يرى أن أطراف الظل غير واضحة الحدود، وأنه تظهر في جوارها مناطق مختلفة الإضاءة، يتوقف توزعها على شكل الجسم وأبعاده. وهذا يدل على أن الضوء لا يستمر على انتشاره المستقيم بعد تخطيه الجسم، بل ينعرج أو يحيد عن مساره المستقيم، لذلك سمِّيت هذه الظاهرة «الانعراج» أو الحيود.
ويحدث حيود الضوء يحدث عند تداخل الموجات الضوئية المنتشرة بعد مرورها من خلال فتحتين أو أكثر، ويلاحظ تأثيراته على وجه الخصوص عندما تكون طول موجة الأشعة مقاربة أومساوية للمسافات بين أنظمة الجسيمات المنحرفة عليها. وتتولد النماذج النظامية نتيجة تداخل الموجات الضوئية فتشتد كثافتها عند نقطة وتقل كثافتها عند أخرى. يتسم تداخل الموجات الضوئية ذات طول موجة واحدة بنوعين من التداخلات. تداخل تتطابق فيه الموجتان بحيث تنطبقان مع بعضهما فيتقابل قمة موجة مع قمة الموجة الأخرى فتشتد شدتهما ويعرف هذا بالتداخل البنـّاء، ويحدث التداخل الثاني بين الشعاعين عندما تتقابل قمة موجة مع قاع للموجة الأخرى فتمحي كل موجة الأخرى وتختفيان. أي لاتظهر لهما صورة. وهذا النوع من التداخل يسمى التداخل الهدام.والنتيجة العامة أن نري صورة النموذج كشكل هندسي، يظهر فيه نقاط شديدة الضوء، ونقاط أخرى لا يأتي الضوء عليها. إنها خاصية موجية. وتشاهد كثيرا مع أنظمة ألبلّورات ويمكن بدراستها تعيين الشكل البلوري للمادن، فمنها ذو بلورة مكعبة ومنها ذو بلورة مسدسة، أو مستطيلة وغيرها.
أمثلة على الحيود في حياتنا اليومية
يمكن مشاهدة حيود الضوء في حياتنا اليومية. من الأمثل المعهودة لحيود (انحراف) الضوء : الأقراص المدمجة (CD & DVD) خيث يوجد بها حزازات (مسارات) دائرية متقاربة وعند سقوط الضوء عليها ينعكس الضوء إلينا في شكل القوس القزح المألوف . وذلك يحدث بسبب حيود الموجات الضوئية عليه حيث أن المسافات بين الحزازات مقاربة لطول الموجات الضوئية . يمكن استغلال هذه الظاهرة في إنتاج حاجز مشبك ذو تصميم مشابه لحزازات القرص يمكن به إنتاج أية انحراف (حيود) موجي مرغوب . الذواكر ثلاثية الأبعاد على كروت الائتمان هي أمثلة على ذلك . الحيود الضوئي يحدث أيضا في الغلاف الجوي حيث تنحرف الأشعة عند اصتدامها بذرات الهواء حول مصدر الضوء يمكنها أن تحدث حلقات لامعة متتالية ضوئية حول مصدر ضوء ساطع كالشمس أو القمر .وتبدو لنا تلك الحلقات حول القمر خصوصا في وجود السحب الخفيفة أو الضباب. يمكن للحيود أن يحدث لأية نوع من الموجات ، موجات البحار يحدث لها حيود (انحراف) حول حواجز الماء والعوائق الأخرى، الموجات الصوتية يمكنها الحيود حول الأشياء ، وهذا سبب استطاعتنا سماع شخص ما بينما نحن خلف حائط على ناصية . الحيود يمكن استخدامه أيضاً في بعض التطبيقات التقنية فهو يضع حدودا أساسية لدرجة نقاء صور الكاميرا والتليسكوب أو الميكروسكوب.
- يستخدم حيود الإلكترونات و حيود الأشعة السينية لتعيين البناء البلوري للمواد . كما يستعمل حيود النيوترونات لتعيين مواقع ذرات الهيدروجين في بلورات المركبات . أي أنها مكملة لحيود اشعة إكس حيث تنعكس أشعة إكس على الذرات الثقيلة وتعين مواقعها في البلورة ، ثم نجري حيود النيوترونات على عينة المركب فتنعكس موجات النيوترونات على ذرات الهيدروجين الخفيفة وتعين أماكنها في البناء البلوري.
- ظاهرة الحيود هي ظاهرة مميزة للموجات سواء كانت موجات مائية أو صوتية أو كهرومغناطيسية أي ضوئية.
وقدرة الإلكترونات و النيوترونات على الحيود على منظومات الذرات تنبع من الخاصية الموجية للإلكترونات والنيوترونات.
تاريخ
التأثير الخاص بحيود الضوء تم رصده بعناية في البدء وتشخيصه من قبل فرانسيسكو ماريا جريمالدي، وهو نفسه من صاغ كلمة(Diffraction) بالأنجليزية من اللاتينية (diffringere) وتعني 'التكسير إلى قطع' إشارة إلى إنكسار الضوء في مناطق شتى. تم نشر نتائج أبحاث جريمالدي بعد وفاته سنة 1665. [3]
فقد لاحظ أنه إذا سقطت حزمة ضوئية ضيقة على ثقب، فإنها لا تكوِّن على حاجز يقع بعده بقعة مضيئة منتظمة تُحدِّدها حافات الثقب، بل تكوِّن سلسلة من حلقات مضيئة تتخللها حلقات ضئيلة الإضاءة. ولم يكن بالمستطاع حينئذ تفسير هذه الظاهرة استناداً إلى نظرية الانتشار المستقيم السائدة، وكان لابد من القول بنظرية أخرى تستطيع تفسير هذه الظواهر، فظهرت النظرية الموجية في الضوء، التي تطوَّرت على يد الهولندي كريسمتيان هويغنز [ر] Huygens، الذي أدخل عليها تحسينات كثيرة، ووضع المبدأ المعروف باسمه، الذي ينص على أن كل نقطة يصل إليها الاضطراب الضوئي يمكن أن تُعدّ منبعاً ثانوياً لاضطراب جديد ينتشر على شكل أمواج كروية ينضم بعضها إلى بعض فيحدِّد مغلِّفها صدر الموجة Wave-front، وهو المحل الهندسي للنقاط التي يصل إليها الاضطراب في وقت واحد فتكون فيه الاهتزازات من ثم متفقة في الطور inphase. وإذا كانت هذه النظرية الموجية قد استطاعت أن تفسّر انعكاس الضوء وانكساره والظواهر الأخرى التي عجزت نظرية نيوتن عن تفسيرها، فإنها لاقت في البدء عقبات في تفسير ظواهر الظلال وغيرها، مما أدى إلى الطعن فيها وإغفالها حينا من الزمن .
شارك إسحق نيوتن في دراسة هذه التأثيرات وعزاها إلى انعطاف شعاع الضوء. جيمس جريجوري لاحظ نموذج من انحراف الضوء على ريشة، والتي كانت بمثابة أول حاجز مشبك لانعطاف الضوء. سنة 1803 قام توماس يونج بتجربة شهيرة حيث لاحظ تداخل موجتين قريبتي التباعد، وقام بتسجيلهم في مقطع طولي، واستنتج أن الضوء ينتشر كموجات.
أجستين جين فريسنل قام بعمل دراسات أكثر دقة وجدية خاصة بحسابات انحراف الضوء. نشرت سنة 1815 وسنة 1818 أعطت دعما كبيرا لنظرية موجات الضوءوالتي طورت بواسطة العالم كريستسان هويجنزو عارضت نظرية نيوتن.
ميكانيكا الانحراف الضوئي
ينشأ الأنحراف الضوئي بسبب طريقة انتشار الموجات، والتي تم شرحها في مبدأ هوجنز، تتصرف كل نقطة من نقاط مقدمة الموجة كمصدر ومركز لموجة جديدة، والسلوك التالي لمقدمة الموجة يحدد بجمع الموجات الصغيرة الصادرة عن نقاط مقدمة الموجة في اللحظة السابقة.[4]
ظواهر الإنعراج
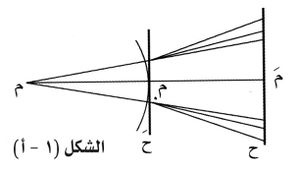
ويمكن التمييز بين صنفين من ظواهر الانعراج، يسمى أحدهما: انعراج فرينل، وفيه يكون ترتيب المنبع الضوئي «م» واللوح «ح» الذي تتكون عليه الظواهر على بعد محدود من الحاجز المعرّج «حَ» كما هو مبين في الشكل (1ـ أ)، وتولّد الظواهرَ حزمٌ متباعدة. ويتميز هذا الانعراج بأنه يسهل فيه الحصول على الظواهر تجريبياً.[1]
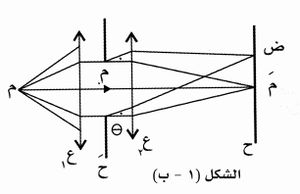
أما الصنف الثاني فهُو انعراج فراونهوفر Fraunhover، وفيه تسقط حزمة متوازية من الضوء على الحاجز، وتُفحص الظواهر المتكوّنة، في المستوي المحرقي لجسمية (ع2) تقع بَعد الحاجز، كما هو مبين في الشكل (1ـ ب) . ويتميز هذا الانعراج ببساطة المعالجة الرياضية وبأهميته العملية.
انعراج فرينل
وهو يشتمل على: تقسيم صدر الموجة إلى مناطق دائرية أو تقسيم صدر الموجة إلى شرائط، ودراسة ظواهر الانعراج باستخدام الطريقة الهندسية أو البيانية:
تقسيم صدر الموجة إلى مناطق دائرية
يمكن تفسير بعض ظواهر الانعراج بتقسيم صدر الموجة إلى مناطق دائرية، يكون مركزها (م0) بمنزلة قطب الموجة بالنسبة إلى النقطة (مَ) انظر الشكل (1ـ أ)، التي تلاحظ عندها ظواهر الانعراج، وتكون أقطار هذه المناطق بحيث تزداد أبعاد محيطاتها عن النقطة (م0) بمقدار
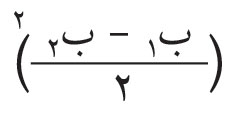
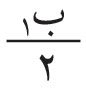
من منطقة إلى التي تليها، حيث λ: طول موجة الضوء الوارد. لذلك تسمى هذه المناطق: «مناطق نصف دورية half-period zones» وتُعرف أيضاً بمناطق فرينل. إن كل نقطة من منطقةٍ ما من هذه المناطق يمكن اعتبارها، وفقاً لمبدأ هويْغنْز، منبعاً ثانوياً تنتشر منه مويجات كروية تسهم في الظواهر المتكونة في النقطة (مَ) وما حولها. ويمكن البرهنة على أن لمناطق فرينل المساحة نفسها على وجه التقريب. وعلى هذا، يمكن القول إن عدد المنابع الثانوية واحد في كل المناطق، أي إن كل منطقة تسهم عند (مَ) بالمقدار نفسه من الطاقة الضوئية. ولكن لما كان بعدُ كل منطقة عن (مَ) يزيد بمقدار على بعد المنطقة التي قبلها، فإن إسهام إحداهما في (مَ) يكون متعاكساً مع إسهام الأخرى لتعاكسهما في الطور (فرق الطور بينهما يساوي π رادياناً أو 180 درجة). ويمكن تمثيل الإسهام الكلي بمجموع متسلسلة من الحدود الموجبة والسالبة المتناوبة، والتي يمثّل كل حدٍ منها إسهامَ منطقة من مناطق فرينل. ولأن ميل المناطق على الحزم الضوئية الصادرة منها نحو (مَ) يتناقص باطراد بدءاً من مركز المناطق، فإن كل حد من حدود المتسلسلة يكون أقل قليلاً من الحد السابق. ويمكن التعبير عن سعة Amplitude محصلة الموجات الواصلة إلى (مَ) بالعلاقة التالية:
ولما كانت القيم المطلقة لحدود هذه المتسلسلة متناقصة، كان مجموعها قيمة محدودة موجبة. ويمكن إثبات أن هذا المجموع يساوي
(انظر البند ـ3)، أي إن سعة محصلة الموجات الواصلة من كامل صدر الموجة إلى (مَ) تساوي نصف سعة الموجة التي تصل إليها من المنطقة الأولى فقط فيما إذا حُجبت كل المناطق الأخرى. ولما كانت شدة الضوء تتناسب مع مربع السعة، فإن شدة الضوء الواصل إلى (مَ) من كامل صدر الموجة تساوي
أي ربع شدة الضوء التي تسهم بها المنطقة الأولى.
وإذا كان في الحاجز الذي تسقط عليه الحزمة الضوئية المتوازية الوحيدة اللون فتحة مستديرة، فإن شدة الضوء في النقطة (مَ)، التي هي مركز ظواهر الانعراج،انظر الشكل (1)، تتوقف على عدد مناطق فرينل التي تغطي هذه الفتحة. فإذا كان قطر الفتحة يساوي قطر منطقة فرينل الأولى، فإن شدة الضوء في (مَ) تساوي (ب21)، أي أربعة أمثال شدته فيما لو لم يكن الحاجز موجوداً. وإذا جُعل قطر الفتحة بحيث يكشف بالنسبة إلى النقطة (مَ) المنطقتين الأولى والثانية معاً، كانت شدة الضوء في (مَ) ضئيلة جداً وتساوي
. وتكون ظواهر الانعراج في هذه الحالة مؤلفة من بقعة مضيئة مركزها مظلم. ويمكن القول، بوجه عام، إن شدة الإضاءة في (مَ) تكون عظمى إذا كُشف من صدر الموجة عدد فردي من المناطق، وتكون صغرى إذا كُشف منه عدد زوجي. وتتألف ظواهر الانعراج بوجه عام من حلقات مضيئة ومظلمة متناوبة.
وإذا استُعمل قرص معتم يحجب المنطقة الأولى فحسب، فإن الإضاءة في النقطة (مَ) لا تكاد تتغير فيما إذا رُفع القرص من طريق الأشعة، فالسعة حين يوضع القرص تساوي
، وهي تكاد تساوي السعة
؛ ويحدث مثل ذلك إذا كان القرص يحجب المنطقة الأولى والثانية أو بضع مناطق أولى، ويكون مركز الظل الهندسي (مَ) بقعة مضيئة تتناقص إضاءتها تناقصاً ضئيلاً بازدياد قطر القرص المعتم.
وإذا استُعمل حاجز مؤلف من مناطق حلقية شفافة ومعتمة متناوبة توافق مناطق فرينل بالنسبة إلى نقطة ما (مَ)، فإن السعة المحصلة فيها تساوي:
حين تكون المناطق الفردية شفافة، أي شدة الإضاءة في (مَ) تكون نسبياً كبيرة جداً، ذلك لأن الموجات الضوئية الواردة من المناطق الفردية الشفافة تصل إلى م0 متفقة جميعاً في الطور. ولا يختلف الأمر عن ذلك فيما إذا كانت المناطق الشفافة هي المناطق الزوجية. ويسمى حاجزٌ كهذا لوح المناطق Zone plate. وهو يكوِّن لمنبع ضوئي نقطي وحيد اللون (ذي تواتر معيّن) خيالاً نقطياً شديد الإضاءة مشابها في ذلك العدسة المقربة، ولكنه يختلف عنها في أنه أشد منها تبديداً Dispersion للضوء الأبيض، إذ يتناسب بعده المحرقي (البؤري) عكساً مع طول الموجة λ، كما يختلف عنها في أنه متعدد المحارق (البؤَر).
في الحالات العملية، تكون أقطار مناطق فرينل صغيرة جداً (من مرتبة الملّيمتر)، لذلك لا تُرى ظواهر الانعراج إلا إذا كانت الحواجز المعتمة أو الفتحات العارجة صغيرة جداً من المرتبة نفسها، كما ترى ظواهر الانعراج في الجوار القريب جداً من أطراف ظلال الحواجز الكبيرة، وفيما عدا ذلك، تختفي ظواهر الانعراج، ولا ترى حينئذ إلا الظواهر التي تنتج من الانتشار المستقيم للضوء (الظِلال والأخيلة التي تكونها العدسات والمرايا للأجسام).
تقسيم صدر الموجة إلى أشرطة
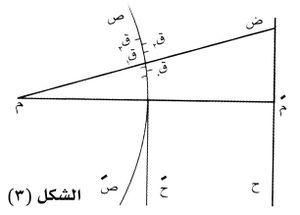
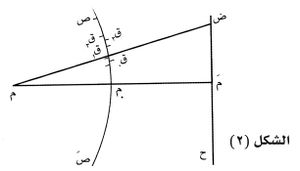
حين يراد دراسة ظواهر الانعراج عند حواجز ذوات حروف مستقيمة (أو عند شق ضيق أو سلك) يضيئها منبع خطي (م) يوازيها، فإن من المناسب تقسيم صدر الموجة الأسطوانية إلى شطريْن، وتقسيم كل شطر إلى أشرطة مستطيلة توازي أطوالها الحرف أو الشق أو السلك المعرِّج. ويعرَّف قطب الموجة (ق0) بالنسبة إلى نقطة ض من اللوح ح، الذي تشاهد عليه ظواهر الانعراج، بأنه نقطة تقاطع المستقيم (ض م) مع صدر الموجة أي (ق0)؛ ويقسم المستوي (م ق0 ص) العمودي على مستوي الشكل صدر الموجة الاسطوانية (ص صَ) إلى شطرين علوي (ق0ص) وسفلي (ق0صَ) (الشكل 2)، ويقسَّم كل من هذين الشطرين إلى أشرطة مستطيلة توازي أطوالها المنبع الخطي م ويكون عرض كل منها بحيث تكون أبعاد أطراف الأشرطة عن النقطة ض، التي يُراد دراسة الظواهر حولها، متزايدة بمقدار من شريط إلى الشريط الذي يليه، أي:
لذلك تسمى هذه الأشرطة أيضاً «أشرطة نصف دورية» وتتصف بالخواص نفسها التي تتصف بها مناطق فرينل نصف الدورية ولكن تختلف عنها في أن مساحاتها ليست متساوية بل تتناقص تناقصاً سريعاً مما يجعل لعامل المساحة في حالة الأشرطة الأثر الأكبر في جعل سعات الاهتزازات الواردة من الأشرطة إلى النقطة ض تتناقص تناقصاً سريعاً حين يبتعد الشريط عن قطب الموجة ق0 بحيث يمكن إهمال فعل الأشرطة البعيدة عن هذا القطب في النقطة (ص) واعتبار الأشرطة القريبة من قطب الموجة ق0 هي الجزء الفعال من هذه الموجة.
لنرمز بالحروف: ب1، ب2، ب3، … إلى سعات الاهتزازات الواصلة إلى (ض) من الأشرطة نصف الدورية الأولى والثانية والثالثة و00 من كل من شطريْ الموجة العلوي والسفلي.
الانعراج عند حرف مستقيم
إن النقطة مَ في (الشكل ـ 3) تمثل حد الظل الهندسي للحاجز المعتم حَ على اللوح (ح)، فإذا كانت (ض) واقعة في منطقة الإضاءة الهندسية بعيدة جداً عن حد الظل الهندسي بحيث ينكشف لها كل الجزء الفعال من الموجة فإنها تكون حينئذ مضاءة كما لو لم يكن الحاجز (حَ) موجوداً،وتكون السعة الحاصلة في (ص) مساوية
وتكون شدة الإضاءة مساوية ب21
وحين تقترب (ض) من حد الظل الهندسي يختفي عنها بعض الأشرطة نصف الدورية الفعالة من الشطر السفلي (ق0صَ) ولا يصل إلى ص حينئذ إلا الاهتزازات الواردة من الشطر العلوي وسعة محصلتها
وإلا الاهتزازات الواردة من الأشرطة المكشوفة من الشطر السفلي وليكن عددها ن، فسعة محصلتها
، وتؤخذ إشارة الجمع عندما يكون ن فردياً وإشارة الطرح عندما يكون زوجياً، أي أن سعة محصلة الاهتزازات الواصلة إلى ص في هذه الحالة تساوي:
أي تتكون في منطقة الإضاءة الهندسية أهداب انعراج تتميز بازدياد شدة الإضاءة في مراكز الأهداب المضيئة لدى الاقتراب من حد الظل الهندسي في حين تتناقص شدة الإضاءة في مراكز الأهداب المظلمة مما يجعل أهداب الانعراج أشد وضوحاً بالقرب من حد الظل الهندسي.
وحين تنطبق (ض) على حد الظل الهندسي يكون المكشوف من صدر الموجة بالنسبة لها هو الشطر العلوي فحسب، فتكون سعة محصلة الاهتزازات الواردة إلى (ض) مساوية
، أي إن شدة الإضاءة تكون
. وإذا ابتعدت ض عن حد الظل داخل هذا الظل بحيث يحتجب عنها الشريط الأول من الشطر العلوي للموجة كانت سعة المحصلة عندها مساوية
، وإذا ابتعدت بحيث يحتجب عنها الشريطان الأول والثاني كانت السعة الحاصلة عندها مساوية ب3/2، وهكذا تتناقص الإضاءة باستمرار في ض كلما ابتعدت عن حد الظل الهندسي فيه حتى إذا وصلت ض إلى موضع يحتجب فيه عنها الجزء الفعال من الشطر العلوي للموجة انعدمت عندها شدة الإضاءة وابتدأ الظل الحقيقي.
دراسة ظواهر الانعراج باستخدام الطريقة الهندسية أو البيانية
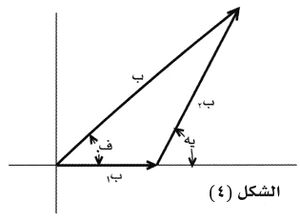
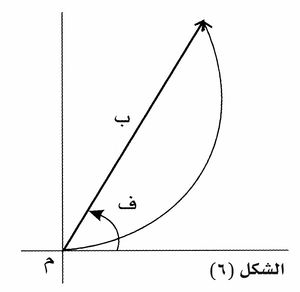
يعتمد مبدأ هذه الطريقة على تمثيل سعة الموجة وطورها حين تصل هذه الموجة إلى نقطةٍ ما بمتجه يتناسب طوله مع سعة الموجة ويساوي ميله طور الموجة. ويبين الشكل (4) متجهين طولاهما ب1 وب2 يوافقان موجتين فرق الطور بينهما (يه).
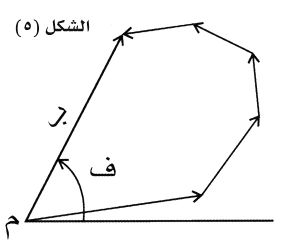
إن سعة المحصلة (ب) وطورها (ف) بالنسبة إلى الموجة الأولى يمكن الحصول عليهما بجمع المتجهين كما هو مبين في الشكل (4). ويمكن البرهنة رياضياً على أن هذه النتيجة صحيحة تماماً، وأنه يمكن تطبيقها في حالة أي عددٍ من الموجات. فإذا كان هناك عدد من الموجات الضوئية الوحيدة اللون فتطبق الطريقة نفسها، ويتكون مضلع كما هو مبين في الشكل (5):
وتكون (ب) سعة محصلة المتجهات كلها. أما عندما يمثِّل عناصر صدر الموجة متجهاتٌ غاية في الصغر، كما ينص مبدأ هويْغنزْ، فإن المضلع ينقلب إلى منحنٍ أملس يسمى منحني الاهتزازة Vibration curve، الممثل في الشكل (6):
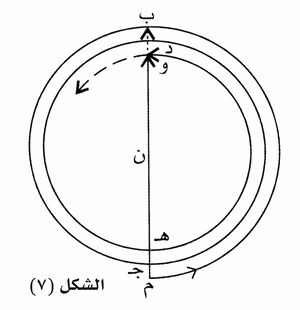
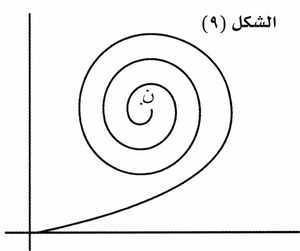
وتطبق الطريقة البيانية هذه لإيضاح إسهامات مناطق فرينل نصف الدورية في توليد ظواهر الانعراج: تُقسم كل منطقة من مناطق فرينل إلى ن منطقة فرعية بالطريقة نفسها التي اتُّبِعت في تقسيم صدر الموجة، فتعطي الطريقة البيانية مضلعاً حلزونياً لتناقص السعات بسبب عامل الميل، وينتهي هذا المضلع إلى منحنٍ حلزوني فيما إذا جُعلت المناطق الفرعية صغيرة صغراً لا نهائياً. ويمثل الشكل (7) جزءاً من منحنٍ حلزوني يبدأ من م وينتهي في مركزه ن.
وتمثل القوس
منطقة فرينل الأولى، لأن فرق الطور بين بدايتها ونهايتها يساوي π رادياناً أو 180 درجة، ويمثّل الطول م ب سعتها ب1. أما القوس فيمثل المنطقة الثانية، كما تمثل القوس المنطقة الثالثة، وهكذا.. فإذا كان كل صدر الموجة مكشوفاً، كانت سعة المحصلة ممثَّلة بالطول
.
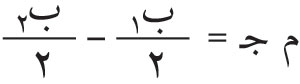
وإذا كُشف من صدر الموجة المنطقتان الأولى والثانية، كانت سعة المحصلة:
وإذا كُشفت المناطق الثلاث الأولى، كانت سعة المحصلة
وهكذا نجد، بوجه عام، أن سعة المحصلة بفعل ن هي منطقة تساوي:
، حيث تؤخذ إشارة الجمع إذا كان ن فردياً، وتؤخذ إشارة الطرح عندما يكون ن زوجياً.
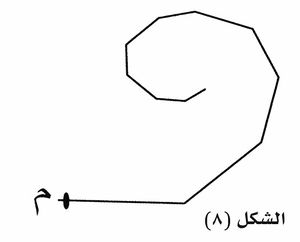
وفي حالة تقسيم صدر الموجة إلى أشرطة نصف دورية، يكون المنحني الحلزوني مختلفاً عن المنحني السابق، وذلك بسبب التناقص السريع في مساحات الأشرطة. ويبين الشكل (8) المضلع الحلزوني في حال عدد محدود من الأشرطة. ويؤول هذا المضلع في النهاية إلى المنحني الحلزوني (الشكل 9) إذا كشف كامل صدر الموجة.
وعندما يقسم صدر الموجة الأسطوانية إلى شطرين، فإن كل شطرٍ منهما يقابله منحن مثل منحني (الشكل ـ9). ومن المناسب رسم هذين المنحنيين في ربعين متقابلين، كما هو مبين في (الشكل ـ10) الذي يمثل كامل الموجة.
وكان أول من ابتكر هذه الطريقة في دراسة ظواهر الانعراج العالم الفرنسي ألفرد كورنو (1841-1902) Cornu، لذلك يسمى الحلزون باسمه «حلزون كورنو». وتمثَّل سعة كامل الموجة على حلزون كورنو بالطول ن نَ. فإذا اعترض الموجة حاجز ذو حرف مستقيم (الشكل ـ 3(، فإن السعة عند طرف الظل الهندسي مَ تمثَّل بالطول م ن، إذ ينحجب عنه أحد شطريْ صدر الموجة. ولدى الابتعاد عن هذا الطرف داخل الظل، تُمثّل السعة بالطول ب ن الذي يتناقص باطراد. وفي منطقة الإضاءة الهندسية (مَ ض)، يكون أحد شطريْ صدر الموجة مكشوفاً كشفاً كاملاً إضافةً إلى عددٍ من أشرطة الشطر الثاني، وتُمثَّل السعة المقابلة لهذه الأشرطة بالطول نَ جـ، حيث تنتقل جـ على لفات الحلزون مقتربة من نَ، فيزداد الطول نَ جـ وينقص بالتناوب كلما ابتعدت ض عن مَ، أي تظهر في منطقة الإضاءة الهندسية أهداب مضيئة وأهداب مظلمة متناوبة يتناقص التباين فيها تناقصاً سريعاً كلما ابتعدت ض عن حد الظل الهندسي كما سبق شرحه.
وفي حال شق ضيق معرِّج، ينكشف من شطريْ صدر الموجة بالنسبة إلى مركز ظواهر الانعراج (مَ)، الشكل (2)، ما يمثِّله القوس ب جـ من الحلزون، ويمثل الطولُ ب جـ السعةَ في مركز الظواهر. ولدى الابتعاد عن هذا المركز، ينزلق الجزء المنحني الثابت الطول ب جـ بحيث يتناقص باطراد وتره الذي يمثل السعة، أي إن شدة الإضاءة تتناقص حتى تنعدم أول مرة عندما يؤلف المنحني ب جـ دائرة واحدة، وهذا يوافق موقع أول هدب مظلم. وتتوالى بعد ذلك أهداب مضيئة متناقصة الإضاءة تفصل بينها أهداب مظلمة. وغني عن البيان أن الظواهر متناظرة بالنسبة إلى مركزها.
وينبغي الإشارة إلى أن مركز الظواهر يمكن أن يكون هدباً مظلماً فيما إذا كان عرض الشق يكشف من صدر الموجة بالنسبة إلى هذا المركز ما يقابل المنحني بَ م جـَ على الحلزون.
انعراج فراوْنْهوفر
يبين الشكل (1ـ ب) سير الأشعة الواردة والأشعة المنعرجة في حالة انعراج فراونهوفر. إن كل نقطة من صدر الموجة المستوية الواصلة إلى مستوى الحاجز العارج يمكن أن تعدّ، وفقاً لمبدأ هويغنز، منبعاً يصدر مويجات ثانوية في كل الاتجاهات، وتتعين ظواهر الانعراج في المستوي المحرقي للعدسة ع2 بتحديد إسهامات هذه المنابع مجتمعة. وتُتَّبع لبلوغ ذلك، طريقة بسيطة هي الطريقة البيانية لإيجاد منحني الاهتزاز (انظر الفقرة3).
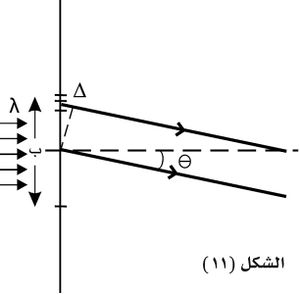
إن منحني الاهتزازة في انعراج فراونهوفر، حين يكون الحاجز المعرَّج شقوقاً ضيقة أطرافها مستقيمة ومتوازية، يؤلف منحنياً دائرياً. فمثلاً، في حالة شق وحيد عرضه (ب) وعمودي على مستوى (الشكل ـ11)، تضيئه ناظمياً حزمة متوازية (موجة مستوية)، يُقسم الشق إلى عددٍ كبير من الأشرطة يساوي عرض كلٍ منها «تفا س».
إن فرق المسير بين الموجتين المنعرجتين بالزاوية θ عند شريطين متجاورين يساوي:
، أي إن فرق الطور بينهما يساوي:
، ولما كانت الشرائط كلها متساوية المساحة، فإن سعات الموجات الصادرة من هذه الأشرطة تكون متساوية أيضاً عند إهمال عامل الميل. وتعطي الطريقة البيانية مضلعا منتظما ينتهي إلى منحنٍ دائري هو منحني الاهتزازة.
ويمكن معرفة توزع الضياء في أهداب انعراج فراونهوفر بدلالة زاوية الانعراج θ كما يلي: إن فرق المسير بين كل من الموجتين المنعرجتين بالزاوية θ عند طرفي الشق وبين الموجة المنعرجة عند مركزه يساوي بالقيمة المطلقة
، ويوافق هذا فرق في الطور يساوي:
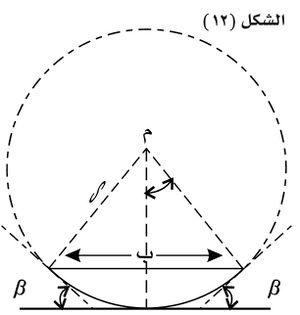
، أي إن المماس عند طرفيْ منحني الاهتزازة يصنع مع الأفقي زاوية مقدارها β، كما هو مبين في (الشكل ـ12) الذي ينتج منه أن السعة ، حيث ر: نصف قطر دائرة منحني الاهتزازة.
أما السعة العظمى ب0 التي تقابل مركز ظواهر الانعراج، حيث تصل كل الموجات متفقة في الطور θ = الصفر)، فهي تساوي طول قوس منحني الاهتزازة، أي إن:
، وينتج إذن
أو
(3)
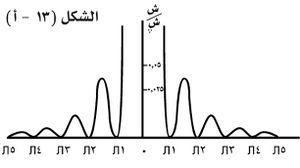
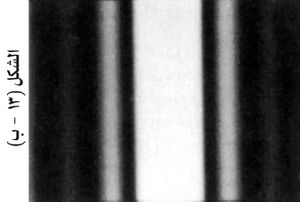
ويبين الشكل (13: أ) الخط البياني الذي يمثل هذه العلاقة، أي توزع الضياء في أهداب الانعراج عند شق ضيق وحيد. ويمكن إثبات أن شدة الضياء في مراكز الأهداب المضيئة الثانوية بالنسبة إلى شدة الضياء في مركز الأهداب تساوي:
حيث ن: رقم الهدب المضيء الثانوي، ويتبين من الشكل (13: ب) أن عرض الهدب المركزي يساوي مثلي عرض أي هدب مضيء ثانوي، وأنه أشد إضاءة في مركزه من الإضاءة في مركز أول هدب مضيء ثانوي بنحو 22 مرة، كما تدل على ذلك العلاقة (4).
ويبين الشكل (13: ج) صورة هذه الأهداب في حالة فتحة دائرية.
ولحساب البعد الهدبي الزاوي بدلالة λ وعرض الشق المعرج ب يُتَّبع ما يلي: إن أول هدب مظلم يوافق
، كما يتبين ذلك من الشكل (13: أ).
أي أن:
. إذن، حين تكون زاوية الانعراج صغيرة، وهي كذلك في معظم الحالات، فإن البعد الهدبي الزاوي يساوي
، والبعد الهدبي الزاوي المركزي يساوي
. فمثلاً، إذا كان λ = 0.5 مكرون (10-6متر)، و ب = 1مم، كان البعد الزاوي للهدب المركزي مساوياً 10-3 راديان، أي نحو 3.5 دقيقة.
ويمكن تصوّر المظاهر الأساسية في انعراج فراونهوفر وتفهمها حين تستخدم حواجز معرجة مختلفة، ويتم ذلك بالاستعانة بمنحني الاهتزازة. فمثلاً، في حال فتحة معرجة مربعة أو مستطيلة، تقسم الفتحة إلى شرائط متساوية موازية لطول الفتحة، وشرائط أخرى متساوية وموازية لعرض الفتحة، فيكون توزع الضياء في كلٍ من هذين المنحنيين المتعامدين كما هو مبين في الشكل (13: أ). ويبين (الشكل ـ14) صورة ظواهر الانعراج عند فتحة مربعة. ويمكن رؤية صورة كهذه إذا نُظر إلى منبع ضوئي شديد بعيد من خلال مظلة مبللة بالمطر أو من خلال نسيج رقيق.
ومن تطبيقات الانعراج عند فتحة مستطيلة حين يكون المنبع الضوئي شقاً ضيقاً، معرفة مقدرة الفصل اللوني للمطياف ذي الموشور، أي مقدرته على التمييز بين خطين طيفيين لضوءين متقاربين جداً في طوليهما الموجيين. وقد وجد أن مقدرة الفصل هذه تساوي:
، حيث ل: طول أطول مسارٍ للضوء في الموشور، و
: تبديد زجاج الموشور، أي تغير قرينة انكساره بتغير طول موجة الضوء.
وحين يكون الحاجز المعرّج مكوناً من شقين عرض كلٍ منهما (ب)، والبعد بين مركزيْهما (د)، تتداخل الموجات المنعرجة عند أحد الشقين مع الموجات المنعرجة عند الشق الآخر مكوِّنةً أهداب تداخل ضمن أهداب الانعراج المضيئة، ويكون البعد الزاوي لأهداب التداخل هذه مساوياً
. وعلى هذا يكون عددها ضمن هدب الانعراج المركزي مساويا:
ويبين (الشكل ـ15:أ) صورة أهداب الانعراج و(الشكل ـ15:ب) صورة أهداب التداخل، ضمن أهداب الانعراج نفسها، وعددها تسعة أهداب ضمن هدب الانعراج المركزي.
وحين يكون حاجز الانعراج فتحة مستديرة، تصبح دراسة الظواهر أشد تعقيداً، ذلك لأنه إذا قُسِّمت الفتحة المستديرة إلى أشرطة متساوية العرض، فإنه لا يكون لها المساحة نفسها وإن كان تغير الطور من شريط إلى آخر مجاورٍ له واحداً؛ فمنحني الاهتزازة في هذه الحالة لا يكون دائريا، فلا تسهل الاستفادة منه للوصول إلى النتيجة على نحو دقيق. ولكن يتوقع المرء أن تكون صورة الانعراج على غرار صورة الانعراج عند فتحة مربعة الشكل، مع الفارق أن الصورة في حالة الفتحة المستديرة تقبل محور تناظر هو المحور العمودي على الفتحة في مركزها، أي أن أهداب الانعراج في هذه الحالة تكون مستديرة تتألف من حلقات مضيئة فمظلمة متناوبة. وتدل الدراسة الرياضية على أن نصف القطر الزاوي لبقعة الانعراج المركزية المضيئة يعطى بالعلاقة:
حيث قط: قطر الفتحة المعرجة.
ومن تطبيقات الانعراج عند فتحة مستديرة تعيين مقدرة الفصل في الآلات البصرية مثل المنظار الفلكي (الراصدة) والمجهر، إذ يتحدد قطر الفتحة المعرجة بقطر إطار جسمية الآلة البصرية أو قطر الحِظار الذي يقع أمام الجسمية.
ففي الراصدة مثلاً، يُصطلح على أنه يمكن بها التمييز بين نجمين إذا وقع مركز بقعة الانعراج العائدة لأحدهما على محيط بقعة الانعراج العائدة للنجم الآخر، أي إن مقدرة الفصل للراصدة تتعين بالعلاقة:
(راديان)، أي تساوي نحو 0.1 ثانية في حالة راصدة قطر جسميتها (80) سنتيمتراً.
أما مقدرة الفصل في المجهر، أي أصغر مسافة بين نقطتين يمكن فصلهما أو تمييزهما بواسطة المجهر، فتعطي اعتماداً على الاصطلاح السابق بما يلي:
حيث ن: قرينة انكسار الوسط الذي يوجد فيه الجسم المفحوص، و α: نصف زاوية الحزمة الضوئية الساقطة على الجسمية، ويدعى الجداء (ن جب α) الفتحة العددية لجسمية المجهر، وهي نحو 1.6 في أفضل المجاهر. وعلى هذا فأصغر قيمة لمقدرة فصل المجهر الضوئي تساوي نحو 0.1 مكرون فيما إذا استُعمل الضوء البنفسجي λ =0.4مكرون.
وتجدر الإشارة هنا إلى أن مقدرة فصل المجهر الالكتروني تخضع إلى العلاقة (6) نفسها، وهي أفضل بآلاف المرات من مقدرة فصل المجهر الضوئي لأن طول موجة الإلكترون قصيرة جداً، فهي من مرتبة الأنجستروم (10-10 متر).
وتنص نظرية بابينِه Babinet على أن ظواهر انعراج فراونهوفر لا تتغير فيما إذا وُضع مكان الفتحة المستديرة قرص معتم له القطر نفسه، أي إنه تتولد حينئذ بقعة انعراج مضيئة في الظل الهندسي للقرص يُعطى نصف قطرها الزاوي بالعلاقة (5) نفسها.
وحين يتكون الحاجز المعرج من عددٍ كبير ن من الفتحات المستديرة أو الأقراص المعتمة المتماثلة قطراً والموزعة توزعا عشوائياً، تتولد ظواهر الانعراج نفسها كما لو كان هناك قرص واحد أو فتحة واحدة، غير أن شدة الضياء في بقعة الانعراج تزداد (ن) مرة. وعلى أساسٍ من هذا تتكون الحلقات الملونة التي تحيط بمصابيح الكهرباء أو مصابيح السيارات بسبب الانعراج عند حبيبات الضباب أو ذرات الغبار الدقيق المتماثلة. وقد وُجد، اعتماداً على العلاقة (5)، أن أقطار حبيبات الضباب تقع بين عشرة وعشرين مكروناً.
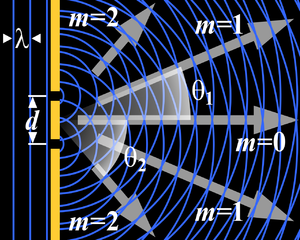
أسهمت ظواهر الانعراج إسهاماً قوياً في دعم النظرية التموجية للضوء، كما كانت مصدر تطبيقات كثيرة أخرى مثل الترشيح الضوئي والهولوغرافية وشبكات الانعراج. وشبكة الانعراج Diffraction grating هي أداة تولّد أطياف الأضواء بالانعراج، وتُستخدم لقياس الأطوال الموجية قياساً دقيقاً. وتتكون بوجه عام من عدد كبير من الحزوز تقابل شقوقاً دقيقة متماثلة متوازية متساوية الأبعاد بعضها عن بعض، وتولد أطياف الضوء المركب في مناحٍ θ تتعين بالعلاقة:
حين تسقط عليها حزمة الضوء المتوازية ناظمياً، حيث ن:هنا مرتبة الطيف (الأول أو الثاني أو 00)، وحيث ب: البعد بين شقين متعاقبين في الشبكة.
اقرأ أيضا
- Atmospheric diffraction
- حيود براگ
- Brocken spectre
- Cloud iridescence
- Diffraction formalism
- Diffraction grating
- Diffraction limit
- Diffractometer
- Dynamical theory of diffraction
- Fraunhofer diffraction
- Fresnel diffraction
- Fresnel imager
- Fresnel number
- Fresnel zone
- موشور
- Powder diffraction
- انكسار (الضوء)
- Schaefer–Bergmann diffraction
- Thinned array curse
- X-ray scattering techniques
- حيود الإلكترونات
- حيود النيوترونات
الهامش والمصادر
- ^ طاهر تريدار. "الانعراج". الموسوعة العربية. Retrieved 2012-04-13.