تراسم قصي
في الهندسة المستوية، التراسم القصي shear mapping، هو خريطة خطية تزيح كل نقطة في اتجاه ثابت، بمقدار يتناسب مع دالة المسافة الخاصة بها من الخط الذي يكون متوازي مع هذا الاتجاه.[1] هذا النوع من التراسم يسمى أيضاً التحويل القصي، transvection، أو ببساطة التراسم.
من أمثلة التراسم، ذلك الذي يأخذ أي نقطة بإحداثيات إلى النقطة . في هذه الحالة، تكون الإزاحة أفقية، الخط الثابت تكون المحور-، والمسافة الموجهة تكون الإحداثيات-. لاحظ أن هذه النقاط تكون على الجوانب المقابلة للخط المرجعي المنزاح في الاتجاهات المقابلة.
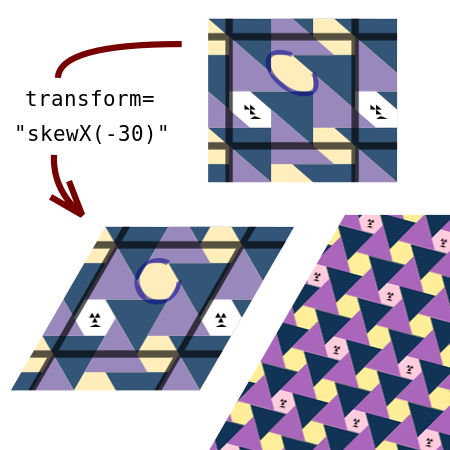
يجب عدم الخلط بين التراسم الخطي والدوران. تطبيق الخريطة القصية على مجموعة من النقاط المسطحة سيغير جميع الزوايا الواقعة بينها (عدا الزوايا المستقيمة)، وطول أي قطعة مستقيمة غير متوازية مع إتجاه الإزاحة. لذلك، فإنها عادة ما تشوه الشكل الهندسي، على سبيل المثال، تحويل المربعات إلى متوازيات أضلاع غير مربعة، والدوائر إلى قطع ناقصة. ومع ذلك يحافظ القص على مساحة الشكل الهندسي، المحاذاة والمسافات النسبية للنقاط الخطية. التراسم القصي هو الفرق الرئيسي بين الأشكال الرأسية والمائلة للحروف.
نفس التعريف يستخدم في الهندسة ثلاثية الأبعاد، عدا تلك المسافة التي يتم قياسها من المسطح الثابت. التحويل القصي ثلاثي الأبعاد يحافظ على حجم الأشكال المصمتة، لكنه يغير مساحات الأشكال المسطحة (عدا تلك التي تكون متوازية مع الإزاحة).
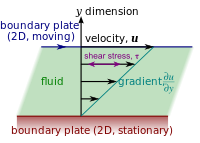
يستخدم هذا التحويل لوصف التدفق الصفيحي للموائع بين الصفائح المتوازية، عند تحركها في المسطح العلوي والمتوازي مع الأول.
التعريف
التراسم الأفقي والرأسي للمسطح
التراسم القصي العام
التطبيقات
المصادر
- Weisstein, Eric W. "Shear" from Mathworld, A Wolfram Web Resource.