متباينة (رياضيات)

هذا المقال هو عن relations "greater than" and "less than". إذا كنت تريد the relation "not equal"، انظر Inequation.

"Less than" و "Greater than" يـُحوّلا إلى هنا. للاستخدامات الأخرى, انظر [[the symbol < (توضيح)]].

لمعلومات عن the UK insurance brand "More TH>N"، انظر More Than (company).

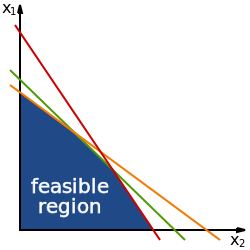
في الرياضيات، التباين inequality هي علاقة تقوم بمقارنة غير متساوية بين رقمين أو تعبيرين رياضيين أخريين. يتم استخدامه غالبًا لمقارنة رقمين على مستقيم الأعداد حسب حجمهما. هناك العديد من الرموز المختلفة المستخدمة لتمثيل أنواع مختلفة من التباين:

• الرمز a < b يعني أن a أصغر من b.
• الرمز a > b يعني أن a أكبر من b.

يتم تعريف المنطقة المجدية من البرمجة الخطية من خلال مجموعة من المتباينات.

في كلتا الحالتين، a لا يساوي b. تُعرف هذه العلاقات باسم تباين (عدم مساواة) تام,يعني ذلك a أصغر تمامًا من b أو أكبر منه تمامًا. أما التساوي فهو مستبعد.

على النقيض من التباين التام، هناك نوعان من علاقات التباين غير التام:

• الإشارة a ≤ b أو a ⩽ b يعني أن a أصغر أو يساوي b (أو، بشكل مساوي على الأكثر لb، أو ليست أكبر من b).
• الإشارة a ≥ b أو a ⩾ b يعني أن a أكبر أو يساوي b (أو، بشكل مساوي على الأقل لb، أ, ليست أصغر من b).

يمكن أيضًا تمثيل العلاقة "ليس أكبر من" a ≯ b، رمز "أكبر من" مقسم بشطب مائل، "لا". وينطبق الشيء نفسه على "ليس أقل من" و a ≮ b.

تعني الإشارة a ≠ b أن a غير مساوي ل b، ويعتبر أحيانًا شكلاً من أشكال التباين التام.لا يقال أن أحدهما أكبر من الآخر؛ لا يتطلب حتى a و b أن تكون عضوًا في مجموعة منتظمة.

في العلوم الهندسية، أقل استخدام رسمي لمجموعة الإشارات هو ذكر أن كمية واحدة "أكبر بكثير" من أخرى، عادةً بعدة ترتيبات من حيث الحجم. وهذا يعني أنه يمكن إهمال القيمة الأقل مع تأثير ضئيل على دقة التقريب (مثل حالة حدود النسبية الفائقة في الفيزياء).

• الإشارة a ≪ b يعني أن a أقل بكثير من b. (في نظرية القياس، ومع ذلك، يتم استخدام هذا الترميز لـ الاستمرارية المطلقة، وهو مفهوم غير مرتبط بذلك.)
• الإشارة a ≫ b يعني أن a أكبر بكثير من b.

في جميع الحالات المذكورة أعلاه، فإن أي رمزين يعكسان بعضهما البعض يكونان متناسبين؛ أي تكون الإشارات a < b و b > a متكافئة، إلخ.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الخصائص على مستقيم الأعداد

المتباينات تحكمها الخصائص. كل هذه الخصائص تنطبق أيضًا إذا تم استبدال جميع المتباينات غير التامة (≤ و ≥) بالتباينات التامة المقابلة لها (< و >) و - في حالة تطبيق دالة - تقتصر التوابع المستمرة على التابع المستمر "بشكل تام".

 العكس

العلاقات ≤ و ≥ هي عكسية، وهذا يعني أنه لأي عدد حقيقي a و b:

a ≤ b و b ≥ a متكافئان.

 الانتقالية

تنص الخاصية الانتقالية للتباين أنه لأي عدد حقيقي a، b، c:

إذا a ≤ b و b ≤ c، إذاً a ≤ c.

إذا كان أياً من المقدمات المنطقية عبارة عن تباين تام، فإن الاستنتاج هو تباين تام:

إذا a ≤ b و b < c، إذاً a < c.

إذا a < b و b ≤ c، إذاً a < c.

 الجمع والطرح

إذا x < y، إذاً x + a < y + a.

الثابت المشترك c قد تكون المضاف أو المطروح من كلا جانبي المتباينة. لذلك، لأي من الأعداد الحقيقية a، b، c:

إذا a ≤ b، إذاً a + c ≤ b + c و a − c ≤ b − c.

بمعنى آخر، يتم الاحتفاظ بعلاقة التباين تحت الجمع (أو الطرح) والأعداد الحقيقية هي مجموعة منتظمة مع الإضافة.

 الضرب و القسمة

إذا x < y و a > 0، إذاً ax < ay.

إذا x < y و a < 0، إذاً ax > ay.

تشير الخصائص التي تتعامل مع الضرب و القسمة إلى أنه لأي عدد حقيقي، a، b و c غير صفري:

إذا a ≤ b و c > 0، إذاً ac ≤ bc و a/c ≤ b/c.

إذا a ≤ b وc < 0، إذاً ac ≥ bc و a/c ≥ b/c.

بمعنى آخر، يتم الحفاظ على علاقة التباين في ظل الضرب والقسمة بثابت موجب، ولكن يتم عكسها عندما يتعلق الأمر بثابت سالب. بشكل عام، ينطبق هذا على مجال منتظم. لمزيد من المعلومات، راجع المجالات المنتظمة.

 عكس الجمع

تنص خاصية عكس الجمع لأي من الأعداد الحقيقية a و b:

إذا a ≤ b، إذاً −a ≥ −b.

 عكس الضرب

إذا كان كلا العددين موجبين، فإن علاقة التباين بين عكس الضرب تكون معاكسة لتلك الموجودة بين الأعداد الأصلية. وبشكل أكثر تحديدًا، لأي عدد حقيقي غير صفري a و b وكلاهما موجب (أو كلاهما سلبي):

إذا a ≤ b، إذاً 1/a ≥ 1/b.

يمكن أيضًا كتابة جميع الحالات الخاصة التأشير المتسلسل بإشارات a و b، كما يلي:

إذا 0 < a ≤ b، إذاً 1/a ≥ 1/b > 0.

إذا a ≤ b < 0، إذاً 0 > 1/a ≥ 1/b.

إذا a < 0 < b، إذاً 1/a < 0 < 1/b.

 تطبيق دالة على جانبي المتباينة

رسم بياني ل y = ln x

أي تابع متزايد بشكل تراتبي (مستمر)، حسب تعريفها،يمكن تطبيقه على كلا جانبي المتباينة دون كسر علاقة عدم التباين (بشرط أن يكون كلا التعبيرين في المجال الخاص لذلك التابع). ومع ذلك، فإن تطبيق دالة متناقصة بشكل تراتبي (مستمر) على جانبي المتباينة يعني أن علاقة عدم المساواة ستنعكس. قواعد عكس الجمع، عكس الضرب للأعداد الموجبة، كلاهما مثالان لتطبيق دالة متناقصة بشكل تراتبي (مستمر).

إذا كانت المتباينة (a < b، a > b) تامة و يكون التابع مستمر تمامًا، فتبقى المتباينة تامة. إذا كان شرط واحد فقط من هذه الشروط تاماً، فإن المتباينة الناتجة تكون غير تامة. في الواقع، تعتبر قواعد العكس الإضافية والمضاعفة مثالين على تطبيق دالة متناقصة مستمرة تامة.

بعض الأمثلة على هذه القاعدة هي:

• رفع كلا جانبي المتباينة إلى قوة n > 0 (equiv.، −n < 0)، عندما a و b أعداد حقيقية موجبة:

0 ≤ a ≤ b ⇔ 0 ≤ aⁿ ≤ bⁿ.

0 ≤ a ≤ b ⇔ a⁻ⁿ ≥ b⁻ⁿ ≥ 0.

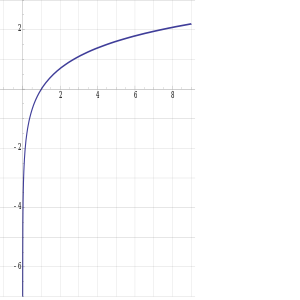
• أخذ اللوگاريتم الطبيعي على جانبي المتباينة، عندما a و b أعداد حقيقية موجبة:

0 < a ≤ b ⇔ ln(a) ≤ ln(b).

0 < a < b ⇔ ln(a) < ln(b).

(هذا صحيح لأن اللوگاريتم الطبيعي هو دالة متزايدة بشكل تام.)

 تعاريف و قوانين عامة اصطلاحية

التنظيم الجزئي (غير التام) هو علاقة ثنائية ≤ خلال مجموعة P وهي انعكاسية، غير متماثلة، و متعدية. وهذا، لجميع a و b وc في P، يجب أن تفي بالبنود الثلاثة التالية:

1. a ≤ a ( انعكاسية)
2. إذا a ≤ b و b ≤ a، إذاً a = b ( غير متماثلة)
3. إذا a ≤ b و b ≤ c، إذاً a ≤ c ( متعدية)

تسمى المجموعة ذات التنظيم الجزئي مجموعة منظمة جزئياً. هذه هي الحقائق الأساسية التي يجب أن يحققها كل نوع من الأنظمة. تشمل الحقائق الأخرى الموجودة للتعريفات الأخرى للتنظيمات على مجموعة P ما يلي:

1. لكل a و b في P، a ≤ b أو b ≤ a (تنظيم كلي).
2. لكل a و b في P لأي a < b، يوجد c في P حيث أن a < c < b (تنظيم مركز).
3. كل مجموعة فرعية غير فارغة من P ذات الحد الأعلى لها الحد الأعلى الأصغري (أعلى) في P (خاصية الحد الأعلى - الأصغري).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 المجالات المنتظمة

المقالة الرئيسية: Ordered field

إذا (F، +، ×) هو مجال و ≤ منتظم كاملاً على F، عندها تسمى (F، +، ×، ≤) مجال منتظم إذا وفقط إذا:

• a ≤ b تفترض a + c ≤ b + c;
• 0 ≤ a و 0 ≤ b تفترض 0 ≤ a × b.

كل من (Q, +, ×, ≤) و (R، +، ×، ≤) مجالات منتظمة، لكن ≤ لا يمكن تعريفه من أجل جعل (C، +، ×، ≤) مجال منتظم لأن −1 هو مربع i وبالتالي سيكون موجبًا.

بالإضافة إلى كونه مجالاً منتظماً، فإن R لها أيضًا خاصية الحد الأعلى الأصغري. في الواقع، يمكن تعريف R على أنه المجال الوحيد المنتظم بهذه الجودة.

 تأشير متسلسل

يرمز التأشير a < b < c إلى "a < b and b < c"، والتي من خلالها، عن طريق الخاصية المتعدية أعلاه، يتبع ذلك أيضًا a < c.بموجب القوانين المذكورة أعلاه، يمكن للمرء أن يجمع أو يطرح نفس العدد لجميع الحدود الثلاثة، أو يضرب أو يقسم جميع الحدود الثلاثة على نفس العدد غير الصفري وعكس جميع المتباينات إذا كان هذا الرقم سالبًا. ومن ثم، على سبيل المثال، a < b + e < c تعادل a − e < b < c − e.

يمكن تعميم هذا التأشير على أي عدد من المصطلحات: على سبيل المثال، a₁ ≤ a₂ ≤ ... ≤ a_n يعني a_i ≤ a_i+1 for i = 1, 2, ..., n − 1. عن طريق الخاصية المتعدية، تعادل هذه الحالة a_i ≤ a_j for any 1 ≤ i ≤ j ≤ n.

عند حل المتباينات باستخدام التأشير المتسلسل، من الممكن والضروري أحيانًا تقييم المصطلحات بشكل مستقل. على سبيل المثال، لحل المتباينة 4x < 2x + 1 ≤ 3x + 2، لا يمكن عزلx في أي جزء من المتباينة من خلال الجمع أو الطرح. بدلاً من ذلك، يجب حل المتباينات بشكل مستقل، وتحقيق النتائج المطلوبة x < 1/2 و x ≥ −1 على التوالي، والتي يمكن دمجها في الحل النهائي −1 ≤ x < 1/2.

من حين لآخر، يتم استخدام التأشير المتسلسل مع المتباينات في اتجاهات مختلفة، وفي هذه الحالة يكون المعنى هو التوحيد المنطقي للمتباينات بين المصطلحات المتقاربة. على سبيل المثال، يتم كتابة الشرط المحدد لـ الوضع المتعرج على شكل a₁ < a₂ > a₃ < a₄ > a₅ < a₆ > ... . يتم استخدام التأشير المتسلسل المختلط في كثير من الأحيان مع العلاقات المتوافقة، مثل <, =, ≤. على سبيل المثال، a < b = c ≤ d يعني a < b، b = c، وc ≤ d. هذا التأشير موجود في عدد قليل من لغات البرمجة مثل پايثون. في المقابل، في لغات البرمجة التي تقدم ترتيبًا لنوع نتائج المقارنة، مثل C، حتى السلاسل المتجانسة قد يكون لها معنى مختلف تمامًا.

 متباينات حادة

يقال إن المتباينة حادة، إذا كان لا يمكن تخفيفها ولا تزال صحيحة بشكل عام. اصطلاحياً، تسمى المتباينة المكممة دائماً φ حادة إذا، لكل متباينة كمية تامة صحيحةψ، إذا استمرت ψ ⇒ φ، إذاً استمرت أيضاً ψ ⇔ φ . على سبيل المثال، تكون المتباينة ∀a ∈ ℝ. a² ≥ 0 حادة، بينما تكون المتباينة ∀a ∈ ℝ. a² ≥ −1 غير حادة.

 المتباينات بين الأوساط

انظر أيضاً: المتباينات في الأوساط الحسابية والهندسية

هناك العديد من المتباينات بين الأوساط. على سبيل المثال، لأي من الأعداد الموجبة a₁, a₂, …, a_n لدينا H ≤ G ≤ A ≤ Q, حيث

$H={\frac {n}{{\frac {1}{a_{1}}}+{\frac {1}{a_{2}}}+\cdots +{\frac {1}{a_{n}}}}}$	(الوسط التوافقي),
$G={\sqrt[{n}]{a_{1}\cdot a_{2}\cdots a_{n}}}$	(الوسط الهندسي),
$A={\frac {a_{1}+a_{2}+\cdots +a_{n}}{n}}$	(المتوسط الحسابي),
$Q={\sqrt {\frac {a_{1}^{2}+a_{2}^{2}+\cdots +a_{n}^{2}}{n}}}$	(الوسط التربيعي).

 متباينة كوشي-شوارتز

انظر أيضاً: متباينة كوشي-شوارتز

تنص متباينة كوشي-شوارتز على أن جميع المتجهات u و v من مجال الناتج الداخلي صحيحة

$|\langle \mathbf {u} ,\mathbf {v} \rangle |^{2}\leq \langle \mathbf {u} ,\mathbf {u} \rangle \cdot \langle \mathbf {v} ,\mathbf {v} \rangle ,$

حيث $\langle \cdot ,\cdot \rangle$ هو الناتج الداخلي. تتضمن أمثلة النواتج الداخلية الناتج النقطي الحقيقي والعقدي؛ في المجال الإقليدي Rⁿ مع الناتج الداخلي القياسي، تكون متباينة كوشي-شوارتز

$\left(\sum _{i=1}^{n}u_{i}v_{i}\right)^{2}\leq \left(\sum _{i=1}^{n}u_{i}^{2}\right)\left(\sum _{i=1}^{n}v_{i}^{2}\right).$

 متباينات أسية

"المتباينة الأسية" هي متباينة تحتوي على مصطلحات من النموذج a^b، حيث a و b هي أرقام موجبة حقيقية أو تعبيرات متغيرة. غالبًا ما تظهر في تمارين أولمپياد الرياضية.

 أمثلة

• لأي عدد حقيقي x,

$e^{x}\geq 1+x.$

• إذا x > 0 و p > 0، إذاً

${\frac {x^{p}-1}{p}}\geq \ln(x)\geq {\frac {1-{\frac {1}{x^{p}}}}{p}}.$

في نهاية p → 0، تلتقي الحدود العلوية والسفلية ln(x).

• إذا x > 0، إذاً

$x^{x}\geq \left({\frac {1}{e}}\right)^{\frac {1}{e}}.$

• إذا x > 0، إذاً

$x^{x^{x}}\geq x.$

• إذا x، y، z > 0، إذاً

$\left(x+y\right)^{z}+\left(x+z\right)^{y}+\left(y+z\right)^{x}>2.$

• لأي من الأعداد المميزة a و b,

${\frac {e^{b}-e^{a}}{b-a}}>e^{(a+b)/2}.$

• إذا x، y > 0 و 0 < p < 1، إذاً

$x^{p}+y^{p}>\left(x+y\right)^{p}.$

• إذا x، y، z > 0، إذاً

$x^{x}y^{y}z^{z}\geq \left(xyz\right)^{(x+y+z)/3}.$

• إذا a، b > 0، إذاً

$a^{a}+b^{b}\geq a^{b}+b^{a}.$

• إذا a، b > 0، إذاً

$a^{ea}+b^{eb}\geq a^{eb}+b^{ea}.$

• إذا a، b، c > 0، إذاً

$a^{2a}+b^{2b}+c^{2c}\geq a^{2b}+b^{2c}+c^{2a}.$

• إذا a، b > 0، إذاً

$a^{b}+b^{a}>1.$

 المتباينات الشهيرة

انظر أيضاً: قائمة المتباينات

غالبًا ما يستخدم علماء الرياضيات المتباينات للكميات المحدودة التي لا يمكن حساب الصيغ الدقيقة لها بسهولة. يتم استخدام بعض أشكال المتباينات في كثير من الأحيان بحيث يكون لها أسماء:

• Azuma's inequality
• Bernoulli's inequality
• Bell's inequality
• Boole's inequality
• Cauchy–Schwarz inequality
• Chebyshev's inequality
• Chernoff's inequality
• Cramér–Rao inequality
• Hoeffding's inequality
• Hölder's inequality
• Inequality of arithmetic and geometric means
• Jensen's inequality
• Kolmogorov's inequality
• Markov's inequality
• Minkowski inequality
• Nesbitt's inequality
• Pedoe's inequality
• Poincaré inequality
• Samuelson's inequality
• Triangle inequality

 الأعداد العقدية والمتباينات

مجموعة الأعداد العقدية ℂ مع عملياتها الجمع و الضرب هي مجال، لكن من المستحيل تحديد أي علاقة ≤ بحيث تصبح (ℂ, +, ×, ≤) مجالاً منتظماً. لجعل (ℂ, +, ×, ≤) حقلاً منظماً، يجب أن تحقق الخاصيتين التاليتين:

• إذا a ≤ b، إذاً a + c ≤ b + c;
• إذا 0 ≤ a و 0 ≤ b، إذاً 0 ≤ ab.

لأن ≤ هو الترتيب الإجمالي، لأي عدد a، إما 0 ≤ a أو a ≤ 0 (في هذه الحالة ، تشير الخاصية الأولى أعلاه إلى ذلك 0 ≤ −a). في كلتا الحالتين 0 ≤ a²;هذا يعني أن i² > 0 و 1² > 0;لذلك −1 > 0 و 1 > 0، مما يعني تعارض (−1 + 1) > 0.

ومع ذلك، يمكن تعريف العملية ≤ بحيث تحقق الخاصية الأولى فقط (اصطلاحاً، "إذا a ≤ b، إذاً a + c ≤ b + c"). في بعض الأحيان يتم استخدام تعريف الترتيب المعجمي:

• a ≤ b، إذا
  • Re(a) < Re(b)، أو
  • Re(a) = Re(b) و Im(a) ≤ Im(b)

يمكن بسهولة إثبات ذلك لهذا التعريف a ≤ b مما يشير إلى a + c ≤ b + c.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 متباينات المتجهات

يمكن أيضًا تعريف علاقات المتباينات المشابهة لتلك المحددة أعلاه لـ متجه عمودي. إذا جعلنا المتجهات $x,y\in \mathbb {R} ^{n}$ (مما يعني $x=(x_{1},x_{2},\ldots ,x_{n})^{\mathsf {T}}$ و $y=(y_{1},y_{2},\ldots ,y_{n})^{\mathsf {T}}$، حيث $x_{i}$ و $y_{i}$ أعداد حقيقية على كل $i=1,\ldots ,n$)، يمكننا تعريف العلاقات التالية:

• $x=y$، إذا $x_{i}=y_{i}$ على كل $i=1,\ldots ,n$.
• $x<y$، إذا $x_{i}<y_{i}$ على كل $i=1,\ldots ,n$.
• $x\leq y$, إذا $x_{i}\leq y_{i}$ على كل $i=1,\ldots ,n$ و $x\neq y$.
• $x\leqq y$، إذا $x_{i}\leq y_{i}$ على كل $i=1,\ldots ,n$.

وبالمثل ، يمكننا تعريف العلاقات لـ $x>y$، $x\geq y$، و $x\geqq y$. يتوافق هذا التأشير مع ما استخدمه ماتياس إيرگوت في تحسين متعدد المعايير Multicriteria Optimization (انظر المراجع).

خاصية ثلاثية الأجزاء (كما هو مذكور أعلاه) غير صالحة لعلاقات المتجهات. على سبيل المثال، عندما $x=(2,5)^{\mathsf {T}}$ و $y=(3,4)^{\mathsf {T}}$، لا توجد علاقة تباين صحيحة بين هذين المتجهين. أيضًا، يجب تحديد العكس المضاعف على المتجه قبل النظر في هذه الخاصية. ومع ذلك، بالنسبة لبقية الخصائص المذكورة أعلاه، توجد خاصية موازية للمتباينات المتجهة.

 أنظمة المتباينات

يمكن تبسيط أنظمة المتباينات الخطية عن طريق استبعاد فورييه - موتسكين.

التحلل الجبري الأسطواني عبارة عن خوارزمية تسمح باختبار ما إذا كان لنظام المعادلات المتعددة الحدود والمتباينات حلول، وإذا وجدت الحلول، يتم وصفها. تعقيد هذه الخوارزمية هو مضاعف أسي في عدد المتغيرات. فهو مجال بحث نشط لتصميم خوارزميات أكثر كفاءة في حالات محددة.

 انظر أيضاً

• Binary relation
• Bracket (mathematics), for the use of similar ‹ and › signs as brackets
• Inclusion (set theory)
• Inequation
• Interval (mathematics)
• List of inequalities
• List of triangle inequalities
• Partially ordered set
• Relational operators, used in programming languages to denote inequality

 المصادر

• Hardy, G., Littlewood J. E., Pólya, G. (1999). Inequalities. Cambridge Mathematical Library, Cambridge University Press. ISBN 0-521-05206-8.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Beckenbach, E. F., Bellman, R. (1975). An Introduction to Inequalities. Random House Inc. ISBN 0-394-01559-2.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Drachman, Byron C., Cloud, Michael J. (1998). Inequalities: With Applications to Engineering. Springer-Verlag. ISBN 0-387-98404-6.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Grinshpan, A. Z. (2005), "General inequalities, consequences, and applications", Advances in Applied Mathematics 34 (1): 71–100, doi:10.1016/j.aam.2004.05.001 
• Murray S. Klamkin. "'Quickie' inequalities" (PDF). Math Strategies.
• Arthur Lohwater (1982). "Introduction to Inequalities". Online e-book in PDF format.
• Harold Shapiro (2005). "Mathematical Problem Solving". The Old Problem Seminar. Kungliga Tekniska högskolan.
• "3rd USAMO". Archived from the original on 2008-02-03.
• Pachpatte, B. G. (2005). Mathematical Inequalities. North-Holland Mathematical Library. Vol. 67 (first ed.). Amsterdam, The Netherlands: Elsevier. ISBN 0-444-51795-2. ISSN 0924-6509. MR 2147066. Zbl 1091.26008.
• Ehrgott, Matthias (2005). Multicriteria Optimization. Springer-Berlin. ISBN 3-540-21398-8.
• Steele, J. Michael (2004). The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities. Cambridge University Press. ISBN 978-0-521-54677-5.

 وصلات خارجية

• Hazewinkel, Michiel, ed. (2001), "Inequality", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• Graph of Inequalities by Ed Pegg, Jr.
• AoPS Wiki entry about Inequalities