معادلة شرودنگر
| جزء من سلسلة مقالات عن |
| ميكانيكا الكم |
|---|

معادلة شرودنگر ظهرت عام 1925 على يد الفيزيائي النمساوي إرڤين شرودنگر لتصف الجمل الكمومية المعتمدة على الزمن. و تحتل هذه المعادلة أهمية خاصة في ميكانيك الكم حيث تعتبر بمثابة قانون التحريك الثاني لنيوتن الذي يعتبر أساسيا في الفيزياء الكلاسيكية.
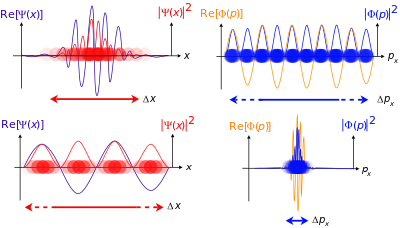
حسب التعبير الرياضي لميكانيك الكم، تترافق كل جملة فيزيائية مع فضاء هلبرت المركب (المعقد Complex) (وهو عبارة عن فضاء شعاعي) حيث توصف كل حالة لحظية للجملة بشعاع وحدة في هذا الفضاء الشعاعي، و بالتالي يكون شعاع الحالة بمثابة ترميز (تشفير encoding) لاحتمالات النتائج الممكنة من عمليات القياس بكافة أشكالها على هذه الجملة. عندما تتغير هذه الجملة مع الزمن, يصبح شعاع الحالة هذا بمثابة تابع للزمن (دالة زمنية).
أعداد الكم الناتجة عن حل معادلة شرودنگر :
- عدد الكم الرئيس n
- عدد الكم الفرعي l
- عدد الكم المغناطيسي ml
- عدد الكم المغزلي ms
أعداد الكم الناتجة.
وقد أوضح فيما بعد شرودنجر مفهوم الأوربيتال واستخدمه محل المدار بمفهوم بور
- المدار: خط وهمى دائري حول النواة تدور فيه الإلكترونات على بعد ثابت ومحدد عن النواة.
- الأوربيتال: تواجد الإلكترونات حول أي منطقة حول النواة وي جميع الإتجاهات.
Equation
Time-dependent equation
The form of the Schrödinger equation depends on the physical situation (see below for special cases). The most general form is the time-dependent Schrödinger equation (TDSE), which gives a description of a system evolving with time:[1]
where is the energy operator , is the imaginary unit, is the reduced Planck constant having the dimension of action,[2][3][note 1] (the Greek letter psi) is the state vector of the quantum system, is time, and is the Hamiltonian operator.
The position-space wave function of the quantum system is nothing but the components in the expansion of the state vector in terms of the position eigenvector . It is a scalar function, expressed as . Similarly, the momentum-space wave function can be defined as , where is the momentum eigenvector.
The most famous example is the nonrelativistic Schrödinger equation for the wave function in position space of a single particle subject to a potential , such as that due to an electric field.[4][note 2]
where (being the momentum operator), is the particle's mass, and is the Laplacian.
This is a diffusion equation, with an imaginary constant present in the transient term.
The term "Schrödinger equation" can refer to both the general equation, or the specific nonrelativistic version. The general equation is indeed quite general, used throughout quantum mechanics, for everything from the Dirac equation to quantum field theory, by plugging in diverse expressions for the Hamiltonian. The specific nonrelativistic version is a strictly classical approximation to reality and yields accurate results in many situations, but only to a certain extent (see relativistic quantum mechanics and relativistic quantum field theory).
To apply the Schrödinger equation, write down the Hamiltonian for the system, accounting for the kinetic and potential energies of the particles constituting the system, then insert it into the Schrödinger equation. The resulting partial differential equation is solved for the wave function, which contains information about the system.
Time-independent equation
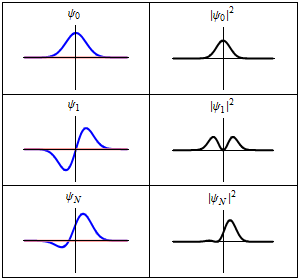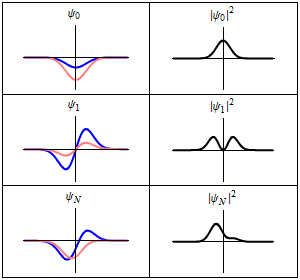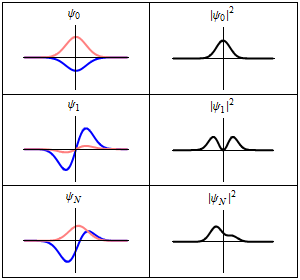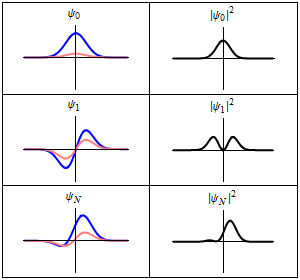
The time-dependent Schrödinger equation described above predicts that wave functions can form standing waves, called stationary states.[note 3] These states are particularly important as their individual study later simplifies the task of solving the time-dependent Schrödinger equation for any state. Stationary states can also be described by a simpler form of the Schrödinger equation, the time-independent Schrödinger equation (TISE).
where is a constant equal to the energy level of the system. This is only used when the Hamiltonian itself is not dependent on time explicitly. However, even in this case the total wave function still has a time dependency.
In the language of linear algebra, this equation is an eigenvalue equation. Therefore, the wave function is an eigenfunction of the Hamiltonian operator with corresponding eigenvalue(s) .
As before, the most common manifestation is the nonrelativistic Schrödinger equation for a single particle moving in an electric field (but not a magnetic field):
with definitions as above. Here, the form of the Hamiltonian operator comes from classical mechanics, where the Hamiltonian function is the sum of the kinetic and potential energies. That is, for a single particle in the non-relativistic limit.
The time-independent Schrödinger equation is discussed further below.
الاشتقاق
One may derive the Schrödinger equation starting from the Dirac-von Neumann axioms. Suppose the wave function represents a unit vector defined on a complex Hilbert space at some initial time . The unitarity principle requires that there must exist a linear operator, , such that for any time ,
-
(1)
Given that must remain a unit vector, the operator must therefore be a unitary transformation. As such, there exists an exponential map such that where is a Hermitian operator. This is given by the fact that the Lie algebra of the unitary group is generated by skew-Hermitian operators. If is Hermitian, then is skew-Hermitian. The first-order Taylor expansion of centered at takes the form
Substituting the above expansion into (1) then rearranging,
In the limit , this equation has the same form as the Schrödinger equation,
where the ordinary definition for the derivative was used. The operator used here denotes an arbitrary Hermitian operator. Using the correspondence principle it is possible to show that in the classical limit, using appropriate units, the expectation value of corresponds to the Hamiltonian of the system.[5]
Implications
Energy
The Hamiltonian is constructed in the same manner as in classical mechanics. However, in classical mechanics, the Hamiltonian is a scalar-valued function, whereas in quantum mechanics, it is an operator on a space of functions. It is not surprising that the eigenvalues of are the energy levels of the system.
Quantization
The Schrödinger equation predicts that if certain properties of a system are measured, the result may be quantized, meaning that only specific discrete values can occur. One example is energy quantization: the energy of an electron in an atom is always one of the quantized energy levels, a fact discovered via atomic spectroscopy. (Energy quantization is discussed below.) Another example is quantization of angular momentum. This was an assumption in the earlier Bohr model of the atom, but it is a prediction of the Schrödinger equation.
Another result of the Schrödinger equation is that not every measurement gives a quantized result in quantum mechanics. For example, position, momentum, time, and (in some situations) energy can have any value across a continuous range.[6]
Quantum tunneling

In classical physics, when a ball is rolled slowly up a large hill, it will come to a stop and roll back, because it doesn't have enough energy to get over the top of the hill to the other side. However, the Schrödinger equation predicts that there is a small probability that the ball will get to the other side of the hill, even if it has too little energy to reach the top. This is called quantum tunneling. It is related to the distribution of energy: although the ball's assumed position seems to be on one side of the hill, there is a chance of finding it on the other side.
Particles as waves
وقد كانت المعادلة الموجية لشرودنجر ومبدأ عدم التأكد لهايزنبرج والطبيعة المزدوجة للألكترون لـ"دي براولي" بمثابة المعاول التي هدمت نظرية بور "الذي نجح في التوفيق بين نظرية ماكسويل ونموذج رذرفورد" والتي اعتمدت على مفهوم المدار وأن الالكترون لا يشع في الحالة المستقرة.
Historical background and development
Following Max Planck's quantization of light (see black-body radiation), Albert Einstein interpreted Planck's quanta to be photons, particles of light, and proposed that the energy of a photon is proportional to its frequency, one of the first signs of wave–particle duality. Since energy and momentum are related in the same way as frequency and wave number in special relativity, it followed that the momentum of a photon is inversely proportional to its wavelength , or proportional to its wave number :
where is Planck's constant and is the reduced Planck constant of action[3] (or the Dirac constant). Louis de Broglie hypothesized that this is true for all particles, even particles which have mass such as electrons. He showed that, assuming that the matter waves propagate along with their particle counterparts, electrons form standing waves, meaning that only certain discrete rotational frequencies about the nucleus of an atom are allowed.[7] These quantized orbits correspond to discrete energy levels, and de Broglie reproduced the Bohr model formula for the energy levels. The Bohr model was based on the assumed quantization of angular momentum according to:
According to de Broglie the electron is described by a wave and a whole number of wavelengths must fit along the circumference of the electron's orbit:
This approach essentially confined the electron wave in one dimension, along a circular orbit of radius .
In 1921, prior to de Broglie, Arthur C. Lunn at the University of Chicago had used the same argument based on the completion of the relativistic energy–momentum 4-vector to derive what we now call the de Broglie relation.[8][9] Unlike de Broglie, Lunn went on to formulate the differential equation now known as the Schrödinger equation, and solve for its energy eigenvalues for the hydrogen atom. Unfortunately the paper was rejected by the Physical Review, as recounted by Kamen.[10]
Following up on de Broglie's ideas, physicist Peter Debye made an offhand comment that if particles behaved as waves, they should satisfy some sort of wave equation. Inspired by Debye's remark, Schrödinger decided to find a proper 3-dimensional wave equation for the electron. He was guided by William R. Hamilton's analogy between mechanics and optics, encoded in the observation that the zero-wavelength limit of optics resembles a mechanical system—the trajectories of light rays become sharp tracks that obey Fermat's principle, an analog of the principle of least action.[11] A modern version of his reasoning is reproduced below. The equation he found is:[12]
However, by that time, Arnold Sommerfeld had refined the Bohr model with relativistic corrections.[13][14] Schrödinger used the relativistic energy momentum relation to find what is now known as the Klein–Gordon equation in a Coulomb potential (in natural units):
He found the standing waves of this relativistic equation, but the relativistic corrections disagreed with Sommerfeld's formula. Discouraged, he put away his calculations and secluded himself in an isolated mountain cabin in December 1925.[15][المصدر لا يؤكد ذلك]
While at the cabin, Schrödinger decided that his earlier nonrelativistic calculations were novel enough to publish, and decided to leave off the problem of relativistic corrections for the future. Despite the difficulties in solving the differential equation for hydrogen (he had sought help from his friend the mathematician Hermann Weyl[16]) Schrödinger showed that his nonrelativistic version of the wave equation produced the correct spectral energies of hydrogen in a paper published in 1926.[16][17] In the equation, Schrödinger computed the hydrogen spectral series by treating a hydrogen atom's electron as a wave , moving in a potential well , created by the proton. This computation accurately reproduced the energy levels of the Bohr model. In a paper, Schrödinger himself explained this equation as follows:
The already ... mentioned psi-function.... is now the means for predicting probability of measurement results. In it is embodied the momentarily attained sum of theoretically based future expectation, somewhat as laid down in a catalog.
— Erwin Schrödinger[18]
This 1926 paper was enthusiastically endorsed by Einstein, who saw the matter-waves as an intuitive depiction of nature, as opposed to Heisenberg's matrix mechanics, which he considered overly formal.[19]
The Schrödinger equation details the behavior of but says nothing of its nature. Schrödinger tried to interpret it as a charge density in his fourth paper, but he was unsuccessful.[20] In 1926, just a few days after Schrödinger's fourth and final paper was published, Max Born successfully interpreted as the probability amplitude, whose modulus squared is equal to probability density.[20] Schrödinger, though, always opposed a statistical or probabilistic approach, with its associated discontinuities—much like Einstein, who believed that quantum mechanics was a statistical approximation to an underlying deterministic theory—and never reconciled with the Copenhagen interpretation.[21]
Louis de Broglie in his later years proposed a real valued wave function connected to the complex wave function by a proportionality constant and developed the De Broglie–Bohm theory.
The wave equation for particles
The Schrödinger equation is a variation on the diffusion equation where the diffusion constant is imaginary. A spike of heat will decay in amplitude and spread out; however, because the imaginary i is the generator of rotations in the complex plane, a spike in the amplitude of a matter wave will also rotate in the complex plane over time. The solutions are therefore functions which describe wave-like motions. Wave equations in physics can normally be derived from other physical laws – the wave equation for mechanical vibrations on strings and in matter can be derived from Newton's laws, where the wave function represents the displacement of matter, and electromagnetic waves from Maxwell's equations, where the wave functions are electric and magnetic fields. The basis for Schrödinger's equation, on the other hand, is the energy of the system and a separate postulate of quantum mechanics: the wave function is a description of the system.[22] The Schrödinger equation is therefore a new concept in itself; as Feynman put it:
Where did we get that (equation) from? Nowhere. It is not possible to derive it from anything you know. It came out of the mind of Schrödinger.
— Richard Feynman[23]
Consistency with the de Broglie relations

Einstein's light quanta hypothesis (1905) states that the energy E of a quantum of light or photon is proportional to its frequency (or angular frequency, )
Likewise De Broglie's hypothesis (1924) states that any particle can be associated with a wave, and that the momentum of the particle is inversely proportional to the wavelength of such a wave (or proportional to the wavenumber, ), in one dimension, by:
while in three dimensions, wavelength λ is related to the magnitude of the wavevector k:
The Planck–Einstein and de Broglie relations illuminate the deep connections between energy with time, and space with momentum, and express wave–particle duality. In practice, natural units comprising are used, as the De Broglie equations reduce to identities: allowing momentum, wave number, energy and frequency to be used interchangeably, to prevent duplication of quantities, and reduce the number of dimensions of related quantities. For familiarity SI units are still used in this article.
Schrödinger's insight,[بحاجة لمصدر] late in 1925, was to express the phase of a plane wave as a complex phase factor using these relations:
and to realize that the first order partial derivatives with respect to space were
Taking partial derivatives with respect to time gives
Another postulate of quantum mechanics is that all observables are represented by linear Hermitian operators which act on the wave function, and the eigenvalues of the operator are the values the observable takes. The previous derivatives are consistent with the energy operator (or Hamiltonian operator), corresponding to the time derivative,
where E are the energy eigenvalues, and the momentum operator, corresponding to the spatial derivatives (the gradient ),
where p is a vector of the momentum eigenvalues. In the above, the "hats" ( ˆ ) indicate these observables are operators, not simply ordinary numbers or vectors. The energy and momentum operators are differential operators, while the potential energy operator is just a multiplicative factor.
Substituting the energy and momentum operators into the classical energy conservation equation obtains the operator:
so in terms of derivatives with respect to time and space, acting this operator on the wave function Ψ immediately led Schrödinger to his equation:[بحاجة لمصدر]
Wave–particle duality can be assessed from these equations as follows. The kinetic energy T is related to the square of momentum p. As the particle's momentum increases, the kinetic energy increases more rapidly, but since the wave number |k| increases the wavelength λ decreases. In terms of ordinary scalar and vector quantities (not operators):
The kinetic energy is also proportional to the second spatial derivatives, so it is also proportional to the magnitude of the curvature of the wave, in terms of operators:
As the curvature increases, the amplitude of the wave alternates between positive and negative more rapidly, and also shortens the wavelength. So the inverse relation between momentum and wavelength is consistent with the energy the particle has, and so the energy of the particle has a connection to a wave, all in the same mathematical formulation.[24]
حركة الموجات والجسيمات
انظر أيضاً
- ثابت پلانك
- Eckhaus equation
- Fractional Schrödinger equation
- List of quantum-mechanical systems with analytical solutions
- Logarithmic Schrödinger equation
- Nonlinear Schrödinger equation
- Quantum carpet
- Quantum revival
- Relation between Schrödinger's equation and the path integral formulation of quantum mechanics
- Schrödinger field
- Schrödinger picture
- Schrödinger's cat
- Theoretical and experimental justification for the Schrödinger equation
ملاحظات
- ^ The dimension of action is that of energy multiplied by time rather than energy per time, which is the dimension of power. The SI unit of action is the joule-second whereas the SI unit of power is joule per second (watts).
- ^ For a charged particle moving under the influence of a magnetic field, see the Pauli equation.
- ^ In chemistry, stationary states are atomic and molecular orbitals.
الهامش
- ^ Shankar, R. (1943). Principles of Quantum Mechanics (2nd ed.). Kluwer Academic/Plenum Publishers. ISBN 978-0-306-44790-7.
- ^ P. R. Bunker; I. M. Mills; Per Jensen (2019). "The Planck constant and its units". J Quant Spectrosc Radiat Transfer. 237: 106594. doi:10.1016/j.jqsrt.2019.106594.
- ^ أ ب P. R. Bunker; Per Jensen (2020). "The Planck constant of action A". J Quant Spectrosc Radiat Transfer. 243: 106835. doi:10.1016/j.jqsrt.2020.106835.
- ^ "Schrodinger equation". Hyperphysics. Department of Physics and Astronomy, George State University.
- ^ Sakurai, J. J. (1995). Modern Quantum Mechanics. Reading, Massachusetts: Addison-Wesley. p. 68.
- ^ Nouredine Zettili (17 February 2009). Quantum Mechanics: Concepts and Applications. John Wiley & Sons. ISBN 978-0-470-02678-6.
- ^ de Broglie, L. (1925). "Recherches sur la théorie des quanta" [On the Theory of Quanta] (PDF). Annales de Physique. 10 (3): 22–128. Bibcode:1925AnPh...10...22D. doi:10.1051/anphys/192510030022. Archived from the original (PDF) on 9 مايو 2009. .
- ^ Weissman, M.B.; V. V. Iliev; I. Gutman (2008). "A pioneer remembered: biographical notes about Arthur Constant Lunn". Communications in Mathematical and in Computer Chemistry. 59 (3): 687–708.
- ^ Samuel I. Weissman; Michael Weissman (1997). "Alan Sokal's Hoax and A. Lunn's Theory of Quantum Mechanics". Physics Today. 50, 6: 15. doi:10.1063/1.881789.
- ^ Kamen, Martin D. (1985). Radiant Science, Dark Politics. Berkeley and Los Angeles, California: University of California Press. pp. 29–32. ISBN 978-0-520-04929-1.
- ^ Schrödinger, E. (1984). Collected papers. Friedrich Vieweg und Sohn. ISBN 978-3-7001-0573-2. See introduction to first 1926 paper.
- ^ Encyclopaedia of Physics (2nd Edition), R. G. Lerner, G. L. Trigg, VHC publishers, 1991, (Verlagsgesellschaft) 3-527-26954-1, (VHC Inc.) ISBN 0-89573-752-3
- ^ Sommerfeld, A. (1919). Atombau und Spektrallinien. Braunschweig: Friedrich Vieweg und Sohn. ISBN 978-3-87144-484-5.
- ^ For an English source, see Haar, T. (1967). "The Old Quantum Theory".
{{cite journal}}: Cite journal requires|journal=(help) - ^ Rhodes, R. (1986). Making of the Atomic Bomb. Touchstone. ISBN 978-0-671-44133-3.
- ^ أ ب Erwin Schrödinger (1982). Collected Papers on Wave Mechanics: Third Edition. American Mathematical Soc. ISBN 978-0-8218-3524-1.
- ^ Schrödinger, E. (1926). "Quantisierung als Eigenwertproblem; von Erwin Schrödinger". Annalen der Physik. 384 (4): 361–377. Bibcode:1926AnP...384..361S. doi:10.1002/andp.19263840404.
- ^ Erwin Schrödinger, "The Present situation in Quantum Mechanics", p. 9 of 22. The English version was translated by John D. Trimmer. The translation first appeared first in Proceedings of the American Philosophical Society, 124, 323–38. It later appeared as Section I.11 of Part I of Quantum Theory and Measurement by J. A. Wheeler and W. H. Zurek, eds., Princeton University Press, New Jersey 1983.
- ^
Einstein, A.; et al. "Letters on Wave Mechanics: Schrodinger–Planck–Einstein–Lorentz".
{{cite journal}}: Cite journal requires|journal=(help) - ^ أ ب ت Moore, W.J. (1992). Schrödinger: Life and Thought. Cambridge University Press. ISBN 978-0-521-43767-7.
- ^ It is clear that even in his last year of life, as shown in a letter to Max Born, that Schrödinger never accepted the Copenhagen interpretation.[20]
- ^ Molecular Quantum Mechanics Parts I and II: An Introduction to Quantum Chemistry (Volume 1), P. W. Atkins, Oxford University Press, 1977, ISBN 0-19-855129-0
- ^ The New Quantum Universe, T. Hey, P. Walters, Cambridge University Press, 2009, ISBN 978-0-521-56457-1
- ^ أ ب خطأ استشهاد: وسم
<ref>غير صحيح؛ لا نص تم توفيره للمراجع المسماةQuanta 1974
وصلات خارجية
- Hazewinkel, Michiel, ed. (2001), "Schrödinger equation", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104
- Quantum Physics – textbook by Benjamin Crowell with a treatment of the time-independent Schrödinger equation
- Linear Schrödinger Equation at EqWorld: The World of Mathematical Equations.
- Nonlinear Schrödinger Equation at EqWorld: The World of Mathematical Equations.
- The Schrödinger Equation in One Dimension as well as the directory of the book.
- All about 3D Schrödinger Equation
- Mathematical aspects of Schrödinger equations are discussed on the Dispersive PDE Wiki.
- Web-Schrödinger: Interactive solution of the 2D time-dependent and stationary Schrödinger equation
- An alternate reasoning behind the Schrödinger Equation
- Online software-Periodic Potential Lab Solves the time-independent Schrödinger equation for arbitrary periodic potentials.
- What Do You Do With a Wavefunction?
- The Young Double-Slit Experiment
- Schrodinger solver in 1, 2 and 3d
- Short description is different from Wikidata
- Articles with hatnote templates targeting a nonexistent page
- مقالات ذات عبارات بحاجة لمصادر
- Articles with unsourced statements from January 2014
- Schrödinger equation
- Differential equations
- معادلات تفاضلية جزئية
- ميكانيكا موجية
- Functions of space and time
- نظرية الكم
















![{\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=\left[{\frac {-\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} ,t)\right]\Psi (\mathbf {r} ,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4894f9a205c471cb012351a1fccdd01285b6f11c)







![{\displaystyle \left[{\frac {-\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} )\right]\Psi (\mathbf {r} )=E\Psi (\mathbf {r} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f57865f4e7f8414e2c7b1a2ae06a30eb3b0d013)