مرشح كالمان

مصفاة أو مرشح أو فلتر كلمان Kalman Filter هو مرشح يستعمل عادة لحساب أو التنبؤ بحالات نظام ديناميكي ما اعتمادا على نموذج له وعلى قياسات مشوشة. أي أنه عبارة على ملاحظ. سمي هذا المرشح باسم مخترعه الرياضياتي رودولف كالمان. أحيانا يسمى هذا المرشح أيضا بمرشح أو فلتر فينر. يقوم فلتر كالمان بحساب قيم حالة نظام ديناميكي ما بطريقة مثلى تجعل القيمة المنتظرة لمربع الفارق بين التنبؤ والحالة الصحيحة هي الأصغر.

أدوار المتغيرات في مرشح كالمان. (صورة أكبر هنا)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 مرشح كالمان بوسي المتصل واستعماله في التحكم بإرجاع الحالة

مرشح كالمان بوسي المتصل continous kalman bucy filter هو النسخة المتصلة لفلتر كالمان.

 مرشح كالمان المتقطع

مرشح كالمان المتقطع discrete kalman filter هي النسخة المتقطعة منه ولذلك النسخة أو الخوارزمية المنتشرة والمستعملة في الحواسيب.

 نموذج النظام الديناميكي تحته

Model underlying the Kalman filter. Squares represent matrices. Ellipses represent multivariate normal distributions (with the mean and covariance matrix enclosed). Unenclosed values are vectors. In the simple case, the various matrices are constant with time, and thus the subscripts are dropped, but the Kalman filter allows any of them to change each time step.

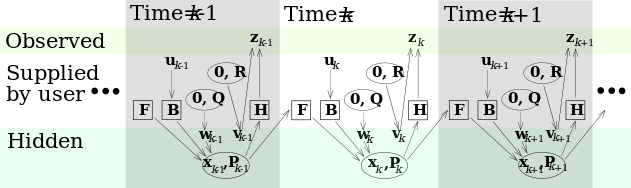
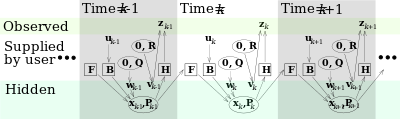
يفترض نموذج مرشح كالمان أن الحالة الحقيقية عند الزمن k قد تطورت من الحالة عند (k − 1) حسب

${\textbf {x}}_{k}={\textbf {F}}_{k}{\textbf {x}}_{k-1}+{\textbf {B}}_{k}{\textbf {u}}_{k}+{\textbf {w}}_{k}$

حيث

• F_k هي the state transition model which is applied to the previous state x_k−1;
• B_k هي the control-input model which is applied to the control vector u_k;
• w_k هي the process noise which is assumed to be drawn from a zero mean multivariate normal distribution with covariance Q_k.

${\textbf {w}}_{k}\sim N(0,{\textbf {Q}}_{k})$

At time k an observation (or measurement) z_k of the true state x_k is made according to

${\textbf {z}}_{k}={\textbf {H}}_{k}{\textbf {x}}_{k}+{\textbf {v}}_{k}$

where H_k هي the observation model which maps the true state space into the observed space and v_k is the observation noise which is assumed to be zero mean Gaussian white noise with covariance R_k.

${\textbf {v}}_{k}\sim N(0,{\textbf {R}}_{k})$

The initial state, and the noise vectors at each step {x₀, w₁, ..., w_k, v₁ ... v_k} are all assumed to be mutually independent.

 التطبيقات

• Attitude and Heading Reference Systems
• Autopilot
• Battery state of charge (SoC) estimation [1][2]
• Brain-computer interface
• Chaotic signals
• Dynamic positioning
• Economics, in particular macroeconomics, time series, and econometrics
• Inertial guidance system
• Radar tracker
• Satellite navigation systems
• Simultaneous localization and mapping
• Speech enhancement
• Weather forecasting
• Navigation Systems
• 3D-Modelling

 انظر أيضاً

• Alpha beta filter
• Covariance intersection
• Data assimilation
• Ensemble Kalman filter
• Extended Kalman filter
• Invariant extended Kalman filter
• Fast Kalman filter
• Compare with: Wiener filter, and the multimodal Particle filter estimator.
• Filtering problem (stochastic processes)
• Kernel adaptive filter
• Masreliez’s theorem
• Non-linear filter
• Predictor corrector
• Recursive least squares
• Sliding mode control - describes a sliding mode observer that has similar noise performance to the Kalman filter
• Separation principle
• Zakai equation
• Stochastic differential equations
• Volterra series

 للاستزادة

• Gelb, A. (1974). Applied Optimal Estimation. MIT Press.

• Kalman, R.E. (1960). "A new approach to linear filtering and prediction problems" (PDF). Journal of Basic Engineering. 82 (1): 35–45. Retrieved 2008-05-03.

• Kalman, R.E. (1961). "New Results in Linear Filtering and Prediction Theory". Retrieved 2008-05-03. {{cite journal}}: Cite journal requires |journal= (help); Unknown parameter |coauthors= ignored (|author= suggested) (help); Unknown parameter |verb= ignored (help)

• Harvey, A.C. (1990). Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge University Press.

• Roweis, S. (1999). "A Unifying Review of Linear Gaussian Models". Neural Computation. 11 (2): 305–345. doi:10.1162/089976699300016674. PMID 9950734. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

• Simon, D. (2006). Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches. Wiley-Interscience.

• Stengel, R.F. (1994). Optimal Control and Estimation. Dover Publications. ISBN 0-486-68200-5.

• Warwick, K. (1987). "Optimal observers for ARMA models" (PDF). International Journal of Control. 46 (5): 1493–1503. doi:10.1080/00207178708933989. Retrieved 2008-05-03.

• Bierman, G.J. (1977). Factorization Methods for Discrete Sequential Estimation. Vol. 128. Mineola, N.Y.: Dover Publications. ISBN 9780486449814. {{cite book}}: |journal= ignored (help)

• Bozic, S.M. (1994). Digital and Kalman filtering. Butterworth-Heinemann.

• Haykin, S. (2002). Adaptive Filter Theory. Prentice Hall.

• Liu, W. (2010). Kernel Adaptive Filtering: A Comprehensive Introduction. John Wiley. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

• Manolakis, D.G. (1999). Statistical and Adaptive signal processing. Artech House.

• Welch, Greg (1997). "SCAAT: Incremental Tracking with Incomplete Information" (PDF). ACM Press/Addison-Wesley Publishing Co: 333–344. doi:10.1145/258734.258876. ISBN 0-89791-896-7. {{cite journal}}: Cite journal requires |journal= (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)

• Jazwinski, Andrew H. (1970). Stochastic Processes and Filtering. Mathematics in Science and Enginerring. New York: Academic Press. p. 376.

• Maybeck, Peter S. (1979). Stochastic Models, Estimation, and Control. Mathematics in Science and Enginerring. Vol. 141–1. New York: Academic Press. p. 423. ISBN 0124807011.

• Grewal, Mohinder S.; Andrews, Angus P. (2001). Kalman filtering: theory and practice using MATLAB (PDF) (Second ed.). New York: John Wiley & Sons. p. 401. ISBN 0471392545.

• Chui, Charles K.; Chen, Guanrong (2009). Kalman Filtering with Real-Time Applications. Springer Series in Information Sciences. Vol. 17 (4th ed.). New York: Springer. p. 229. ISBN 9783540878483.

• Spivey, Ben (2010). "Constrained Nonlinear Estimation for Industrial Process Fouling". Industrial & Engineering Chemistry Research. 49 (17): 7824–7831. doi:10.1021/ie9018116. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

• Thomas Kailath, Ali H. Sayed, and Babak Hassibi, Linear Estimation, Prentice-Hall, NJ, 2000, ISBN 978-0-13-022464-4.

• Ali H. Sayed, Adaptive Filters, Wiley, NJ, 2008, ISBN 978-0-470-25388-5.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 وصلات خارجية

• A New Approach to Linear Filtering and Prediction Problems, by R. E. Kalman, 1960
• Kalman-Bucy Filter, a good derivation of the Kalman-Bucy Filter
• MIT Video Lecture on the Kalman filter
• An Introduction to the Kalman Filter, SIGGRAPH 2001 Course, Greg Welch and Gary Bishop
• Kalman filtering chapter from Stochastic Models, Estimation, and Control, vol. 1, by Peter S. Maybeck
• Kalman Filter webpage, with lots of links
• Kalman Filtering
• Kalman Filters, thorough introduction to several types, together with applications to Robot Localization
• Kalman filters used in Weather models, SIAM News, Volume 36, Number 8, October 2003.
• Critical Evaluation of Extended Kalman Filtering and Moving-Horizon Estimation, Ind. Eng. Chem. Res., 44 (8), 2451–2460, 2005.
• Source code for the propeller microprocessor: Well documented source code written for the Parallax propeller processor.
• Gerald J. Bierman's Estimation Subroutine Library: Corresponds to the code in the research monograph "Factorization Methods for Discrete Sequential Estimation" originally published by Academic Press in 1977. Republished by Dover
• Matlab Toolbox of Kalman Filtering applied to Simultaneous Localization and Mapping: Vehicle moving in 1D, 2D and 3D
• Derivation of a 6D EKF solution to Simultaneous Localization and Mapping (In PDF). See also the tutorial on implementing a Kalman Filter with the MRPT C++ libraries.
• The Kalman Filter Explained A very simple tutorial.
• The Kalman Filter in Reproducing Kernel Hilbert Spaces A comprehensive introduction.
• Matlab code to estimate Cox–Ingersoll–Ross interest rate model with Kalman Filter: Corresponds to the paper "estimating and testing exponential-affine term structure models by kalman filter" published by Review of Quantitative Finance and Accounting in 1999.
• Extended Kalman Filters explained in the context of Simulation, Estimation, Control, and Optimization