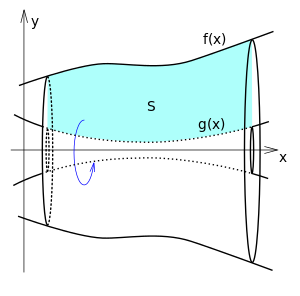
مجسم دوراني
محور الدوران (Axis of Revolution)، إذا دارت منطقة مستوية حول مستقيم في مستواها دورة كاملة (Complete Revolution)، تكون من دورانها مجسم دوراني (Solid of Revolution)، وكان الخط المستقيم الذي دارت حوله هذه المنطقة هو محور الدوران. وهو محور تماثل بالنسبة إلى المجسم الدوراني الناشيء.
حساب الحجم
رموز :
- r = نصف القطر
- h = الارتفاع
- A = المساحة أو مساحة القاعدة
- V = الحجم
يتم حساب الحجم بعدة طرق ,منها :
- تقوم الطريقة على تقسيم الجسم إلى أقراص غير متناهية.[1]
محور الدوران هو المحور السيني
- إذا كان المجسم الدوراني ينتج عن دوران منطقة مستوية حول محور السينات فإنه حجمه يعطى بالمعادلة :
-
- حيث R هي المساحة بين الدالة ومحور الدوران .
محور الدوران هو المحور الصادي
- إذا كان المجسم الدوراني ينتج عن دوران منطقة مستوية حول محور الصادات فإنه حجمه يعطى بالمعادلة :
-
- حيث R هي المساحة بين الدالة ومحور الدوران .
التكامل الطبقات الاسطوانية
التكامل بالأقراص
and about the x-axis is given by
If g(x) = 0 (e.g. revolving an area between curve and x-axis), this reduces to:
تكامل الطبقات الإسطوانية
The volume of the solid formed by rotating the area between the curves of and and the lines and about the y-axis is given by
If g(x) = 0 (e.g. revolving an area between curve and x-axis), this reduces to:
الصيغة الپارامترية
When a curve is defined by its parametric form (x(t),y(t)) in some interval [a,b], the volumes of the solids generated by revolving the curve around the x-axis or the y-axis are given by[2]
Under the same circumstances the areas of the surfaces of the solids generated by revolving the curve around the x-axis or the y-axis are given by[3]
بعض أنواع المجسمات الدورانية
- الأجسام الدورانية متنوعة بتنوع منحنيات الدوال , ولكن هناك أجسام مشهورة منها :
| اسم الجسم | ينشأ عن دوران | معادلة المنطقة المستوية | تمثيل الشكل | معادلة حساب الحجم |
|---|---|---|---|---|
| اسطوانة | مستطيل |  |
||
| مخروط | مثلث قائم الزاوية | 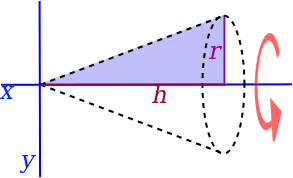 |
||
| كرة | نصف دائرة | 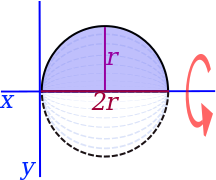 |
||
| مخروط ناقص | شبه منحرف | حيث H ارتفاع الجزء الناقص |
 |
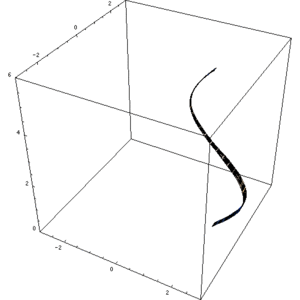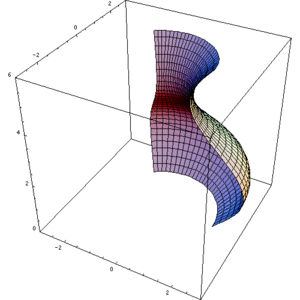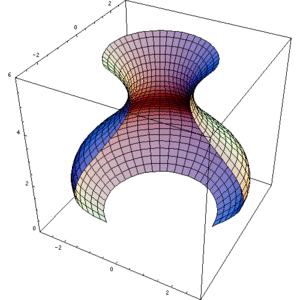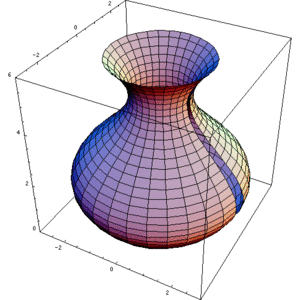
وبعض الأجسام قد تنتج من خلال المنطقة المحصورة بين داليتين ليست صفرية(انظر الشكل المقابل)
انظر أيضا
هوامش
- ^ مجسم دوراني، ويكيبيديا
- ^ Sharma, A. K. (2005). Application Of Integral Calculus. Discovery Publishing House. p. 168. ISBN 81-7141-967-4.
- ^ Singh, Ravish R. (1993). Engineering Mathematics (6th ed.). Tata McGraw-Hill. p. 6.90. ISBN 0-07-014615-2.
المصادر
- CliffsNotes.com. Volumes of Solids of Revolution. 12 Apr 2011 <http://www.cliffsnotes.com/study_guide/topicArticleId-39909,articleId-39907.html>.
- Frank Ayres, Elliott Mendelson:Schaum's outlines: Calculus. McGraw-Hill Professional 2008, ISBN 9780071508612. pp. 244-248 (online copy, p. 244, في كتب گوگل)
- Eric W. Weisstein, Solid of Revolution at MathWorld.
![{\displaystyle V=\pi \int _{a}^{b}{\left[R(x)\right]}^{2}\ \mathrm {d} x}](https://www.marefa.org/api/rest_v1/media/math/render/svg/277d758dbd0e1cd27c3aed8763e0b98abd95190e)
![{\displaystyle V=\pi \int _{a}^{b}{\left[R(y)\right]}^{2}\ \mathrm {d} y}](https://www.marefa.org/api/rest_v1/media/math/render/svg/6aadb7d4aa5c06abdaf70344c2a4853ae4ffa41b)