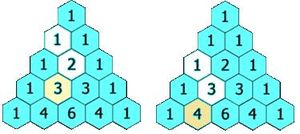
مثلث پاسكال

في مثلث پاسكال، كل عدد هو حاصل جمع العددين فوقه مباشرة.

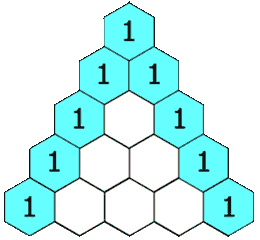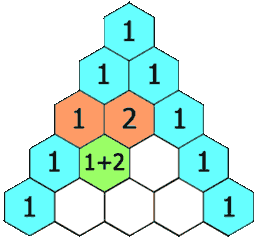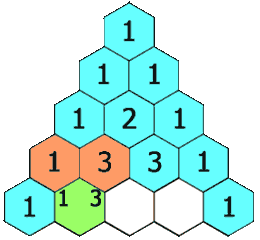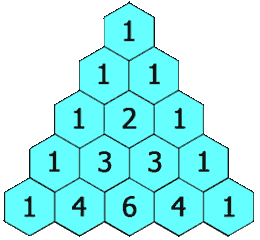
في الرياضيات مثلث باسكال هو منظومة هندسية لمكافئ ثنائي في المثلث. سميت على اسم بليز باسكال على الرغم من قيام العديد من العلماء بدراسته قبل باسكال في الهند، بلاد فارس، الصين، وإيطاليا. يتم ترقيم الصفوف في مثلث باسكال بدءًا من الصفر، وغالبًا ما تتوسط الأعداد في الصفوف ذات الأرقام الأعداد الموجودة في الصفوف الزوجية في المكان. يتم إنشاء المثلث ببساطة على النحو التالي:

1. في الصف ذو الرقم صفر، اكتب فقط الرقم 1
2. من أجل إنشاء عناصر الصف الثاني، اجمع العدد الموجود في أعلى ويمين العدد إلى العدد الموجود في أعلى ويسار العدد فينتج قيمة العنصر الجديد
3. إذا لم يوجد عنصر في أعلى ويمين (أو أعلى أو يسار العدد) اجمع صفر إلى العدد الآخر.

 مميزات مثلث باسكال:

• الأرقام التي على حافة المثلث هي كلها 1.
• الرقم الذي بجانب الحافة في السطر n (الترقيم يبدأ من 0) هو n
• مجموع الأرقام في السطر رقم n (الترقيم يبدأ من 0) هو خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^n}
• مجموع الارقام في الأماكن الزوجية في السطر مساو لمجموع الأرقام في الأماكن الفردية في نفس السطر.
• الأرقام الموجودة في كل سطر هي عبارة عن: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle 11^n } حيث n هو عبارة عن ترتيب (رقم) السطر، علماً أن السطر الأول ترتيبه (الصفر)، أي أن: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle 11^0 = 1 } .
• مجموع الأرقام بشكل مائل حتى الخط المنصف، يساوي إلى الرقم المحاذي لها بشكل مائل (الشكل ((*)) يوضح ذلك).

الشكل ((*))
في الصورة على اليمين (1+3=4)
وفي الصورة على اليسار (1+2=3)

 التاريخ

Yang Hui's triangle, as depicted by the Chinese using rod numerals, appears in a mathematical work by Zhu Shijie, dated 1303. The title reads "The Old Method Chart of the Seven Multiplying Squares" (Chinese: 古法七乘方圖; the fourth character 椉 in the image title is archaic).

Blaise Pascal's version of the triangle

 امتدادات

مثلث پاسكال يمكن مده إلى صف الأعداد السالبة.

First write the triangle in the following form:

	m = 0	m = 1	m = 2	m = 3	m = 4	m = 5	...
n = 0	1	0	0	0	0	0	...
n = 1	1	1	0	0	0	0	...
n = 2	1	2	1	0	0	0	...
n = 3	1	3	3	1	0	0	...
n = 4	1	4	6	4	1	0	...

Next, extend the column of 1s upwards:

	m = 0	m = 1	m = 2	m = 3	m = 4	m = 5	...
n = −4	1						...
n = −3	1						...
n = −2	1						...
n = −1	1						...
n = 0	1	0	0	0	0	0	...
n = 1	1	1	0	0	0	0	...
n = 2	1	2	1	0	0	0	...
n = 3	1	3	3	1	0	0	...
n = 4	1	4	6	4	1	0	...

Now the rule:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle {n \choose m} = {n-1 \choose m-1} + {n-1 \choose m}}

can be rearranged to:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle {n-1 \choose m} = {n \choose m} - {n-1 \choose m-1}}

which allows calculation of the other entries for negative rows:

	m = 0	m = 1	m = 2	m = 3	m = 4	m = 5	...
n = −4	1	−4	10	−20	35	−56	...
n = −3	1	−3	6	−10	15	−21	...
n = −2	1	−2	3	−4	5	−6	...
n = −1	1	−1	1	−1	1	−1	...
n = 0	1	0	0	0	0	0	...
n = 1	1	1	0	0	0	0	...
n = 2	1	2	1	0	0	0	...
n = 3	1	3	3	1	0	0	...
n = 4	1	4	6	4	1	0	...

This extension preserves the property that the values in the mth column viewed as a function of n are fit by an order m polynomial, namely

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle {n \choose m} = \frac{1}{m!}\prod_{k=0}^{m-1} (n-k) = \frac{1}{m!}\prod_{k=1}^{m} (n-k+1) } .

This extension also preserves the property that the values in the nth row correspond to the coefficients of (1 + x)ⁿ:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1+x)^n = \sum_{k=0}^\infty {n \choose k} x^k \quad |x| < 1 }

For example:

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1+x)^{-2} = 1-2x+3x^2-4x^3+\cdots \quad |x| < 1 }

When viewed as a series, the rows of negative n diverge. However, they are still Abel summable, which summation gives the standard values of 2ⁿ. (In fact, the n = -1 row results in Grandi's series which "sums" to 1/2, and the n = -2 row results in another well-known series which has an Abel sum of 1/4.)

Another option for extending Pascal's triangle to negative rows comes from extending the other line of 1s:

	m = −4	m = −3	m = −2	m = −1	m = 0	m = 1	m = 2	m = 3	m = 4	m = 5	...
n = −4	1	0	0	0	0	0	0	0	0	0	...
n = −3		1	0	0	0	0	0	0	0	0	...
n = −2			1	0	0	0	0	0	0	0	...
n = −1				1	0	0	0	0	0	0	...
n = 0	0	0	0	0	1	0	0	0	0	0	...
n = 1	0	0	0	0	1	1	0	0	0	0	...
n = 2	0	0	0	0	1	2	1	0	0	0	...
n = 3	0	0	0	0	1	3	3	1	0	0	...
n = 4	0	0	0	0	1	4	6	4	1	0	...

Applying the same rule as before leads to

	m = −4	m = −3	m = −2	m = −1	m = 0	m = 1	m = 2	m = 3	m = 4	m = 5	...
n = −4	1	0	0	0	0	0	0	0	0	0	...
n = −3	−3	1	0	0	0	0	0	0	0	0	...
n = −2	3	−2	1	0	0	0	0	0	0	0	...
n = −1	−1	1	−1	1	0	0	0	0	0	0	..
n = 0	0	0	0	0	1	0	0	0	0	0	...
n = 1	0	0	0	0	1	1	0	0	0	0	...
n = 2	0	0	0	0	1	2	1	0	0	0	...
n = 3	0	0	0	0	1	3	3	1	0	0	...
n = 4	0	0	0	0	1	4	6	4	1	0	...

Note that this extension also has the properties that just as

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \exp\begin{pmatrix} . & . & . & . & . \\ 1 & . & . & . & . \\ . & 2 & . & . & . \\ . & . & 3 & . & . \\ . & . & . & 4 & . \end{pmatrix} = \begin{pmatrix} 1 & . & . & . & . \\ 1 & 1 & . & . & . \\ 1 & 2 & 1 & . & . \\ 1 & 3 & 3 & 1 & . \\ 1 & 4 & 6 & 4 & 1 \end{pmatrix}, }

we have

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \exp\begin{pmatrix} . & . & . & . & . & . & . & . & . & . \\ -4 & . & . & . & . & . & . & . & . & . \\ . & -3 & . & . & . & . & . & . & . & . \\ . & . & -2 & . & . & . & . & . & . & . \\ . & . & . & -1 & . & . & . & . & . & . \\ . & . & . & . & 0 & . & . & . & . & . \\ . & . & . & . & . & 1 & . & . & . & . \\ . & . & . & . & . & . & 2 & . & . & . \\ . & . & . & . & . & . & . & 3 & . & . \\ . & . & . & . & . & . & . & . & 4 & . \end{pmatrix} = \begin{pmatrix} 1 & . & . & . & . & . & . & . & . & . \\ -4 & 1 & . & . & . & . & . & . & . & . \\ 6 & -3 & 1 & . & . & . & . & . & . & . \\ -4 & 3 & -2 & 1 & . & . & . & . & . & . \\ 1 & -1 & 1 & -1 & 1 & . & . & . & . & . \\ . & . & . & . & . & 1 & . & . & . & . \\ . & . & . & . & . & 1 & 1 & . & . & . \\ . & . & . & . & . & 1 & 2 & 1 & . & . \\ . & . & . & . & . & 1 & 3 & 3 & 1 & . \\ . & . & . & . & . & 1 & 4 & 6 & 4 & 1 \end{pmatrix} }

Also, just as summing along the lower-left to upper-right diagonals of the Pascal matrix yields the Fibonacci numbers, this second type of extension still sums to the Fibonacci numbers for negative index.

Either of these extensions can be reached if we define

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle {n \choose k} = \frac{n!}{(n-k)! k!} \equiv \frac{\Gamma(n+1)}{\Gamma(n-k+1)\Gamma(k+1)}}

and take certain limits of the gamma function, خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Gamma(z)} .

 انظر أيضاً

• Bean machine, Francis Galton's "quincunx"
• Bell triangle
• Bernoulli's triangle
• Binomial expansion
• Euler triangle
• Floyd's triangle
• Gaussian binomial coefficient
• Leibniz harmonic triangle
• Multiplicities of entries in Pascal's triangle (Singmaster's conjecture)
• Pascal matrix
• Pascal's pyramid
• Pascal's simplex
• Proton NMR, one application of Pascal's triangle
• (2,1)-Pascal triangle
• Star of David theorem
• Trinomial expansion
• Trinomial triangle

 وصلات خارجية

• Hazewinkel, Michiel, ed. (2001), "Pascal triangle", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• Eric W. Weisstein, Pascal's triangle at MathWorld.
• The Old Method Chart of the Seven Multiplying Squares (from the Ssu Yuan Yü Chien of Chu Shi-Chieh, 1303, depicting the first nine rows of Pascal's triangle)
• Pascal's Treatise on the Arithmetic Triangle (page images of Pascal's treatise, 1655; summary)
• Earliest Known Uses of Some of the Words of Mathematics (P)
• Leibniz and Pascal triangles
• Dot Patterns, Pascal's triangle, and Lucas' Theorem