طريقة مونج
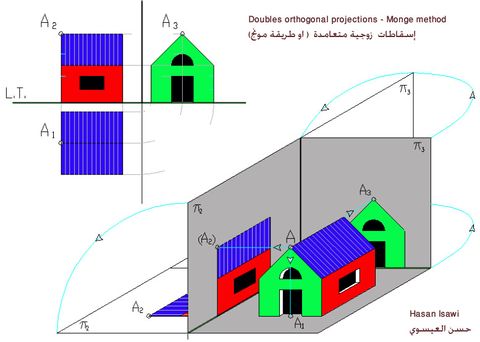
طريقة مونج في الهندسة الوصفية هي طريقة تستعمل الإسقاطات المتعامدة لتمثيل جسم ثلاثي الأبعاد. وتستمد اسمها من عالم الرياضيات الفرنسي غاسبار مونج الذي يصفها في كتابه Géométrie descriptive 1799. طريقة مونج تعتمد على الإسقاطات المتعامدة للجسم على مستويين متعامدين على بعضهما البعض، عادة واحد من هذة المستويات هو أفقي والآخر رأسي. تقاطعهم يسمى خط الأرض. بعد أن تتم عمليات الإسقاط يُقلب المستوى الرأسي حول خط ألأرض, وبعكس عقارب الساعة, لجعله يتطابق مع المستوي الأفقي. هدف هذة العملية هو تيسير عمليات الرسم التي تسمح بوضع الإسقاطات المتعامدة (خريطة، واجهة) لأي شكل هندسي في حالة تقابل.
تمثيل الكيانات الهندسية الرئيسية
تمثيل نقطة
في طريقة مونج نقطة A في الفراغ تُمثل عن طريق إسقاطين عموديين على مستويات الإسقاط:π2 π1. نقطة التقاطع بين الخط العمودي المار بالنقطة A والمستوى الأفقي π1, هي المسقط الأول (أو الأفقي) للنقطة A ويُرمز لها A1. بطريقة مماثلة يحدد المسقط الثاني A2 كنقطة تقاطع بين π2 (مستوى الإسقاط الثاني) والخط المار بالنقطة A.
- المستوى الأفقي π1: يسمى مستوى الإسقاط الأول
- المستوى الراسي π2: يسمى مستوى الإسقاط الثاني
- ألاتجاه العمودي على π1 يسمى مركز الإسقاط الأول
- ألاتجاه العمودي على π2 يسمى مركز الإسقاط الثاني
- الخط العمودي على π1, يسمى خط الإسقاط الأول
- الخط العمودي على π2, يسمى خط الإسقاط الثاني
- ارتفاع A: مسافة (أو بُعد) النقطة A عن π1
- بروز A: مسافة النقطة A عن π2
مثال
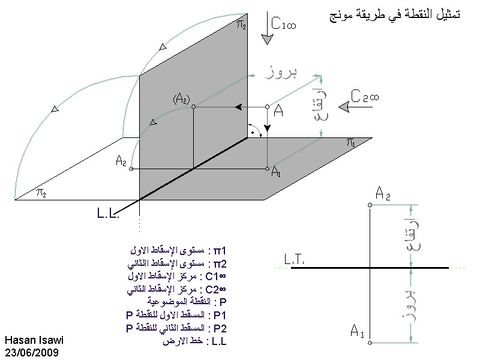
لنعين نقطة P في الزاوية الزوجية الأولى (I diedro), الإسقاط المونجي للنقطة P يكمن في الخطوات التالية:
- الإسقاط الأول P1 للنقطة P, يحدد كنقطه تقاطع بين الخط الرأسي المار بالنقطة P والمستوى الأول π1 (يسمى أيضاً مستوى الاسقاط الافقي).
- الإسقاط الثاني P2 للنقطة P, يحدد كنقطه تقاطع بين مستوى الإسقاط الثاني π2 (يسمى أيضاً مستوى الاسقاط الامامي) والخط العمودي على π2 (يسمى خط الإسقاطي الثاني).
المستوى المار بالنقطة P والعمودي على المستويين π1 وπ2, يقطعهما بخطين عموديين على خط الأرض. نقطة تقاطع هذا المستوى مع خط الأرض تسمى نقطة مرجع P ويرمز لها P0 (بي زيرو). وبهذا:
- ارتفاع P = المسقيم P_P1 الذي يساوي أيضاً P2_P0
- بروز P = المسقيم P_P2 الذي يساوي أيضاً P1_P0
تمثيل خط
الإسقاطات المتعامدة r1 r2 لخط r موضوع في الفراغ, تُحدد نظرياً هكذا:
- r1 كخط تقاطع بين π1 والمستوى الراسي المار بالخط r.
- وبالمثل r2، يحدد كخط تقاطع بين π2 والمستوى العمودي على π2 والمار بالخط r.
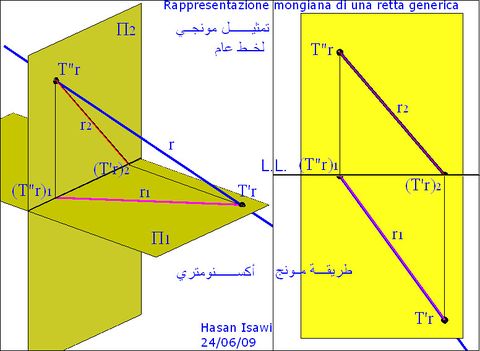
عملياً، لتحديد الإسقاطات المونجية (r1 r2)، لخط r ,على سبيل المثال r1، من الضروري تحديد إسقاطين (P1 Q1) لنقطتين (P Q) ينتميان للخط r. ولأن الخط r هو كيان غير محدودة طولياً، فتلك النقطتين يمكن ان يكونان آثار ذلك الخط r، أي نقاط التقاطع (T'r T"r) بين r ومستويات الإسقاط (π2 π1) (وربما T"'r مع مستوى الاسقاط الثالث π3).
- نقطة التقاطع T'r بين خط r ومستوى الاسقاط الأول π1، يسمى الاثر الأول للخط r.
- نقطة التقاطع T"r بين خط r وπ2، يسمى الاثر الثاني للخط r.
تمثيل مستوى
تاريخ
مونج تعهد بعدم الكشف عن الطريقة الموصوفة أعلاه، التي كانت سر عسكري لمده 15 عاما. فقط في 1794، سمح للتدريسها في باريس. [1]
ببليوغرافيا
- الهندسة الوصفية من تأليف البروفسور حسن العيسوي وتيتسيانا بريمافيرا - تاريخ النشر : 13 يونيو 07 - (كتاب باللغة الايطالية)
- "النظر بواسطة العقل" (Vedere con la mente) فهم الفراغ الهندسي بدون إدراكة بصريا- Nasini Lamberto - Isawi Hasan- 2006
- Geometria descrittiva CD-ROM - Hasan Isawi - 1999 (الهندسة الوصفية في سي دي روم - باللغة الايطالية)