النسبة الذهبية

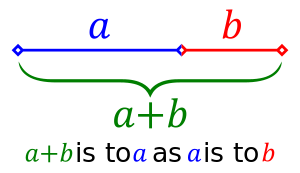
في الرياضيات والفنون، يكون رقمان في النســــبة الذهبية golden ratio (φ) إذا كانت نسبة مجموع الكميتين إلى الكمية الأكبر هي تساوي نسبة الكمية الأكبر إلى الكمية الأصغر. الرسم إلى يسار يوضح العلاقة الهندسية. ويُعبـَّر عنها جبرياً كالتالي:

أقسام من خط في نسبة ذهبية

مستطيل ذهبي حيث الضلع الأطول a والضلع الأقصر b، حين يوضع بالقرب من مربع طول ضلعه a، فإنه ينتج مثلث ذهبي مماثل طول ضلعه الأكبر a + b وطول ضلعه الأقصر a. وهو ما يوضح العلاقة

{\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi

.

{\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi ,

حيث يمثل الحرف اليوناني فاي ( $\varphi$ ) النسبة الذهبية. وقيمتها هي:

\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\ldots .

^[1]

كان الإغريق أول من وضع النظريات العملية الدقيقة للفنون كالرسم والنحت والموسيقى ، فقد قاموا بربطها بالرياضيات وبذلك طوروا علوماَ مثل علم هندسة الأشكال الذي يجمع بين الرياضيات والرسم- ومنذ2400 عام وخلال إشتغال الإغريق في العلوم و الفنون إكتشف عالم الرياضيات إقليدس النسبة الذهبية وجاءت منه أول إشارة لذلك . إن مايميز الحضارة الإغريقية إنها إمتلكت فكراَ رقيقاَ ناعماَ إعتنى بالطبيعة والفلسفة ، فكانت فنونها مثل هذا الفكر رقيقة جميلة .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

الحساب

قائمة الأعداد الأعداد الغير النسبية والأعداد الغير النسبية المتوقعة γ ζ(3) √2 √3 √5 φ ρ δ_S $e$ $π$ δ
ثنائي	1.1001111000110111011…
عشري	1.6180339887498948482…
ستة عشري	1.9E3779B97F4A7C15F39…
Continued fraction	$1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}}$
Algebraic form	${\frac {1+{\sqrt {5}}}{2}}$
متسلسلة لانهائية	${\frac {13}{8}}+\sum _{n=0}^{\infty }{\frac {(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}}$

Two quantities a and b are said to be in the golden ratio φ if:

{\frac {a+b}{a}}={\frac {a}{b}}=\varphi .

One method for finding the value of φ is to start with the left fraction. Through simplifying the fraction and substituting in b/a = 1/φ,

{\frac {a+b}{a}}=1+{\frac {b}{a}}=1+{\frac {1}{\varphi }},

it is shown that

1+{\frac {1}{\varphi }}=\varphi .

Multiplying by φ gives

\varphi +1=\varphi ^{2}

which can be rearranged to

{\varphi }^{2}-\varphi -1=0.

Using the quadratic formula gives the only positive solution as

\varphi ={\frac {1+{\sqrt {5}}}{2}}=1.61803\,39887\dots .

التاريخ

اقترح عالم الرياضيات مارك بار استخدام أول حرف في اسم النحات اليوناني فيدياس، فاي، ليرمز إلى النسبة الذهبية. وعادة، يُستخدم الشكل الأصغر (φ). وأحياناً، فإن الشكل الأكبر (Φ) يُستخدم كمقلوب النسبة الذهبية، 1/φ.^[2]

The golden ratio has fascinated Western intellectuals of diverse interests for at least 2,400 years. According to Mario Livio:

Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. But the fascination with the Golden Ratio is not confined just to mathematicians. Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.^[3]

Ancient Greek mathematicians first studied what we now call the golden ratio because of its frequent appearance in geometry. The division of a line into "extreme and mean ratio" (the golden section) is important in the geometry of regular pentagrams and pentagons. The Greeks usually attributed discovery of this concept to Pythagoras or his followers. The regular pentagram, which has a regular pentagon inscribed within it, was the Pythagoreans' symbol.

Euclid's Elements (Greek: Στοιχεῖαcode: grc is deprecated ) provides the first known written definition of what is now called the golden ratio: "A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less."^[4] Euclid explains a construction for cutting (sectioning) a line "in extreme and mean ratio", i.e. the golden ratio.^[5] Throughout the Elements, several propositions (theorems in modern terminology) and their proofs employ the golden ratio.^[6] Some of these propositions show that the golden ratio is an irrational number.

The name "extreme and mean ratio" was the principal term used from the 3rd century BC^[4] until about the 18th century.

The modern history of the golden ratio starts with Luca Pacioli's De divina proportione of 1509, which captured the imagination^{[بحاجة لمصدر]} of artists, architects, scientists, and mystics with the properties, mathematical and otherwise, of the golden ratio.

Michael Maestlin, first to publish a decimal approximation of the golden ratio, in 1597.

The first known approximation of the (inverse) golden ratio by a decimal fraction, stated as "about 0.6180340," was written in 1597 by Michael Maestlin of the University of Tübingen in a letter to his former student Johannes Kepler.^[7]

Since the twentieth century, the golden ratio has been represented by the Greek letter Φ or φ (phi, after Phidias, a sculptor who is said to have employed it) or less commonly by τ (tau, the first letter of the ancient Greek root τομή—meaning cut).^[8]^[9]

خط زمني

Timeline according to Priya Hemenway.^[10]

Phidias (490–430 BC) made the Parthenon statues that seem to embody the golden ratio.
Plato (427–347 BC), in his Timaeus, describes five possible regular solids (the Platonic solids: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron), some of which are related to the golden ratio.^[11]
Euclid (c. 325–c. 265 BC), in his Elements, gave the first recorded definition of the golden ratio, which he called, as translated into English, "extreme and mean ratio" (Greek: ἄκρος καὶ μέσος λόγος).^[4]
Fibonacci (1170–1250) mentioned the numerical series now named after him in his Liber Abaci; the ratio of sequential elements of the Fibonacci sequence approaches the golden ratio asymptotically.
Luca Pacioli (1445–1517) defines the golden ratio as the "divine proportion" in his Divina Proportione.
Michael Maestlin (1550–1631) publishes the first known approximation of the (inverse) golden ratio as a decimal fraction.
Johannes Kepler (1571–1630) proves that the golden ratio is the limit of the ratio of consecutive Fibonacci numbers,^[12] and describes the golden ratio as a "precious jewel": "Geometry has two great treasures: one is the Theorem of Pythagoras, and the other the division of a line into extreme and mean ratio; the first we may compare to a measure of gold, the second we may name a precious jewel." These two treasures are combined in the Kepler triangle.
Charles Bonnet (1720–1793) points out that in the spiral phyllotaxis of plants going clockwise and counter-clockwise were frequently two successive Fibonacci series.
Martin Ohm (1792–1872) is believed to be the first to use the term goldener Schnitt (golden section) to describe this ratio, in 1835.^[13]
Édouard Lucas (1842–1891) gives the numerical sequence now known as the Fibonacci sequence its present name.
Mark Barr (20th century) suggests the Greek letter phi (φ), the initial letter of Greek sculptor Phidias's name, as a symbol for the golden ratio.^[14]
Roger Penrose (b.1931) discovered a symmetrical pattern that uses the golden ratio in the field of aperiodic tilings, which led to new discoveries about quasicrystals.

ومن خلال ذلك تم إكتشاف متتالية عجيبة تفضي لدارسيها الى الكثير من الحقائق و المعلومات المهمة في فهم التصميم الهندسي لهذا الكون البديع بما فيه من معلومات . كما إنها ألهمت المهندسين و الفنانين والرياضيين والخطاطين وغيرهم إلى إكتشاف أسرار الجمال الذي لانظير له على الإطلاق . وهذه المتتالية هي :-

(0.1.1.2.3.5.8.13.21.34.55.89.144.233.377.610.987.1596.2584.4186، 0764………… )

أي إنها تبدأ بالصفر والى اللانهاية . وقد ساهم في وضع هذه المتتالية علماء مشهورين وعلى رأسهم (فيبو ناتشي )فسميت هذه المثالية بمتتالية فيبوناتشي . و من هذه المتتالية وجدت نسب تظهر من خلالها ملامح الجمال لكل شيء من حولنا . ولتوضيح الفكرة نذكر للقاريء الأمور التالية :-

1- يلاحظ من المتتالية ان أي رقم فيها يساوي مجموع الرقمين اللذين يسبقانه

( شكل 1)

2-إن أجمل تقسيم لأي مستقيم أوأية مساحة أو منظر أو صورة أو أي كا ئن سواء أكان إنساناَ أحيواناَ او جماداَ إذا كانت نسبة الجزءالأكبر الى الجزء الى الجزء الأصغر = 1.618 فإن هذا التقسيم يكون أجمل ما عليه ذلك الشيء وإذا قسم المستقيم الى قسمين وكانت النسبة بين مجموع القسمين الى القسم الأكبر يساوي لنسبة بين العدد الأكبر الى العدد الأصغر = 1.618 فإن هذا المستقيم يسمى بالمستقيم الذهبي،وتكون مريحة للبصر وتمثل أهم معايير الجمال . ويرمز لهذه النسبة بالحرف اللاتيني (فاي).

3-يلاحظ من المتتالية أن حاصل قسمة أي رقم على الرقم الذي قبله يقترب شيئاَ فشيئاَ من النسبة الذهبية (فاي) .لاحظ الجدول المرفق (شكل 2).

4-وإذا ربعت هذه الأرقام وجعلت ممثلة لمساحات ثم رسمت هذه المساحات كما في الشكل أدناه(3) ،ثم قمنا برسم ربع دائرة في كل مربع بحيث يتصل طرف نهاية ربع الدائرة الأولى (الأصغر) بطرف ربع الدائرة التالية نحصل على شكل متميز كما موضح في الصورة ادناه .لاحظ الإلتواء ونسبة التباعد بين أقواسه .

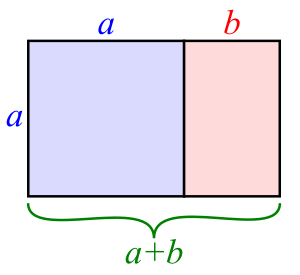
أما المستطيل الذهبي فهو الذي تكون فيه نسبة ( الضلع الكبير الى الضلع الصغير )للمستطيل الصغير نسبة (الضلع الكبير الى الضلع الصغير ) للمستطيل الكبير فاي

والمستطيل الذهبي هذا هو أحد تطبيقات متتالية فيبوناتشي إذ يظهر ذلك في اعمال المصورين والرسامين والمعماريين بغية إظهار ملامح الإ بداع والجمال في أعمالهم . وهناك المثلث الذهبي والمضلع الذهبي ، إذ يظهر في كل منهما الرقم الذهبي . فخماسي الآضلاع المنتظم هو شكل هندسي ذو خمسة أضلاع وأضلاعه وزواياه متقايسة . وفي هذا الشكل يكون خارج قسمة القطر على أحد الأضلاع يساوي (فاي).

من تطبيقات المستطيل الذهبي ،فن التصوير والرسم . فمثل هؤلاء الفنانين يحرصون على توزيع العمل الفني وفق معايير الجمال المتمثلة بالنسبة (فاي) وكل ما كانت أبعاده أقرب الى هذه النسبة كان العمل أروع . فالفنان دافنشي صمم لوحة المانوليزا وفق النسبة (فاي) فظهرت بروعتها المعروفة ،وهكذا فعل مع لوحاته الأخرى ،وسار على هذا النهج فنانون آخرون فأبدعوا.

ومن التطبيقات على الإلتواء وفق (فاي) ، مايظهر في الطبيعة مثل التواء الحلزون والقواقع ودوامات المجرات وبعض الزهور والتواء خطوط باطن الكف وخطوط إصبع الإبهام وبقية الأصابع والأصداف البحرية وإلتواء فروع الأشجار وسعف النخيل وأمواج البحر وإنحناءات خطوط اللوحات الفنية المشهورة بحيث يكون هناك إلتواء يقود العين نحو المركز سواء أكانت الصورة لجسم أو لعدة أجسام ، فهي ليست تركيبات عشوائية وإنما تخضع لتوازن رقمي مدهش .

إن هذه الأشكال اللولبية تقوم على أساس النسبةالذهبية في كل إنحناء أوإلتواء .

أما في الموسيقى فقد نجح الموسيقيون ومؤلفو السمفونيات في الحصول على جمل موسيقية رائعة

وذلك بجعل ضغطات مفاتيح الآلة (مثل البيانو) يجري على وفق تباعد رياضي ثابت وفقاَ لمتتالية فيبوناتشي . فالفرقة الموسيقية الأمريكية ألفت أغنية بعنوان ( لاتيرا ) وفيها جمل غنائية مقاطعها (3.5.8.13.3.5.8.5.3.2) . أما الثانية فهي (8.5.3.2.1.1.2) وهذه كلها أرقام فيبوتاشي وهكذا.

والنسبة هذه مريحة للعين وتشكل أهم معايير الجمال في تصميم العمارات والديكورات وتصميم أغلفة المجلات.

وفي عالم البيولوجيا والتكاثر فإن هذه النسبة تظهر في أية خلية للنحل

فنجد مثلاَ أن عدد الإناث فيها مقسوم على عدد الذكور فيها يعطي النسبة الذهبية.

وفي الأرانب إذا تركنا زوج من الأرانب (ذكر و أنثى )في حقل محدود لمدة من الزمن كافية وتحت ظروف ملائمة، نلاحظ أن عددها يتزايد على وفق أرقام فيبوناتشي .

وحتى قطع الآثاث والأدوات البسيطة وكل مايحيطنا يبدو جميلاَ إذا خضع للنسبة الذهبية سواء أكانت مستقيمات أومساحات أو أمور أخرى.

في أزمنة بعيدة بنى الفراعنة أهراماتهم على وفق هذه النسبة (فاي) فجعلوا المسافة من قمة الهرم إلى منتصف أحد أضلاع وجه الهرم مقسومة على المسافة إلى المسافة من القمة نفسها الى مركز القاعدة المربعة تساوي (فاي) .

وإن أشهر المساجد في العالم الإسلامي كجامع القيروان روعيت فيه تلك النسبة في بناءه

وأروع المناظر الطبيعية تلك التي تبدو للناظر بحيث يكون فيها توزيع اليابسة والبحر والسماء خاضع لهذه النسبة وقد يكون أجملها تلك التي يكون فيها خط الأفق يحتل اكثر من ثلثي الصورة قليلا او أن تحتل السماء اكثر من ثلثي الصورة قليلا .وينطبق الأمر نفسه على الفن التشكيلي. ويكون العمل أروع كلما كانت نسب مكوناته مقتربة من النسبة الذهبية.

من ناحية اخرى يسعى المهندسون المعماريون الى جعل اجزاء البناية التي يصممونها , متناسبة مع بعضه وفقا للنسبة (فاي) فتبدو رائعة

لنأخذ جسم الإنسان فيبدو أجمل كلما كانت النسب التالية أقرب من النسبة ا لذهبية لتقسيم المستقيم الذهبي.خذ مثلاَ

السرة تقسم جسم الإنسان الى قسمين النسبة بينهما = (فاي)

المسافة من السرة الى قمة الرأ س تقسمها الحنجرة = (فاي)

المسافة من السرة الى القدمين تقسمها الركبة = (فاي)

المسافة من الكتف الى أطراف أصابع اليد مقسومة على المسافة من الكوع الى أطراف الأصابع (فاي) *المسافة بين الحنك و الشفة السفلى مقسومة على المسافة بين الأنف والشفة العلي (فاي)

المسافة من فتحة الفم الى إرتفاع الأنف (فاي) .....وهكذا.

وكل هذا يمثل التوزيع الأمثل لأجزاء جسم الإنسان .

لذا يتم إختيار ملكات الجمال في الكون وفقا لهذه النسبة .

ويمكنناإعطاء أمثلة أخرى ينطبق فيها الرمز الجمالي موضوع بحثنا , خذ مثلاَأبعاد السيارة واجزاء جسم الحيوان وقوقعة الأذن وزهرة دوار الشمس وحراشف الصنوبر وتوزيع البذورفي بعض الزهور بشكل دائري بحيث يكون محيط أية دائرة الى الدائرة الآصغر = (فاي )وكذلك نجم البحرالذي يمتاز بشكله الخماسي الأضلاع الذهبي المتداخل ,وضربات القلب ولولبية الحمض النووي وكل ذلك أمثلة للنسبة الذهبية

إن الإقتراب من النسبة الذهبية لجميع أجزاء الأمور يكون ملفتاَ للأنظار ويبعث على الراحة النفسية ويجعلها أقرب الى التكامل الجمالي .

وحتى المحاضرون يجب عليهم الإنتباه الى توزيع وقت محاضرتهم على وفق أزمان تنسجم مع النسبة الذهبية لتعطي المحاضرة ثمارها ,فمن المستحسن أن يكون زمن المقدمة بحدود الثلث ,وسوف يضطرب المتلقي إذا كان طول باقي المحاضرة قريباَ من طول المقدمة .

وعند ملاحظة خطوط باطن كف الإنسان نجد أن كل خط يزداد تقوسه بنسبة 16.8% عن الذي قبله وأن إلتواء هذه الخطوط وكذلك إلتواء خطوط بصمة الإصبع لأي إصبع (الإبهام مثلاَ)كلها تخضع للنسبة الذهبية (فاي), وكذا الأمر بالنسبة الى عرض السن الأو ل الى عرض السن المجاور له = (فاي) .

اذن الطبيعة احترمت الجمال وعلمتنا كيف نصنعه لكل شيء من حولنا فتذكر هذه النسبة دائما لتحس بالجمال

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

طالع أيضاً

المصادر

http://panoramanews.com.au/oldsite/index.php?option=com_content&view=article&id=1554:2012-01-29-08-17-33&catid=84:2011-12-09-13-22-25&Itemid=80

^ The golden ratio can be derived by the quadratic formula, by starting with the first number as 1, then solving for 2nd number x, where the ratios (x + 1)/x = x/1 or (multiplying by x) yields: x + 1 = x², or thus a quadratic equation: x² − x − 1 = 0. Then, by the quadratic formula, for positive x = (−b + √(b² − 4ac))/(2a) with a = 1, b = −1, c = −1, the solution for x is: (−(−1) + √((−1)² − 4·1·(−1)))/(2·1) or (1 + √(5))/2.
^ خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة MathWorld GR Conjugate
^ Mario Livio,The Golden Ratio: The Story of Phi, The World's Most Astonishing Number, p.6
^ ^أ ^ب ^ت خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة Elements 6.3
^ Euclid, Elements, Book 6, Proposition 30.
^ Euclid, Elements, Book 2, Proposition 11; Book 4, Propositions 10–11; Book 13, Propositions 1–6, 8–11, 16–18.
^ "The Golden Ratio". The MacTutor History of Mathematics archive. Retrieved 2007-09-18.
^ خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة livio
^ Eric W. Weisstein, Golden Ratio at MathWorld.
^ Hemenway, Priya (2005). Divine Proportion: Phi In Art, Nature, and Science. New York: Sterling. pp. 20–21. ISBN 1-4027-3522-7.
^ Plato (360 BC) (Benjamin Jowett trans.). "Timaeus". The Internet Classics Archive. Retrieved May 30, 2006. {{cite web}}: Check date values in: |year= (help)
^ James Joseph Tattersall (2005). Elementary number theory in nine chapters (2nd ed.). Cambridge University Press. p. 28. ISBN 978-0-521-85014-8.
^ Underwood Dudley (1999). Die Macht der Zahl: Was die Numerologie uns weismachen will. Springer. p. 245. ISBN 3-7643-5978-1.
^ Cook, Theodore Andrea (1979) [1914]. The Curves of Life. New York: Dover Publications. ISBN 0-486-23701-X.

للاستزادة

Doczi, György (2005) [1981]. The Power of Limits: Proportional Harmonies in Nature, Art, and Architecture. Boston: Shambhala Publications. ISBN 1-59030-259-1.
Huntley, H. E. (1970). The Divine Proportion: A Study in Mathematical Beauty. New York: Dover Publications. ISBN 0-486-22254-3.
Livio, Mario (2002) [2002]. The Golden Ratio: The Story of PHI, the World's Most Astonishing Number (Hardback ed.). NYC: Broadway (Random House). ISBN 0-7679-0815-5.
Joseph, George G. (2000) [1991]. The Crest of the Peacock: The Non-European Roots of Mathematics (New ed.). Princeton, NJ: Princeton University Press. ISBN 0-691-00659-8.
Sahlqvist, Leif (2008). Cardinal Alignments and the Golden Section: Principles of Ancient Cosmography and Design (3rd Rev. ed.). Charleston, SC: BookSurge. ISBN 1-4196-2157-2.
Schneider, Michael S. (1994). A Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and Science. New York: HarperCollins. ISBN 0-06-016939-7.
Stakhov, A. P. (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. Singapore: World Scientific Publishing. ISBN 978-981-277-582-5.
Walser, Hans (2001) [Der Goldene Schnitt 1993]. The Golden Section. Peter Hilton trans. Washington, DC: The Mathematical Association of America. ISBN 0-88385-534-8.
Scimone, Aldo (1997). La Sezione Aurea. Storia culturale di un leitmotiv della Matematica. Palermo: Sigma Edizioni. ISBN 88.7231.025.6. {{cite book}}: Check |isbn= value: invalid character (help)

وصلات خارجية

"Golden Section" by Michael Schreiber, Wolfram Demonstrations Project, 2007.
Golden Section in Photography: Golden Ratio, Golden Triangles, Golden Spiral
Eric W. Weisstein, Golden Ratio at MathWorld.
"Researcher explains mystery of golden ratio". PhysOrg. December 21, 2009..
Knott, Ron. "The Golden section ratio: Phi". Information and activities by a mathematics professor.
The Pentagram & The Golden Ratio. Green, Thomas M. Updated June 2005. Archived November 2007. Geometry instruction with problems to solve.
قالب:Cite arxiv Proves formulas that involve the golden mean and the Euler totient and Möbius functions.

الكلمات الدالة:

[quadform-1] The golden ratio can be derived by the quadratic formula, by starting with the first number as 1, then solving for 2nd number x, where the ratios (x + 1)/x = x/1 or (multiplying by x) yields: x + 1 = x², or thus a quadratic equation: x² − x − 1 = 0. Then, by the quadratic formula, for positive x = (−b + √(b² − 4ac))/(2a) with a = 1, b = −1, c = −1, the solution for x is: (−(−1) + √((−1)² − 4·1·(−1)))/(2·1) or (1 + √(5))/2.

[MathWorld_GR_Conjugate-2] خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة MathWorld GR Conjugate

[3] Mario Livio,The Golden Ratio: The Story of Phi, The World's Most Astonishing Number, p.6

[Elements_6.3-4] أ ^ب ^ت خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة Elements 6.3

[5] Euclid, Elements, Book 6, Proposition 30.

[6] Euclid, Elements, Book 2, Proposition 11; Book 4, Propositions 10–11; Book 13, Propositions 1–6, 8–11, 16–18.

[7] "The Golden Ratio". The MacTutor History of Mathematics archive. Retrieved 2007-09-18.

[livio-8] خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة livio

[9] Eric W. Weisstein, Golden Ratio at MathWorld.

[Hemenway,P-10] Hemenway, Priya (2005). Divine Proportion: Phi In Art, Nature, and Science. New York: Sterling. pp. 20–21. ISBN 1-4027-3522-7.

[11] Plato (360 BC) (Benjamin Jowett trans.). "Timaeus". The Internet Classics Archive. Retrieved May 30, 2006. {{cite web}}: Check date values in: |year= (help)

[tatt-12] James Joseph Tattersall (2005). Elementary number theory in nine chapters (2nd ed.). Cambridge University Press. p. 28. ISBN 978-0-521-85014-8.

[13] Underwood Dudley (1999). Die Macht der Zahl: Was die Numerologie uns weismachen will. Springer. p. 245. ISBN 3-7643-5978-1.

[14] Cook, Theodore Andrea (1979) [1914]. The Curves of Life. New York: Dover Publications. ISBN 0-486-23701-X.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]