متعامد المماسات Orthoptic (geometry)

In the geometry of curves, an orthoptic is the set of points for which two tangents of a given curve meet at a right angle.

قطع مكافئ

Orthoptic of the parabola (its directrix)

قطع ناقص

Orthoptic of the ellipse (its director circle)

Minimum bounding box of the ellipse (circumscribed by the orthoptic circle)

Major and minor axes of the ellipse

Hyperbola

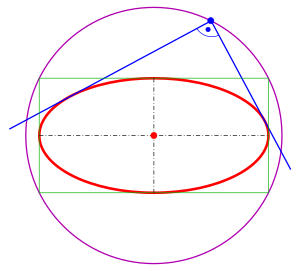
Orthoptic of the hyperbola (its director circle)

xy

-axes and hyperbolic asymptotes

أمثلة:

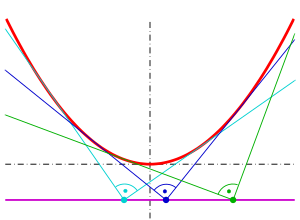
The orthoptic of a parabola is its directrix (proof: see below),
The orthoptic of an ellipse خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{x^2}{a^2} + \tfrac{y^2}{b^2} = 1} is the director circle خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2 + y^2 = a^2 + b^2} (see below),
The orthoptic of a hyperbola خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{x^2}{a^2} - \tfrac{y^2}{b^2} = 1,\ a > b} is the director circle خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2 + y^2 = a^2 - b^2} (in case of $a \leq b$ there are no orthogonal tangents, see below),
The orthoptic of an astroid خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{2/3} + y^{2/3} = 1} is a quadrifolium with the polar equation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=\tfrac{1}{\sqrt{2}}\cos(2\varphi), \ 0\le \varphi < 2\pi} (see below).

تعميمات:

An isoptic is the set of points for which two tangents of a given curve meet at a fixed angle (see below).
An isoptic of two plane curves is the set of points for which two tangents meet at a fixed angle.
Thales' theorem on a chord $PQ$ can be considered as the orthoptic of two circles which are degenerated to the two points $P$ and $Q$ .

متامد مماسات قطع مكافئ

Any parabola can be transformed by a rigid motion (angles are not changed) into a parabola with equation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = ax^2} . The slope at a point of the parabola is خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle m = 2ax} . Replacing $x$ gives the parametric representation of the parabola with the tangent slope as parameter: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\tfrac{m}{2a},\tfrac{m^2}{4a} \right) \! .} The tangent has the equation $y=mx+n$ with the still unknown $n$ , which can be determined by inserting the coordinates of the parabola point. One gets $y=mx-{\tfrac {m^{2}}{4a}}\;.$

If a tangent contains the point $(x 0, y 0)$ , off the parabola, then the equation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_0 = m x_0 -\frac{m^2}{4a} \quad \rightarrow \quad m^2 - 4ax_0\,m + 4ay_0 = 0} holds, which has two solutions $m 1$ and $m 2$ corresponding to the two tangents passing $(x 0, y 0)$ . The free term of a reduced quadratic equation is always the product of its solutions. Hence, if the tangents meet at $(x 0, y 0)$ orthogonally, the following equations hold: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1 m_2 = -1 = 4 a y_0} The last equation is equivalent to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_0 = -\frac{1}{4a}\, , } which is the equation of the directrix.

متعامد مماسات قطع ناقص وقطع زائد

قطع ناقص

Let خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle E:\; \tfrac{x^2}{a^2} + \tfrac{y^2}{b^2} = 1 } be the ellipse of consideration.

The tangents to the ellipse خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} at the vertices and co-vertices intersect at the 4 points خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\pm a, \pm b)} , which lie on the desired orthoptic curve (the circle خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2+y^2 = a^2 + b^2} ).
The tangent at a point خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u,v)} of the ellipse خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} has the equation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tfrac{u}{a^2} x + \tfrac{v}{b^2} y = 1} (see tangent to an ellipse). If the point is not a vertex this equation can be solved for $y$ : خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = -\tfrac{b^2u}{a^2v}\;x\; + \;\tfrac{b^2}{v}\, .}

باستخدام الاختصارات

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} m &= -\tfrac{b^2u}{a^2v},\\ \color{red}n &= \color{red}\tfrac{b^2}{v} \end{align} }

(I)

and the equation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\color{blue}\tfrac{u^2}{a^2} = 1 - \tfrac{v^2}{b^2} = 1-\tfrac{b^2}{n^2}} } one gets: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle m^2 = \frac{b^4 u^2}{a^4 v^2} = \frac{1}{a^2} {\color{red}\frac{b^4}{v^2}} {\color{blue}\frac{u^2}{a^2}} = \frac{1}{a^2} {\color{red}n^2} {\color{blue}\left(1-\frac{b^2}{n^2}\right)} = \frac{n^2-b^2}{a^2}\, .} Hence

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = \pm\sqrt{m^2 a^2 + b^2}}

(II)

and the equation of a non vertical tangent is خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = m x \pm \sqrt{m^2 a^2 + b^2}.} Solving relations (I) for خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle u,v} and respecting (II) leads to the slope depending parametric representation of the ellipse: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u,v) = \left(-\tfrac{ma^2}{\pm\sqrt{m^2a^2+b^2}}\;,\;\tfrac{b^2}{\pm\sqrt{m^2a^2+b^2}}\right)\, . } (For another proof: see Ellipse#Parametric representation § Notes.)

If a tangent contains the point خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_0,y_0)} , off the ellipse, then the equation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_0 = m x_0 \pm \sqrt{m^2a^2+b^2}} holds. Eliminating the square root leads to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle m^2 - \frac{2x_0y_0}{x_0^2-a^2}m + \frac{y_0^2-b^2}{x_0^2-a^2} = 0,} which has two solutions خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1,m_2} corresponding to the two tangents passing through خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_0,y_0)} . The constant term of a monic quadratic equation is always the product of its solutions. Hence, if the tangents meet at خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_0,y_0)} orthogonally, the following equations hold:

Orthoptics (red circles) of a circle, ellipses and hyperbolas

خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1 m_2 = -1 = \frac{y_0^2 - b^2}{x_0^2 - a^2}} The last equation is equivalent to خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0^2+y_0^2 = a^2+b^2\, .} From (1) and (2) one gets:

The intersection points of orthogonal tangents are points of the circle خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2 + y^2 = a^2 + b^2} .

قطع زائد

The ellipse case can be adopted nearly exactly to the hyperbola case. The only changes to be made are to replace خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle b^2} with خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle -b^2} and to restrict $m$ to $|m| > .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}b/a$ . Therefore:

The intersection points of orthogonal tangents are points of the circle خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2 + y^2 = a^2 - b^2} , where

a > b

.

متعامد مماسات كويكب

Orthoptic (purple) of an astroid

An astroid can be described by the parametric representation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf c(t) = \left(\cos^3t, \sin^3t\right), \quad 0 \le t < 2\pi.} From the condition خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf \dot c(t) \cdot \mathbf \dot c(t+\alpha) = 0} one recognizes the distance $α$ in parameter space at which an orthogonal tangent to $ċ (t)$ appears. It turns out that the distance is independent of parameter $t$ , namely $α = \pm π / 2$ . The equations of the (orthogonal) tangents at the points $c (t)$ and $c (t + π / 2)$ are respectively: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} y &= -\tan t \left(x-\cos^3 t\right) + \sin^3 t, \\ y &= \frac{1}{\tan t} \left(x+\sin^3 t\right) + \cos^3 t. \end{align}} Their common point has coordinates: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} x &= \sin t \cos t \left(\sin t - \cos t\right), \\ y &= \sin t \cos t \left(\sin t + \cos t\right). \end{align}} This is simultaneously a parametric representation of the orthoptic.

Elimination of the parameter $t$ yields the implicit representation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\left(x^2+y^2\right)^3 - \left(x^2-y^2\right)^2 = 0.} Introducing the new parameter $φ = t - 5π / 4$ one gets خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} x &= \tfrac{1}{\sqrt{2}} \cos(2\varphi)\cos\varphi, \\ y &= \tfrac{1}{\sqrt{2}} \cos(2\varphi)\sin\varphi. \end{align}} (The proof uses the angle sum and difference identities.) Hence we get the polar representation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = \tfrac{1}{\sqrt{2}} \cos(2\varphi), \quad 0 \le \varphi < 2\pi} of the orthoptic. Hence:

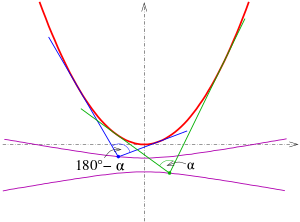
The orthoptic of an astroid is a quadrifolium.

Isoptic of a parabola, an ellipse and a hyperbola

Isoptics (purple) of a parabola for angles 80° and 100°

Isoptics (purple) of an ellipse for angles 80° and 100°

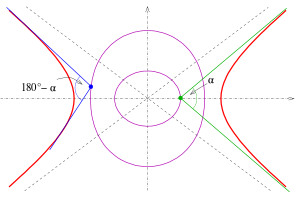
Isoptics (purple) of a hyperbola for angles 80° and 100°

Below the isotopics for angles $α \neq 90°$ are listed. They are called $α$ -isoptics. For the proofs see below.

Equations of the isoptics

Parabola:

The $α$ -isoptics of the parabola with equation $y = ax 2$ are the branches of the hyperbola خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2-\tan^2\alpha\left(y+\frac{1}{4a}\right)^2-\frac{y}{a}=0.} The branches of the hyperbola provide the isoptics for the two angles $α$ and $180° - α$ (see picture).

Ellipse:

The $α$ -isoptics of the ellipse with equation $x 2 / a 2 + y 2 / b 2 = 1$ are the two parts of the degree-4 curve خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(x^2+y^2-a^2-b^2\right)^2 \tan^2\alpha = 4\left(a^2y^2 + b^2x^2 - a^2b^2\right)} (see picture).

Hyperbola:

The $α$ -isoptics of the hyperbola with the equation $x 2 / a 2 - y 2 / b 2 = 1$ are the two parts of the degree-4 curve خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(x^2 + y^2 - a^2 + b^2\right)^2 \tan^2\alpha = 4 \left(a^2y^2 - b^2x^2 + a^2b^2\right).}

البراهين

Parabola:

A parabola $y = ax 2$ can be parametrized by the slope of its tangents $m = 2 ax$ : خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf c(m) = \left(\frac{m}{2a},\frac{m^2}{4a}\right), \quad m \in \R.}

The tangent with slope $m$ has the equation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=mx-\frac{m^2}{4a}.}

The point $(x 0, y 0)$ is on the tangent if and only if خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_0 = m x_0 - \frac{m^2}{4a}.}

This means the slopes $m 1$ , $m 2$ of the two tangents containing $(x 0, y 0)$ fulfil the quadratic equation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle m^2 - 4ax_0m + 4ay_0 = 0.}

If the tangents meet at angle $α$ or $180° - α$ , the equation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan^2\alpha = \left(\frac{m_1-m_2}{1+m_1 m_2}\right)^2}

must be fulfilled. Solving the quadratic equation for $m$ , and inserting $m 1$ , $m 2$ into the last equation, one gets خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0^2-\tan^2\alpha\left(y_0+\frac{1}{4a}\right)^2-\frac{y_0}{a} = 0.}

This is the equation of the hyperbola above. Its branches bear the two isoptics of the parabola for the two angles $α$ and $180° - α$ .

Ellipse:

In the case of an ellipse $x 2 / a 2 + y 2 / b 2 = 1$ one can adopt the idea for the orthoptic for the quadratic equation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle m^2-\frac{2x_0y_0}{x_0^2-a^2}m + \frac{y_0^2-b^2}{x_0^2-a^2} = 0.}

Now, as in the case of a parabola, the quadratic equation has to be solved and the two solutions $m 1$ , $m 2$ must be inserted into the equation خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan^2\alpha=\left(\frac{m_1-m_2}{1+m_1m_2}\right)^2.}

Rearranging shows that the isoptics are parts of the degree-4 curve: خطأ رياضيات (اعرض بصيغة MathML إن أمكن (تحت التجريب): رد غير صحيح ("Math extension cannot connect to Restbase.") من الخادم "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(x_0^2+y_0^2-a^2-b^2\right)^2 \tan^2\alpha = 4\left(a^2y_0^2+b^2x_0^2-a^2b^2\right).}

Hyperbola:

The solution for the case of a hyperbola can be adopted from the ellipse case by replacing $b 2$ with $- b 2$ (as in the case of the orthoptics, see above).

To visualize the isoptics, see implicit curve.

الهامش

المراجع

Lawrence, J. Dennis (1972). A catalog of special plane curves. Dover Publications. pp. 58–59. ISBN 0-486-60288-5.
Odehnal, Boris (2010). "Equioptic Curves of Conic Sections" (PDF). Journal for Geometry and Graphics. 14 (1): 29–43.
Schaal, Hermann (1977). Lineare Algebra und Analytische Geometrie. Vol. III. Vieweg. p. 220. ISBN 3-528-03058-5.
Steiner, Jacob (1867). Vorlesungen über synthetische Geometrie. Leipzig: B. G. Teubner. Part 2, p. 186.
Ternullo, Maurizio (2009). "Two new sets of ellipse related concyclic points". Journal of Geometry. 94 (1–2): 159–173. doi:10.1007/s00022-009-0005-7. S2CID 120011519.

وصلات خارجية

قالب:Differential transforms of plane curves

?