مربع سحري

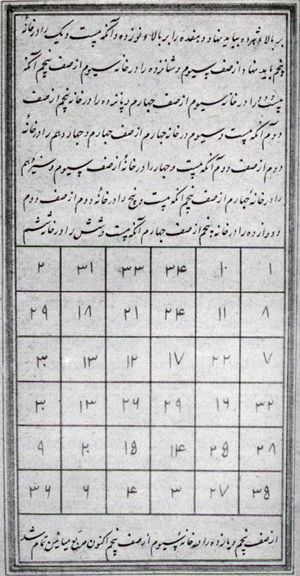
في الرياضيات المسلية، المربع السحري هي مصفوفة مربعة ذات حيز $(n)$، مكونة من $n^{2}$ أعداد صحيحة، بحيث أن حاصل جمع $(n)$ رقم في كلّ من الصفوف والأعمدة والأقطار الرئيسية يأدي لنفس الحاصل. توجد مربعات سحرية مهما كان الحيز $n\geq 1$، بإقصاء $n=2$ (أربع أعداد)، مع كون الحالة $n=1$ تعتبر أمرا بديهيا. يبين الشكل التالي مثالا لمربع سحري من $n=3$

مربع سحري بالفارسية يرجع للقرن السادس عشر الميلادي - من دار الوثائق القومية المصرية.

لاحظ أن مجموع كل سطر وعمود وقطر رئيسي يساوي دائما 15. يسمى هذا المجموع ثابتا سحريا $(M)$ وقيمته بصفة عامة:

$M(n)={\frac {n(n^{2}+1)}{2}}$

قيم الثوابت السحرية لمربعات سحرية عادية ذات حيز $n=5,4,3,\ldots$ هي متتالية: $15,34,65,\ldots$ (البقية).

Magic squares that include repeated entries do not fall under this definition and are referred to as 'trivial'. Some well-known examples, including the Sagrada Família magic square and the Parker square are trivial in this sense. When all the rows and columns but not both diagonals sum to the magic constant this gives a semimagic square (sometimes called orthomagic square).

The mathematical study of magic squares typically deals with their construction, classification, and enumeration. Although completely general methods for producing all the magic squares of all orders do not exist, historically three general techniques have been discovered: by bordering method, by making composite magic squares, and by adding two preliminary squares. There are also more specific strategies like the continuous enumeration method that reproduces specific patterns. Magic squares are generally classified according to their order n as: odd if n is odd, evenly even (also referred to as "doubly even") if n is a multiple of 4, oddly even (also known as "singly even") if n is any other even number. This classification is based on different techniques required to construct odd, evenly even, and oddly even squares. Beside this, depending on further properties, magic squares are also classified as associative magic squares, pandiagonal magic squares, most-perfect magic squares, and so on. More challengingly, attempts have also been made to classify all the magic squares of a given order as transformations of a smaller set of squares. Except for n ≤ 5, the enumeration of higher order magic squares is still an open challenge. The enumeration of most-perfect magic squares of any order was only accomplished in the late 20th century.

Magic squares have a long history, dating back to at least 190 BCE in China. At various times they have acquired occult or mythical significance, and have appeared as symbols in works of art. In modern times they have been generalized a number of ways, including using extra or different constraints, multiplying instead of adding cells, using alternate shapes or more than two dimensions, and replacing numbers with shapes and addition with geometric operations.

Melencolia I (Albrecht Dürer, 1514) includes an order 4 square with magic sum 34

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 التاريخ

Iron plate with an order 6 magic square in Eastern Arabic Numerals from China, dating to the Yuan Dynasty (1271–1368).

Magic squares were known to Chinese mathematicians as early as 650 BC, and explicitly given since 570 AD, and to Islamic mathematicians possibly as early as the seventh century AD. The first magic squares of order 5 and 6 appear in an encyclopedia from Baghdad circa 983, the Encyclopedia of the Brethren of Purity (Rasa'il Ihkwan al-Safa); simpler magic squares were known to several earlier Arab mathematicians. Some of these squares were later used in conjunction with magic letters, as in Shams Al-ma'arif, to assist Arab illusionists and magicians.

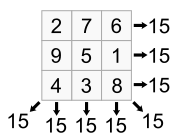
 الصين (Lo Shu square, 3×3 magic square)

4	9	2
3	5	7
8	1	6

The Lo Shu Square, as the magic square on the turtle shell is called, is the unique normal magic square of order three in which 1 is at the bottom and 2 is in the upper right corner. Every normal magic square of order three is obtained from the Lo Shu by rotation or reflection.

 بلاد فارس

Original script from the شمس المعارف.

Printed version of the previous manuscript. Eastern Arabic numerals were used.

 بلاد العرب

Magic squares were known to Islamic mathematicians in Arabia as early as the seventh century. They may have learned about them when the Arabs came into contact with Indian culture and learned Indian astronomy and mathematics – including other aspects of combinatorial mathematics. Alternatively, the idea may have come to them from China. The first magic squares of order 5 and 6 known to have been devised by Arab mathematicians appear in an encyclopedia from Baghdad circa 983, the Rasa'il Ikhwan al-Safa (the Encyclopedia of the Brethren of Purity); simpler magic squares were known to several earlier Arab mathematicians.

The magic square of order three was described as a child-bearing charm since its first literary appearances in the works of Jābir ibn Hayyān (fl. c. 721– c. 815) and al-Ghazālī (1058–1111) and it was preserved in the tradition of the planetary tables, known from H.C.Agrippa's work, too.

The Arab mathematician Ahmad al-Buni, who worked on magic squares around 1250, attributed mystical properties to them, although no details of these supposed properties are known. There are also references to the use of magic squares in astrological calculations, a practice that seems to have originated with the Arabs.

 الهند

Magic Square at the معبد پارشڤاناثا في خاجوراهو بالهند.

The 3×3 magic square has been a part of rituals in India since Vedic times, and still is today. The Ganesh yantra is a 3×3 magic square. There is a well-known 10th-century 4×4 magic square on display في معبد پارشڤاناثا في خاجوراهو، الهند.

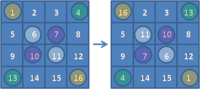
7	12	1	14
2	13	8	11
16	3	10	5
9	6	15	4

This is known as the Chautisa Yantra. Each row, column, and diagonal, as well as each 2×2 sub-square, the corners of each 3×3 and 4×4 square, the corners of each 2×4 and 4×2 rectangle, and the offset diagonals (12+8+5+9, 1+11+16+6, 14+2+3+15 and 7+11+10+6, 12+2+5+15, 1+13+16+4) sum to 34.

In this square, every second diagonal number adds to 17 (the same applies to offset diagonals). In addition to squares and rectangles, there are eight trapeziums – two in one direction, and the others at a rotation of 90 degrees, such as (12, 1, 16, 5) and (13, 8, 9, 4).

These characteristics (which identify it as one of the three 4×4 pandiagonal magic squares and as a most-perfect magic square) mean that the rows or columns can be rotated and maintain the same characteristics - for example:

12	1	14	7
13	8	11	2
3	10	5	16
6	15	4	9

The Kubera-Kolam, a magic square of order three, is commonly painted on floors in India. It is essentially the same as the Lo Shu Square, but with 19 added to each number, giving a magic constant of 72.

23	28	21
22	24	26
27	20	25

 أوروپا

This page from Athanasius Kircher's Oedipus Aegyptiacus (1653) belongs to a treatise on magic squares and shows the Sigillum Iovis associated with Jupiter

In 1514 Albrecht Dürer immortalized a 4×4 square, of order four, in his famous engraving Melencolia I. It is described in more detail below.

Saturn=15
4	9	2
3	5	7
8	1	6

Jupiter=34
4	14	15	1
9	7	6	12
5	11	10	8
16	2	3	13

Mars=65
11	24	7	20	3
4	12	25	8	16
17	5	13	21	9
10	18	1	14	22
23	6	19	2	15

Sol=111
6	32	3	34	35	1
7	11	27	28	8	30
19	14	16	15	23	24
18	20	22	21	17	13
25	29	10	9	26	12
36	5	33	4	2	31

Venus=175
22	47	16	41	10	35	4
5	23	48	17	42	11	29
30	6	24	49	18	36	12
13	31	7	25	43	19	37
38	14	32	1	26	44	20
21	39	8	33	2	27	45
46	15	40	9	34	3	28

Mercury=260
8	58	59	5	4	62	63	1
49	15	14	52	53	11	10	56
41	23	22	44	45	19	18	48
32	34	35	29	28	38	39	25
40	26	27	37	36	30	31	33
17	47	46	20	21	43	42	24
9	55	54	12	13	51	50	16
64	2	3	61	60	6	7	57

Luna=369
37	78	29	70	21	62	13	54	5
6	38	79	30	71	22	63	14	46
47	7	39	80	31	72	23	55	15
16	48	8	40	81	32	64	24	56
57	17	49	9	41	73	33	65	25
26	58	18	50	1	42	74	34	66
67	27	59	10	51	2	43	75	35
36	68	19	60	11	52	3	44	76
77	28	69	20	61	12	53	4	45

The derivation of the sigil of Hagiel, the planetary intelligence of Venus, drawn on the magic square of Venus. Each Hebrew letter provides a numerical value, giving the vertices of the sigil.

S	A	T	O	R
A	R	E	P	O
T	E	N	E	T
O	P	E	R	A
R	O	T	A	S

6	66	848	938
8	11	544	839
1	11	383	839
2	73	774	447

H	E	S	E	B
E	Q	A	L
S
E		G
B

A	D	A	M
D	A	R	A
A	R	A	D
M	A	D	A

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 المربع السحري لألبرشت دورر

تفصيلة من Melencolia I

16	3	2	13
5	10	11	8
9	6	7	12
4	15	14	1

Dürer's magic square can also be extended to a magic cube.

Dürer's magic square and his Melencolia I both also played large roles in Dan Brown's 2009 novel, The Lost Symbol.

 المربع السحري في ساگرادا فاميليا

A magic square on the Sagrada Família church façade

The Passion façade of the Sagrada Família church in Barcelona, conceptualized by Antoni Gaudí and designed by sculptor Josep Subirachs, features a 4×4 magic square:

The magic constant of the square is 33, the age of Jesus at the time of the Passion. Structurally, it is very similar to the Melancholia magic square, but it has had the numbers in four of the cells reduced by 1.

1	14	14	4
11	7	6	9
8	10	10	5
13	2	3	15

While having the same pattern of summation, this is not a normal magic square as above, as two numbers (10 and 14) are duplicated and two (12 and 16) are absent, failing the 1→n² rule.

Similarly to Dürer's magic square, the Sagrada Familia's magic square can also be extended to a magic cube.

This magic square has 24 groups of four fields with the sum of 139 and in the first row - shown at bottom-right - Ramanujan's date of birth.

 المربع السحري لـ سرينيڤاسا رامانوجان

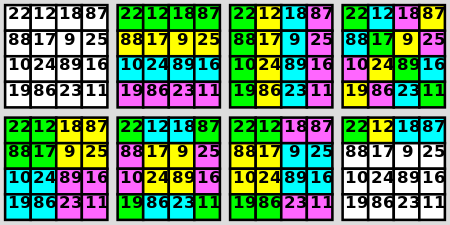
The Indian mathematician Srinivasa Ramanujan created a square where - in addition to several groups of four squares - the first row shows his date of birth, 22nd Dec. 1887.

 بناء المربعات السحرية

هناك العديد من الطرق القديمة والحديثة لبناء مربعات سحرية . يمكن تصنيف المربع السحري إلى ثلاثة أنواع رئيسية:

• مربع سحري ذو رتبة فردية n.
• مربع سحري ذو رتبة زوجية مفردة n (أي ان = n/2 عدد فردي).
• مربع سحري ذو رتبة زوجية مضاعفة n (أي ان = n/2 عدد زوجي).

 طرق إنشاء مربعات سحرية فردية الرتبة

طريقة بناء مربع سحري فردي الرتبة.

تتميز المربعات السحرية فردية الرتبة في إمكانية تدوير المربع حتى تصبح الصفوف والأعمدة أقطارا بينما الأقطار صفوفا وأعمدة. يكون مركز المربع السحري دائما ${\frac {n^{2}+1}{2}}$ تتم العملية بالشكل الاتي:

1- تعبئة المربع بالأرقام 1 حتى n². سيتم تكرار المربع السحري من جميع جوانبه لتسهيل معرفة الأرقام المكملة خارجه عند الإزاحة.

2- قراءة أحد القطرين وليكن القطر الرئيسي ووضعه كعمود وسط المصفوفة الجديدة.

3- قراءة الخلايا الموازية فوق القطر الرئيسي مع إزاحتها خلية واحدة (من الصف والعمود) في كل مرة عن سابقتها نحو اليسار والأعلى. يتم التوقف بعد n-1)/2) خطا موازيا للقطر الرئيسي.

3- قراءة الخلايا الموازية تحت القطر الرئيسي مع إزاحتها خلية واحدة (من الصف والعمود) في كل مرة عن سابقتها نحو اليمين والأسفل. يتم التوقف بعد n-1)/2) خط موازيا للقطر الرئيسي.

4- يتم نقل العناصر الجديدة إلى مصفوفة جديدة مع تدويرها 45 درجة بحيث تصبح الصفوف والأعمدة الأصلية أقطارا والأقطار الأصلية صفوفا.

 طرق إنشاء مربعات سحرية زوجية الرتبة (مضاعفة)

طريقة بناء مربع سحري ذو رتبة زوجية مضاعفة.

تمتاز المربعات السحرية التي يقبل ثابتها السحري القسمة على 4 بدون باقي بإمكانية تطبيق قاعدة التبديل بين المرافقات بعد كل خليتين. يمكن تلخيص العملية كما يلي

1- تعبئة المربع بالأرقام 1 حتى n².

2- التبديل بين جميع أركان المربع. مثلا في المربع 4×4 تكون أركانه هي 1، 4، 13، 16. عند التبديل بين الركن الأول والرابع أي 1، 16 والركن الثاني والثالث أي 4، 13.

3- يتم تكرار الإبدال لكل خليتين متتاليتين (مع ما يقابهما أي التبديل بين كل a_{(n-i+1)(n-j+1)} وa_ji) وترك خليتين أخريين ابتداء من الخلية الثالثة في الصف الأول وحتى الوصول إلى مركز المربع مع عدم المساس بالأركان التي تم تغييرها في الخطوة السابقة.

 طرق إنشاء مربعات سحرية زوجية الرتبة (مفردة)

طريقة بناء مربع سحري ذو رتبة زوجية مفردة.

تعتبر عملية إنشاء المربعات السحرية التي لا تقبل القسمة على 4 بدون باقي صعبة نسبيا، كما أنها لا تتميز بالتماثل التام. أبسط الطرق تتمثل في إعادة تقسيم المربع إلى 4 مربعات صغيرة متكافئة كما يلي:

1- تقسيم المربع إلى 4 مربعات صغيرة متكافئة. لاحظ أن المربعات الناشئة عبارة عن مربعات فردية.

2- تعبئة المربع الأول بالأرقام 1 حتى n²/4.

3- تحويل المربع في الخطوة 2 إلى مربع سحري بالطريقة المستخدمة في المربعات السحرية الفردية.

4- نقل نسخة من هذا المربع في المربعات الثلاثة الباقية مع إضافة n²/4 لكل عنصر في المربع الثاني، n²/2 لكل عنصر في المربع الثالث، و3n²/4 لكل عنصر في المربع الرابع.

5- أصبح المربع السحري جاهزا تقريبا ولكن ينقصه شرط تحقق مجموع عناصر كل قطر. في هذه الحالة يتم التبديل بين بعض عناصر مربعين متجاورين حتى يكتمل الشرط.

 مشاكل رياضية ذات صلة

استخدام عملية الطرح في مكعب من الاعداد من 1 إلى 9

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الخوارزمية

 برمجة المربعات السحرية

حساب المربعات السحرية يصبح سهلا بعد معرفة خوارزمياتها ومن الممكن برمجتها بأي لغة برمجة. مثلا باستعمال متصفح الويب ولغة جافا سكربت يمكن إنشاء دالة المربع السحري لأي عدد طبيعي كما يلي

<html>
<script>
function magic(n)
{
   var i=0, j=(n-1)/2, p, k, m=[],  m1=[], m2=[];
    if(n<=0 || n-Math.ceil(n)!=0) return 'Error: n must be a positive integer..';
    if(n==2) return 'Error: there is no magic square of 2x2 !';
    if(n%4==0){//Double Even
        for (i=0; i<n/2; i++){
            for (j=0; j<n; j++){
                if((((i%4==0)||(i%4==3))&&((j%4==1)||(j%4==2)))||(((j%4==0)||(j%4==3))&&((i%4==1)||(i%4==2)))){
                    m1[j]= i*n+j+1;
                    m2[n-j-1]= n*(n-i)-j;
                }
                else{
                    m1[j]= n*(n-i)-j;
                    m2[n-j-1]=i*n+j+1;
                }            }
            m[i]=m1;
            m[n-i-1]=m2;
            m1=[];
            m2=[];
        }
    }
    else if(n%2==0){//Single Even
        p = n/2;
        m1 = magic(p);
        for (i=0; i<2*p; i++)m[i]=[];
        for (i=0; i<p; i++)for(j=0; j<p; j++){
            m[i][j] = m1[i][j]*1;
            m[i][j+p] = m1[i][j]*1+2*p*p;
            m[i+p][j] = m1[i][j]*1+3*p*p;
            m[i+p][j+p] = m1[i][j]*1+p*p;
         }
        for(i=0; i<p; i++){
            k = (n-2)/4;
            for(j=0; j<k; j++){
                k2=m[i][j];
                m[i][j]=m[i+p][j];
                m[i+p][j]=k2;
            }
        }
        for(i=0; i<p; i++){
            for(j=n-k+1; j<n; j++){
                k2=m[i][j];
                m[i][j]=m[i+p][j];
                m[i+p][j]=k2;
            }
        }
        k2=m[k][0]; m[k][0]=m[k+p][0]; m[k+p][0]=k2;
        k2=m[k][k]; m[k][k]=m[k+p][k]; m[k+p][k]=k2;
    }
    else{// Odd
        for (k=1; k<=n*n; k++)
        {
            m2[i*n +j] = k;
            i--;
            j++;
            if (k%n == 0){
                i += 2;
                j--;
            }
            if (j==n)j = 0;
            if (i==-1) i = n-1;
        }
        for(i=0;i<n;i++){for(j=0;j<n;j++)m1[j]=m2[i*n+j];m[i]=m1;m1=[];}
    }
    m[0][0]=' '+m[0][0];
    for (k=0; k<n; k ++) m[k][n-1] += '\n';
    return m;
}
</script>
<noscript> Java script must be enabled..<br /> </noscript>
<body>
Magic square of <input id=ent value="6">
<input type="button" value = " = " onclick ="disp.value=magic(ent.value*1)">
<br /><textarea id="disp" style="width: 780px; height: 300px">
</textarea>
</body>
</html>

 تطبيقات

للمربع السحري بعض التطبيقات المسلية والعلمية أحيانا. يمكن بواسطته مثلا تحليل المساحات بشكل منتظم. مثال ذلك المسألة التالية:

لو كان لدينا 81 قطعة ذهبية بحيث أن كتلة كل قطعة تساوي ترتيبها. أي أن كتلة الأولى 1 غرام والثانية 2 غرام وهكذا وتطلب الأمر توزيعها بشكل عادل بين 9 أفراد. نلاحظ أن إعادة توزيع هذه القطع في مربع سحري 9×9 يعطي الحل الأمثل بحيث يصبح نصيب كل فرد أحد صفوف المربع. يمكن أيضا توزيعها بطريقة الأعمدة بحيث يكون نصيب كل فرد أحد أعمدة المربع السحري.

 المربعات السحرية في الثقافة الشعبية

Macau stamps featuring magic squares

On October 9, 2014 the post office of Macao in the People's Republic of China issued a series of stamps based on magic squares. The figure below shows the stamps featuring the nine magic squares chosen to be in this collection.

The metallic artifact at the center of the X-Files episode Biogenesis is alleged by Chuck Burks to be a magic square.

Mathematician Matt Parker attempted to create a 3x3 magic square using square numbers in a YouTube video on the Numberphile channel. His failed attempt is known as the Parker Square.

 انظر أيضاً

• Antimagic square
• Arithmetic sequence
• Combinatorial design
• Freudenthal magic square
• John R. Hendricks
• Hexagonal tortoise problem
• Latin square
• Magic15 - A game using a 3-by-3 magic square
• Magic circle
• Magic cube classes
• Magic series
• Most-perfect magic square
• Nasik magic hypercube
• Prime reciprocal magic square
• Room square
• Square matrices
• Sriramachakra
• سودوكو
• Unsolved problems in mathematics
• Vedic square

 وصلات خارجية

• Eaves, Laurence (2009). "Magic Square". Sixty Symbols. Brady Haran for the University of Nottingham.
• مربع سحري at the Open Directory Project