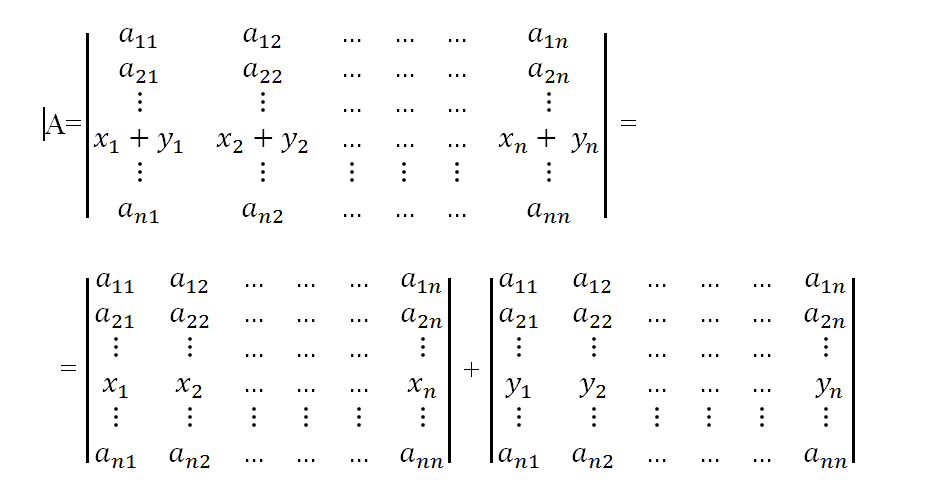محدد
في الجبر الخطي، المحدد determinant هو دالة رياضية تعتمد على العدد n و يربط قيمة قياسية scalar هي det(A) بكل مصفوفة مربعة n×n .
المعنى الهندسي الأساسي للمحدد هو انه بمثابة عامل المقياس للحجم عندما يعتبر A تحويلا خطيا . المحددات مهمة جدا في التحليل الرياضي (قاعدة الاستبدال) و الجبر الخطي المتعدد multilinear algebra .
يرمز عادة لمحدد مصفوفة ما A بالرمز |A|
انواع المحددات
بداية لا يمكن حساب المحدد إلا للمصفوفة المربعة ويكون المحدد بحسب ابعاد المصفوفة فإن كانت المصفوفة المربعة ذات بعد n يكون المحدد من المرتبة n , ويعطي المحدد قيمة عددية للمصفوفة المقابلة
حساب المحددات
- حساب المحدد من المرتبة الاولى يملك نفس قيمة العنصر الوحيد للمصفوفة المقابلة
- حساب المحدد من المرتبة الثانية ويكون وفق القانون :
A=
- حساب المحدد من المرتبة الثالثة :
- طريقة ساروس :
- طريقة النجمة :
الخطوات : الخطوة الأولى :
نأخذ عناصر القطر الرئيسي ونصل بينها بخط ...
ثم نأخذ العنصر الموجود في الزاوية اليمينية العليا وهو a_13 ونصله بخط مع العنصر a_32
ثم نصل بخط بين العنصرين a_32 و a_21
ثم نصل بين a_21 و a_13 كي نشكل مثلثاً ..
وأيضاً نشكل مثلثاً آخر بنفس الطريقة
نصل بين a_31 مع a_12 وبين a_12 مع a_23
ثمَّ بين a_23 مع ئ_31
نأخذ كل 3 عناصر موصولة بخط واحد أو مثلث واحد ونحسب جداءها ونجمع الجداءات
أي (a11 * a22 * a33)+(a13 * a21 * a32)+(a31 * a12 * a23)
الخطوة الثانية : نأخذ عناصر القطر الثانوي ونصل بينها بخط ... ثم نأخذ العنصر الموجود في الزاوية اليسارية العليا وهو a_11 ونصله بخط مع العنصر a_23 ثم نصل بخط بين العنصرين a_23 و a_32 ثم نصل بين a_32 و a_11 كي نشكل مثلثاً ..
ونشكل مثلثاً آخر بنفس الطريقة نصل بين 33 a مع a21 وبين a21 مع a12 ثمَّ بين a12 مع a33 أيضاً نأخذ كل 3 عناصر موصولة بخط واحد أو مثلث واحد ونحسب جداءها ونطرح الجداءات من الناتج السابق أي: - (a13 * a22 * a31) – (a11 * a23 * a32) – (a12 * a21 * a33) بجمع المقدارين ينتج لدينا قيمة المحدد ...
مثال : احسب قيمة المحدد التالي : A=
الحل :
بحسب طريقة ساروس نأخذ العمودين الأول والثاني ونضعهما على يمين العمود الثالث .. ثم نكمل الحساب كما في السابق :
|A|= 3 + 0 + 6 - 6 - 5 – 0 = - 2
2- طريقة النجمة : ( 3 + 6 + 0 ) + (-6 -5 -0) = -2
- حساب المحددات من المرتبة n
لتكن A=[a_ij ] مصفوفة مربعة من المرتبة n محددها هو |A| ندعو المحدد |Aij| والناتج من حذف السطر i والعمود j في المحدد |A| بصغير العنصر aij من المصفوفة A وندعو بالمتمم الجبري للعنصر aij من المصفوفة A
إن Aij هي المتممات الجبرية للمصفوفة [A=[a_ij من أجل جميع : i= 1, 2, ……n j = 1,2,…….n
يمكن حساب قيمة المحدد |A| من المرتبة n بنشره وفق عناصر السطر i كما يلي :
|A| = ai1 . Ai1 + ai2 . Ai2 + ai3 .Ai3 + ……………+ ain. Ain
تعريف: لتكن A مصفوفة مربعة من المرتبة n أي أنَّ :
ندعو الرمز |A| أو det A بمحدد المصفوفة A من المرتبة n ونكتب :
det A = = =
مثال :
=
أنواع المحددات :
- المحدد من المرتبة الأولى :
= ===>
- المحدد من المرتبة الثانية :
خواص المحددات
1.إن |A|=|At| إي أنه :إذا بدلنا في مواقع الأسطر والأعمدة فإن المحدد للمصفوفة A لا تتغير قيمته أي جعلنا الأسطر أعمدة والأعمدة أسطر فإن قيمة المحدد لا تتغير وكل خاصة صحيحة من أجل الأعمدة صحيحة من أجل الأسطر والعكس صحيح .
مثال :
|A| =
|At| =
2.إذا بدلنا بين موضعي سطرين (أو عمودين ) في المحدد |A| فإن قيمة هذا المحدد لا تتغير ولكـــن :: تكون مخالفة بالإشارة
3.إذا كانت جميع عناصر أحد الأسطر (أو أحد الأعمدة ) في محدد ما تساوي الصفر فإن قيمة هذا المحدد تكون معدومة .
مثال
|A|=
لأن العمود الاول كله اصفار.
4.إذا وُجِدَ في محدد سطرين (أو عمودين) متماثلين فإن قيمة هذا المحدد تكون مساوية للصفر .
5.إذا وُجِدَ في محدد سطران متناسبان (أو عمودان متناسبان) فإن قيمة هذا المحدد تساوي الصفر
مثال
|A|= = 18 - 6 - 18 – 18 + 18 + 6 =0
لوجود سطرين متناسبين
6.محدد مصفوفة مثلثية سفلية ( أو علوية ) يساوي إلى جداء عناصر قطرها الرئيسي
مثال :
|A|=
7.إذا كانت جميع عناصر سطر ما أو عمود ما في محدد عبارة عن مجموع عنصرين فإن هذا المحدد يفرق إلى مجموع محددين .
أي : إذا كان السطر i يكتب بالشكل
فإن المحدد |A| يكتب بالشكل :
مثال :
A=
=
= +
8.إذا ضربنا أحد الأسطر{ جميع عناصر هذا السطر } (أو أحد الأعمدة ) في محدد ما بعدد ثابت غير معدوم فإن قيمة هذا المحدد تكون مضروبة بهذا العدد.
مثال :
|A| =
|A| =3*
9.قيمة محدد المصفوفة الواحدية هو الواحد
10.لا تتغير قيمة المحدد إذا أضفنا أو طرحنا إلى أحد عناصر أسطره (أو أحد عناصر أعمدته ) العناصر المقابلة لها من سطر آخر ( أو عمود آخر ) بعد ضربها بعدد ما لا يساوي الصفر .
مثال احسب قيمة المحدد التالي :
الحل : نستخدم الطريقة المباشرة ننشر حسب السطر الثاني لوجود صفر فيه
انظر أيضاً
الهامش
المراجع
- Anton, Howard (2005), Elementary Linear Algebra (Applications Version) (9th ed.), Wiley International
- Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.
- Bareiss, Erwin (1968), "Sylvester's Identity and Multistep Integer-Preserving Gaussian Elimination", Mathematics of Computation 22 (102): 565–578, doi:, https://www.ams.org/journals/mcom/1968-22-103/S0025-5718-1968-0226829-0/S0025-5718-1968-0226829-0.pdf
- de Boor, Carl (1990), "An empty exercise", ACM SIGNUM Newsletter 25 (2): 3–7, doi:, http://ftp.cs.wisc.edu/Approx/empty.pdf
- Bourbaki, Nicolas (1998), Algebra I, Chapters 1-3, Springer, ISBN 9783540642435
- Bunch, J. R.; Hopcroft, J. E. (1974). "Triangular Factorization and Inversion by Fast Matrix Multiplication". Mathematics of Computation. 28 (125): 231–236. doi:10.1090/S0025-5718-1974-0331751-8. hdl:1813/6003.
- Dummit, David S.; Foote, Richard M. (2004), Abstract algebra (3rd ed.), Hoboken, NJ: Wiley, ISBN 9780471452348, OCLC 248917264
- Fisikopoulos, Vissarion; Peñaranda, Luis (2016), "Faster geometric algorithms via dynamic determinant computation", Computational Geometry 54: 1–16, doi:
- Garibaldi, Skip (2004), "The characteristic polynomial and determinant are not ad hoc constructions", American Mathematical Monthly 111 (9): 761–778, doi:
- Habgood, Ken; Arel, Itamar (2012). "A condensation-based application of Cramer's rule for solving large-scale linear systems" (PDF). Journal of Discrete Algorithms. 10: 98–109. doi:10.1016/j.jda.2011.06.007. Archived (PDF) from the original on 2019-05-05.
- Harris, Frank E. (2014), Mathematics for Physical Science and Engineering, Elsevier, ISBN 9780128010495
- Kleiner, Israel (2007), Kleiner, Israel, ed., A history of abstract algebra, Birkhäuser, doi:, ISBN 978-0-8176-4684-4
- Kung, Joseph P.S.; Rota, Gian-Carlo; Yan, Catherine (2009), Combinatorics: The Rota Way, Cambridge University Press, ISBN 9780521883894
- Lay, David C. (August 22, 2005), Linear Algebra and Its Applications (3rd ed.), Addison Wesley, ISBN 978-0-321-28713-7
- Lombardi, Henri; Quitté, Claude (2015), Commutative Algebra: Constructive Methods, Springer, ISBN 9789401799447
- Mac Lane, Saunders (1998), Categories for the Working Mathematician, Graduate Texts in Mathematics 5 (2nd ed.), Springer-Verlag, ISBN 0-387-98403-8
- Meyer, Carl D. (February 15, 2001), Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8, http://www.matrixanalysis.com/DownloadChapters.html
- Muir, Thomas (1960), A treatise on the theory of determinants, Revised and enlarged by William H. Metzler, New York, NY: Dover
- Poole, David (2006), Linear Algebra: A Modern Introduction (2nd ed.), Brooks/Cole, ISBN 0-534-99845-3
- G. Baley Price (1947) "Some identities in the theory of determinants", American Mathematical Monthly 54:75–90 MR 0019078
- Horn, Roger Alan; Johnson, Charles Royal (2018) [1985]. Matrix Analysis (2nd ed.). Cambridge University Press. ISBN 978-0-521-54823-6.
- Lang, Serge (1985), Introduction to Linear Algebra, Undergraduate Texts in Mathematics (2 ed.), Springer, ISBN 9780387962054
- Lang, Serge (1987), Linear Algebra, Undergraduate Texts in Mathematics (3 ed.), Springer, ISBN 9780387964126
- Lang, Serge (2002). Algebra. Graduate Texts in Mathematics. New York, NY: Springer. ISBN 978-0-387-95385-4.
- Leon, Steven J. (2006), Linear Algebra With Applications (7th ed.), Pearson Prentice Hall
- Rote, Günter (2001), "Division-free algorithms for the determinant and the Pfaffian: algebraic and combinatorial approaches", Computational discrete mathematics, Lecture Notes in Comput. Sci., 2122, Springer, pp. 119–135, doi:, ISBN 978-3-540-42775-9
- Trefethen, Lloyd; Bau III, David (1997), Numerical Linear Algebra (1st ed.), Philadelphia: SIAM, ISBN 978-0-89871-361-9
Historical references
- Bourbaki, Nicolas (1994), Elements of the history of mathematics, Springer, doi:, ISBN 3-540-19376-6
- Cajori, Florian (1993), A history of mathematical notations: Including Vol. I. Notations in elementary mathematics; Vol. II. Notations mainly in higher mathematics, Reprint of the 1928 and 1929 originals, Dover, ISBN 0-486-67766-4
- Bézout, Étienne (1779), Théorie générale des equations algébriques, Paris, https://gallica.bnf.fr/ark:/12148/bpt6k106053p.image
- Cayley, Arthur (1841), "On a theorem in the geometry of position", Cambridge Mathematical Journal 2: 267–271
- Cramer, Gabriel (1750), Introduction à l'analyse des lignes courbes algébriques, Genève: Frères Cramer & Cl. Philibert, doi:
- Eves, Howard (1990), An introduction to the history of mathematics (6 ed.), Saunders College Publishing, ISBN 0-03-029558-0
- Grattan-Guinness, I., ed. (2003), Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences, 1, Johns Hopkins University Press, ISBN 9780801873966
- Jacobi, Carl Gustav Jakob (1841), "De Determinantibus functionalibus", Journal für die reine und angewandte Mathematik 1841 (22): 320–359, doi:, https://www.digizeitschriften.de/dms/img/?PID=GDZPPN002142724&physid=phys325#navi
- Laplace, Pierre-Simon, de (1772), "Recherches sur le calcul intégral et sur le systéme du monde", Histoire de l'Académie Royale des Sciences (Paris) (seconde partie): 267–376, https://gallica.bnf.fr/ark:/12148/bpt6k77596b/f374
وصلات خارجية
- قالب:SpringerEOM
- Eric W. Weisstein, Determinant at MathWorld.
- O'Connor, John J.; Robertson, Edmund F., "Matrices and determinants", MacTutor History of Mathematics archive, University of St Andrews.
- Determinant Interactive Program and Tutorial
- Linear algebra: determinants. Archived 2008-12-04 at the Wayback Machine Compute determinants of matrices up to order 6 using Laplace expansion you choose.
- Determinant Calculator Calculator for matrix determinants, up to the 8th order.
- Matrices and Linear Algebra on the Earliest Uses Pages
- Determinants explained in an easy fashion in the 4th chapter as a part of a Linear Algebra course.





![{\displaystyle A=[a_{ij}]_{n}}](https://www.marefa.org/api/rest_v1/media/math/render/svg/e46f66eb35051503d96049907a0a4f85e0dd7cad)







![{\displaystyle A=[a_{11}]}](https://www.marefa.org/api/rest_v1/media/math/render/svg/49387875728d921dde40ed24c7cde1f46cf34f92)