نرد
النرد Dice هو شكل مكعب يستخدم في الألعاب عندما تكون النتائج المطلوبة عشوائية.
يصنع النرد من البلاستك أو الخشب أو المعدن او الحجر, ترقم وجوهه بأرقام من 1-6 أي 1, 2, 3, 4, 5, 6.
يمكن أن يكون النرد بشكل آخر غير المكعب وكما هو مبين بالصورة ولكن الشكل المكعب هو الغالب.
تنويعات
غير رقمية
غير مكعبة
تنويعات قياسية
| Sides | Shape | Notes | |
|---|---|---|---|
| 4 | tetrahedron | Each face has three numbers: they are arranged such that the upright number (which counts) is the same on all three visible faces. Alternatively, all of the sides have the same number in the lowest edge and no number on the top. This die does not roll well and thus it is usually thrown into the air instead. | |
| 6 | cube | A common die. The sum of the numbers on opposite faces is seven. | |
| 8 | octahedron | Each face is triangular; looks like two square pyramids attached base-to-base. Usually, the sum of the opposite faces is 9. | |
| 10 | pentagonal trapezohedron | Each face is a kite. The die has two sharp corners, where five kites meet, and ten blunter corners, where three kites meet. The ten faces usually bear numbers from zero to nine, rather than one to ten (zero being read as "ten" in many applications). Often all odd numbered faces converge at one sharp corner, and the even ones at the other. The sum of the numbers on opposite faces is usually 9 (numbered 0–9) or 11 (number 1–10). | |
| 12 | dodecahedron | Each face is a regular pentagon. The sum of the numbers on opposite faces is usually 13. | |
| 20 | icosahedron | Faces are equilateral triangles. A 2nd century AD Roman icosahedron die is in the collection of the المتحف البريطاني, though the game for which it was used is not known.[1] These are sometimes numbered 0–9 twice as an alternative to 10-sided dice. The sum of the numbers on opposite faces is 21 if numbered 1–20. | |
تنويعات أكثر ندرة
| Sides | Shape | Notes |
|---|---|---|
| 1 | sphere | Most commonly a joke die,[citation needed] this is just a sphere with a 1 marked on it. About spherical dice that may produce more than one result, see the section non-cubical dice above. See also Monostatic polytope, Gömböc. |
| 2 | cylinder | This is nothing more than a coin shape with 1 marked on one side and 2 on the other. While some tasks in roleplaying require flipping a coin, the game rules usually simply call for the use of a coin rather than requiring the use of a two-sided die. It is possible, however, to find dice of this sort for purchase, but they are rare, and can typically be found among other joke dice. |
| 3 | Rounded-off triangular prism | This is a rounded-off triangular prism, intended to be rolled like a rolling-pin style die. The die is rounded-off at the edges to make it impossible for it to somehow land on the triangular sides, which makes it look a bit like a jewel. When the die is rolled, one edge (rather than a side) appears facing upwards. On either side of each edge the same number is printed (from 1 to 3). The numbers on either side of the up-facing edge are read as the result of the die roll. Another possible shape is the "American Football" or "Rugby ball" shape, where the ends are pointed (with rounded points) rather than just rounded. A third variety features faces that resemble warped squares. |
| 5 | Triangular prism | This is a prism that is thin enough to land either on its "edge" or "face". When landing on an edge, the result is displayed by digits (2–4) close to the prism's top edge. The triangular faces are labeled with the digits 1 and 5. |
| 7 | Pentagonal prism | Similar in constitution to the 5-sided die. When landing on an edge, the topmost edge has pips for 1–5. The pentagonal faces are labeled with the digits 6 and 7. This kind of die is particularly odd since it has pips for five of its results and digits for two of them. Seven-sided dice are used in a seven-player variant of backgammon. Some variants have heptagonal ends and rectangular faces. |
| 12 | rhombic dodecahedron | Each face is a rhombus. |
| 14 | heptagonal trapezohedron | Each face is a kite. |
| 16 | octagonal dipyramid | Each face is an isosceles triangle. |
| 24 | tetrakis hexahedron | Each face is an isosceles triangle. |
| 24 | deltoidal icositetrahedron | Each face is a kite. |
| 30 | rhombic triacontahedron | Each face is a rhombus. Although not included in most dice kits, it can be found in most hobby and game stores. |
| 34 | heptadecagonal trapezohedron | Each face is a kite. |
| 50 | icosakaipentagonal trapezohedron | The faces of the 50-sided die are kites, although very narrow. |
| 60 | pentakis dodecahedron | |
| 100 | Zocchihedron | 100-sided dice can be found in hobby and game stores. They are not, however, a true polyhedron. A 100-sided die is made by flattening 100 facets on a sphere. |
The full geometric set of "uniform fair dice" (face-transitive) are:
- Platonic solids, the five regular polyhedra: 4, 6, 8, 12, 20 sides
- Catalan solids, the duals of the 13 Archimedean solids: 12, 24, 30, 48, 60, 120 sides
- Bipyramids, the duals of the infinite set of prisms, with triangle faces: any even number above 4
- Trapezohedrons, the duals of the infinite set of antiprisms, with kite faces: any even number above 4
- Disphenoids, an infinite set of tetrahedra made from congruent non-regular triangles: 4 sides
- "Rolling-pin style dice" are the only way to make dice with an odd number of flat faces.[2] They are based on an infinite set of prisms. All the (rectangular) faces they may actually land on are congruent, so they are equally fair. (The other 2 sides of the prism are rounded or capped with a pyramid, designed so that the die never actually rests on those faces.)
الاحتمالات
For a single roll of a fair s-sided die, the probability of rolling each value is exactly 1/s; this is an example of a discrete uniform distribution. For n multiple rolls, with a s-sided die the possibility space is equal to sn. So, for n rolls of an s-sided die the probability of any result is 1/sn.
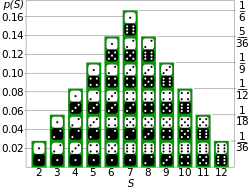
However, if we are rolling two dice and adding the result together, as in the game craps, the total is distributed in a triangular curve; the case for common dice follows:
| Sum | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Probability | 1/36 |
2/36 =1/18 |
3/36 =1/12 |
4/36 =1/9 |
5/36 |
6/36 =1/6 |
5/36 |
4/36 =1/9 |
3/36 =1/12 |
2/36 =1/18 |
1/36 |
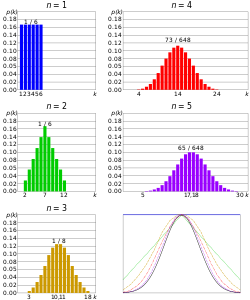
As the number of dice increases, the distribution of the sum of all numbers tends to normal distribution by the central limit theorem; the exact value of a sum of n s-sided dice, k, is
where Fs,1(k) = 1/s for 1 ≤ k ≤ s and 0 otherwise.
A faster algorithm would adapt the exponentiation by squaring algorithm:
.
In the triangular curve described above,
Equivalently, the probability can be calculated using combinations:
where is the floor function. The probability of rolling an exact sequence of numbers is 1/sn.
تطبيقات ألعاب اتخاذ أدوار
ألعاب النرد
- الطاولة (النرد).
- المونوبولي Monopoly.
- الحية والسلم Snakes and Ladders.
انظر أيضاً

- Barrel die
- Crown and Anchor
- d20 system
- Dreidel
- Fuzzy dice
- Musikalisches Würfelspiel
- Nontransitive dice
- Sicherman dice
- Teetotum
- Urim and Thummim
الهامش
- ^ Thompson, Clive (December 2, 2003). "Ancient Roman dungeonmastering". Collision Detection. Retrieved 2006-06-26.
- ^ "Properties of Dice" (PDF). http://www.aleakybos.ch. Retrieved 2012-10-07.
{{cite web}}: External link in|publisher=
وصلات خارجية
- Eric W. Weisstein, Dice at MathWorld. Analysis of dice probabilities, also features Uspenski's work on rolling multiple dice.
- Mathematically "Fair Dice"
- "Fair Dice" is an illustrated Math Games column about all the possible fair dice, and the mathematical reasons why other shapes are not fair.
- A complete list of all possible Fair Dice which has nice illustrations
- Animation clearly demonstrating the probability space of dice
- World's Largest Dice Collection Links, Photos, Information about dice
- Computer Simulation of Irregular Dice
- "A Pair of Dice Which Never Roll 7"
- The oldest backgammon set found in Iran
- "A Brief History of Dice" (in Dungeons & Dragons games)
- "How do you make loaded dice?", The Straight Dope, July 14, 2009
- A discussion linking dice and Tarot cards
- "Why Dice Behave the Way They Do", Popular Science July 1945
- Dice size chart shows common dice dimensions
- "Dice – A Dicey Love Affair" A list of board games with special dice




![{\displaystyle {\begin{aligned}F_{6,2}(6)&=\sum _{n}{F_{6,1}(n)F_{6,1}(6-n)}\\&=F_{6,1}(1)F_{6,1}(5)+F_{6,1}(2)F_{6,1}(4)+\\&\qquad \cdots +F_{6,1}(5)F_{6,1}(1)\\[6pt]&=5\cdot {\frac {1}{6}}\cdot {\frac {1}{6}}={\frac {5}{36}}\approx 0.14\end{aligned}}}](https://www.marefa.org/api/rest_v1/media/math/render/svg/4c9b756a49df9ad4accd725d57b13b3eacfea61d)

