مسألة P=NP

مسائل جوائز الألفية
	نظرية التعقيد
	حدسية هودج
	حدسية پوانكاريه
	فرضية ريمان
	وجود يانگ-ميلز وفجوة الكتلة
	معادلات ناڤييه-ستوكس
	حدسية بيرش وسوينرتون-داير
	عدل

الصفحة قالب:Unsolved/styles.css ليس بها محتوى.

مسألة غير محلولة في computer science:

If the solution to a problem is easy to check for correctness, must the problem be easy to solve?

العلاقة بين مسائل التعقيد P و مسائل NP الكاملة هي مسألة غير محلولة في المعلوماتية النظرية. وهي تعتبر من أهم المسائل في هذا الحقل وقد عرض معهد كلاي للرياضيات جائزة مقدارها مليون دولار أمريكي لأول برهان صحيح لهذه المسألة.

جوهر المسألة في أنه إذا كان من الممكن التأكد من الجواب الصحيح لمسألة ما بعد الحصول عليه في الزمن الخطي فهل من الممكن أيضاً حساب هذه الأجوبة ذاتها بسرعة؟

خذ على سبيل المثال مسألة مجموع المجموعات الجزئية، وهو مثال على مسألة من السهل التحقق من صحة جوابها، لكن عملية حساب الجواب نفسه يعتبر (هذا الأمر غير مبرهن بعد) من الأمور الصعبة. على سبيل المثال هل يوجد مجموعة جزئية من المجموعة التالية {−2, −3, 15, 14, 7, −10} يكون مجموع عناصرها مساوياً للصفر؟ الجواب بكل بساطة هو نعم، لأن المجموعة الجزئية {−2, −3, −10, 15} مجموعها صفر وهو أمر من الممكن التحقق منه بكل بساطة بجمع العناصر. لكن إن عملية إيجاد كل مجموعة جزئية من المجموعة الأساسية يكون مجموع جميع عناصرها ينتهي إلى الصفر يأخذ وقتاً طويلاً.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

NP-completeness

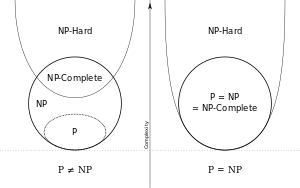
Euler diagram for P, NP, NP-complete, and NP-hard set of problems (excluding the empty language and its complement, which belong to P but are not NP-complete)

مقال رئيسي: NP-completeness

مسائل في NP غير معروف إذا كانت في P أو في NP-complete

مقال رئيسي: NP-intermediate

In 1975, Richard E. Ladner showed that if P ≠ NP, then there exist problems in NP that are neither in P nor NP-complete.^[1] Such problems are called NP-intermediate problems. The graph isomorphism problem, the discrete logarithm problem, and the integer factorization problem are examples of problems believed to be NP-intermediate. They are some of the very few NP problems not known to be in P or to be NP-complete.

The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic. An important unsolved problem in complexity theory is whether the graph isomorphism problem is in P, NP-complete, or NP-intermediate. The answer is not known, but it is believed that the problem is at least not NP-complete.^[2] If graph isomorphism is NP-complete, the polynomial time hierarchy collapses to its second level.^[3] Since it is widely believed that the polynomial hierarchy does not collapse to any finite level, it is believed that graph isomorphism is not NP-complete. The best algorithm for this problem, due to László Babai, runs in quasi-polynomial time.^[4]

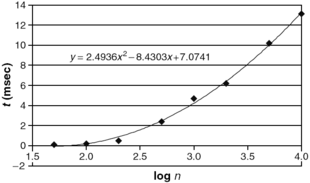
The integer factorization problem is the computational problem of determining the prime factorization of a given integer. Phrased as a decision problem, it is the problem of deciding whether the input has a factor less than k. No efficient integer factorization algorithm is known, and this fact forms the basis of several modern cryptographic systems, such as the RSA algorithm. The integer factorization problem is in NP and in co-NP (and even in UP and co-UP^[5]). If the problem is NP-complete, the polynomial time hierarchy will collapse to its first level (i.e., NP = co-NP). The most efficient known algorithm for integer factorization is the general number field sieve, which takes expected time

O\left(\exp \left(\left({\tfrac {64n}{9}}\log(2)\right)^{\frac {1}{3}}\left(\log(n\log(2))\right)^{\frac {2}{3}}\right)\right)

to factor an n-bit integer. However, the best known quantum algorithm for this problem, Shor's algorithm, does run in polynomial time, although this does not indicate where the problem lies with respect to non-quantum complexity classes.

هل P تعني "سهلة"؟

The graph shows the running time vs. problem size for a knapsack problem of a state-of-the-art, specialized algorithm. The quadratic fit suggests that the algorithmic complexity of the problem is O((log(n))²).^[6]

All of the above discussion has assumed that P means "easy" and "not in P" means "difficult", an assumption known as Cobham's thesis. It is a common and reasonably accurate^{[بحاجة لمصدر]} assumption in complexity theory; however, it has some caveats.

انظر أيضاً

ملاحظات

المراجع

^ خطأ استشهاد: وسم <ref> غير صحيح؛ لا نص تم توفيره للمراجع المسماة Ladner75
^ Arvind, Vikraman; Kurur, Piyush P. (2006). "Graph isomorphism is in SPP". Information and Computation. 204 (5): 835–852. doi:10.1016/j.ic.2006.02.002.
^ Schöning, Uwe (1988). "Graph isomorphism is in the low hierarchy". Journal of Computer and System Sciences. 37 (3): 312–323. doi:10.1016/0022-0000(88)90010-4.
^ Babai, László (2018). "Proceedings of the International Congress of Mathematicians—Rio de Janeiro 2018. Vol. IV. Invited lectures".: 3319–3336, World Sci. Publ., Hackensack, NJ.
^ Lance Fortnow. Computational Complexity Blog: Complexity Class of the Week: Factoring. 13 September 2002.
^ Pisinger, D. 2003. "Where are the hard knapsack problems?" Technical Report 2003/08, Department of Computer Science, University of Copenhagen, Copenhagen, Denmark

المصادر

Rachel Crowell (28 May 2021). "The Top Unsolved Questions in Mathematics Remain Mostly Mysterious Just one of the seven Millennium Prize Problems named 21 years ago has been solved". www.scientificamerican.com. Retrieved 21 June 2021. This problem concerns the issue of whether questions that are easy to verify (a class of queries called NP) also have solutions that are easy to find (a class called P).
Hosch, William L (11 August 2009). "P versus NP problem mathematics". Encyclopædia Britannica. Retrieved 20 June 2021.
"P vs NP Problem". www.claymath.org (Cook, Levin). Retrieved 20 June 2021. Suppose that you are organizing housing accommodations for a group of four hundred university students. Space is limited and only one hundred of the students will receive places in the dormitory. To complicate matters, the Dean has provided you with a list of pairs of incompatible students, and requested that no pair from this list appear in your final choice. This is an example of what computer scientists call an NP-problem...

للاستزادة

Cormen, Thomas (2001). Introduction to Algorithms. Cambridge: MIT Press. ISBN 978-0-262-03293-3.
Garey, Michael; Johnson, David (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. San Francisco: W. H. Freeman and Company. ISBN 978-0-7167-1045-5.
Goldreich, Oded (2010). P, NP, and NP-Completeness. Cambridge: Cambridge University Press. ISBN 978-0-521-12254-2. Online drafts
Immerman, N. (1987). "Languages that Capture Complexity Classes". SIAM Journal on Computing. 16 (4): 760–778. CiteSeerX 10.1.1.75.3035. doi:10.1137/0216051.
Papadimitriou, Christos (1994). Computational Complexity. Boston: Addison-Wesley. ISBN 978-0-201-53082-7.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .