محل هندسي

في الرياضيات، يطلق اسم المحل الهندسي إنگليزية: locus على مجموعة النقاط التي تشترك بخاصية معينة. على سبيل المثال المستقيم هو المحل الهندسي لمجموعة النقاط المتساوية البعد عن مستقيمين متوازيين.
أمثلة في الهندسة المستوية
- الدائرة هي المحل الهندسي للنقاط المتساوية البعد عن نقطة مركز الدائرة.
- قطع مكافئ: the set of points equidistant from a fixed point (the focus) and a line (the directrix).
- Hyperbola: the set of points for each of which the absolute value of the difference between the distances to two given foci is a constant.
- القطع الناقص هو المحل الهندسي للنقاط التي تكون مجموع بعديها عن نقطتي المحرق متساوية.
Other examples of loci appear in various areas of mathematics. For example, in complex dynamics, the Mandelbrot set is a subset of the complex plane that may be characterized as the connectedness locus of a family of polynomial maps.
برهان محل هندسي
To prove a geometric shape is the correct locus for a given set of conditions, one generally divides the proof into two stages:[1]
- Proof that all the points that satisfy the conditions are on the given shape.
- Proof that all the points on the given shape satisfy the conditions.
أمثلة
المثال الأول
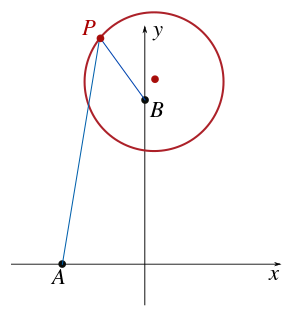
Find the locus of a point P that has a given ratio of distances k = d1/d2 to two given points.
In this example k = 3, A(−1, 0) and B(0, 2) are chosen as the fixed points.
- P(x, y) is a point of the locus
This equation represents a circle with center (1/8, 9/4) and radius . It is the circle of Apollonius defined by these values of k, A, and B.
المثال الثاني
A triangle ABC has a fixed side [AB] with length c. Determine the locus of the third vertex C such that the medians from A and C are orthogonal.
Choose an orthonormal coordinate system such that A(−c/2, 0), B(c/2, 0). C(x, y) is the variable third vertex. The center of [BC] is M((2x + c)/4, y/2). The median from C has a slope y/x. The median AM has slope 2y/(2x + 3c).
- C(x, y) is a point of the locus
- the medians from A and C are orthogonal
The locus of the vertex C is a circle with center (−3c/4, 0) and radius 3c/4.
المثال الثالث
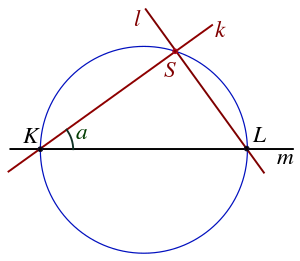
A locus can also be defined by two associated curves depending on one common parameter. If the parameter varies, the intersection points of the associated curves describe the locus.
In the figure, the points K and L are fixed points on a given line m. The line k is a variable line through K. The line l through L is perpendicular to k. The angle between k and m is the parameter. k and l are associated lines depending on the common parameter. The variable intersection point S of k and l describes a circle. This circle is the locus of the intersection point of the two associated lines.
المثال الرابع
A locus of points need not be one-dimensional (as a circle, line, etc.). For example,[2] the locus of the inequality 2x + 3y – 6 < 0 is the portion of the plane that is below the line of equation 2x + 3y – 6 = 0.